傻瓜都看得懂的哈夫曼树

To doubt everything or to believe everything are two equally convenient solutions; both dispense with the necessity of reflection.--------怀疑一切及相信一切都是容易的解决方式， 但是两者都撇除了反思的必要性。

摘要

在数据膨胀、信息爆炸的今天，数据压缩的意义不言而喻。谈到数据压缩，就不能不提哈夫曼（Huffman）编码，哈夫曼编码是首个实用的压缩编码方案，即使在今天的许多知名压缩算法里，依然可以见到哈夫曼编码的影子。

另外，在数据通信中，用二进制给每个字符进行编码时不得不面对的一个问题是如何使电文总长最短且不产生二义性。根据字符出现频率，利用赫夫曼编码可以构造出一种不等长的二进制，使编码后的电文长度最短，且保证不产生二义性。

关键词：二叉树 哈夫曼树 哈夫曼编码 贪心算法

1 背景知识回顾

学习数据结构或者通信方面的知识，哈夫曼编码是不得不提的东西，实现哈夫曼编码前，先介绍哈夫曼树，哈夫曼树又叫最优二叉树。下面我们回顾一下几个关于树的知识点。

1.1 权，路径长度，带权路径长度

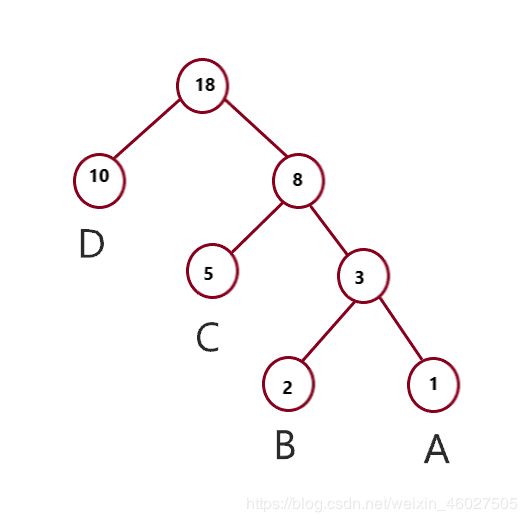
上图给出就是已经构造好的{A,B,C,D}对印的哈夫曼树，下面会讲述如何构造，我们先通过这个树讲解几个概念。

• (1) 路径长度：就是从根节点到自己节点之间的直线的数目， 比如A节点的路径长度就是3，C节点的路径长度是2， D节点的路径长度就是1。
  若规定根节点的层数是1， 那么第L层节点的路径长度就是L-1;
• (2) 权： 若将树中的节点赋给一个有着某种含义的数值，则这个数值称为该节点的权。例如：A节点的权就是1。
• (3) 节点的带权路径长度 = 该节点的路径长度 * 该节点的权
  例如： B的带权路径长度 = 3 * 2 = 6；
• (4) 树的带权路径长度(WPL) :所有叶子节点的带权路径长度之和。

例如：上面哈夫曼树WPL = 1 * 10 + 2 * 5 +3 * 2 +1* 3 = 29
WPL越小，说明构造出来的二叉树性能就越优

1.2 啥是哈夫曼树

• 定义：给定n个权值作为n个叶子节点，构成一颗二叉树，若树的WPL(带权路径长度)达到最小，这棵树就是哈夫曼树。

下面我们验证一下，画一个以上面4个叶子节点构造的另外一棵二叉树，计算WPL,比较一下，看看是不是哈夫曼的WPL更小。

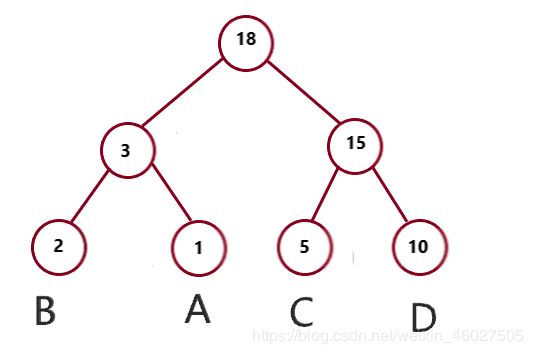
WPL = 2*(2+1+5+10)= 36
显然大于哈夫曼的WPL

1.3 如何通过哈夫曼树编码

我们还是以上面的哈夫曼树为例子，其中的现实意义是：

假如我们要发送ACCCCCBBDDDDDDDDDD这样的电文，那我们如何编码，如果使用定长编码的话就是：

A(00) B(01) C(10) D(11)

但是这样编码，D比A出现的频率大得多，但是却占用相同的位数空间，显然造成了空间的严重浪费，

所以我们引进哈夫曼编码(不定长编码)，根据字符出现的频率来编码。

上面A出现1次，B出现2次，C出现5次，D出现10次，这个次数就是节点的权值。

如何构造哈夫曼树，在后面的设计流程会介绍。

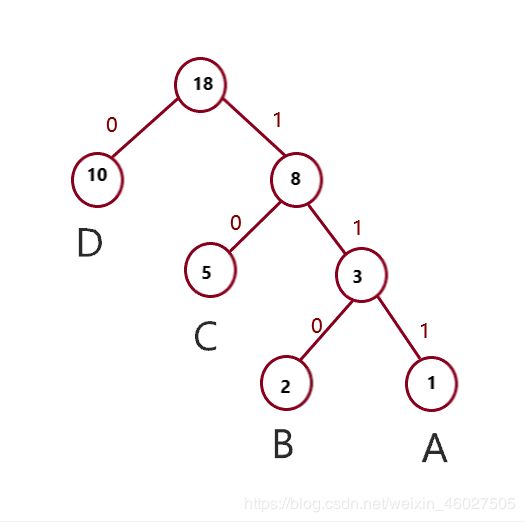
然后我们将构造好的哈夫曼树，节点到其左孩子的路径标为0，到右孩子的路径标为1.

然后组合路径上的编码就得到了哈夫曼编码。
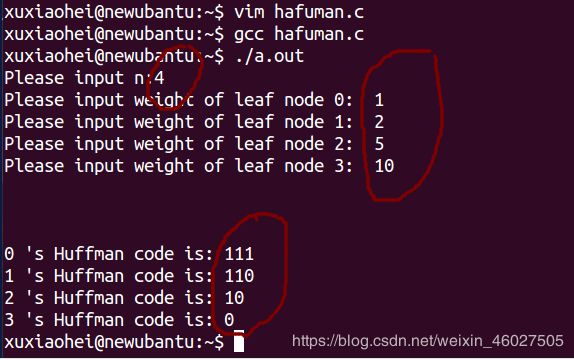
A(111) B(110) C(10) D(0)

2 设计思想

哈夫曼的编码效率相当高，对信源的统计特性没有特殊要求，对编码设备的要求也比较简单，综合性能都优于香农编码和费诺编码。
其实设计哈夫曼编码的思想就是贪心算法，选择当前对自己最优的方案。

3 设计流程

那上面的哈夫曼树是怎么构造出来的呢？
下面我们换个复杂的例子，发送由A,B,C,D,E 5个字符组成的电文，然后权值(即出现次数)分别是{5， 6， 7，8，15}
将上面这个集合当作第一个步骤的集合。
在下图中就是挂在直线上的第一排节点。

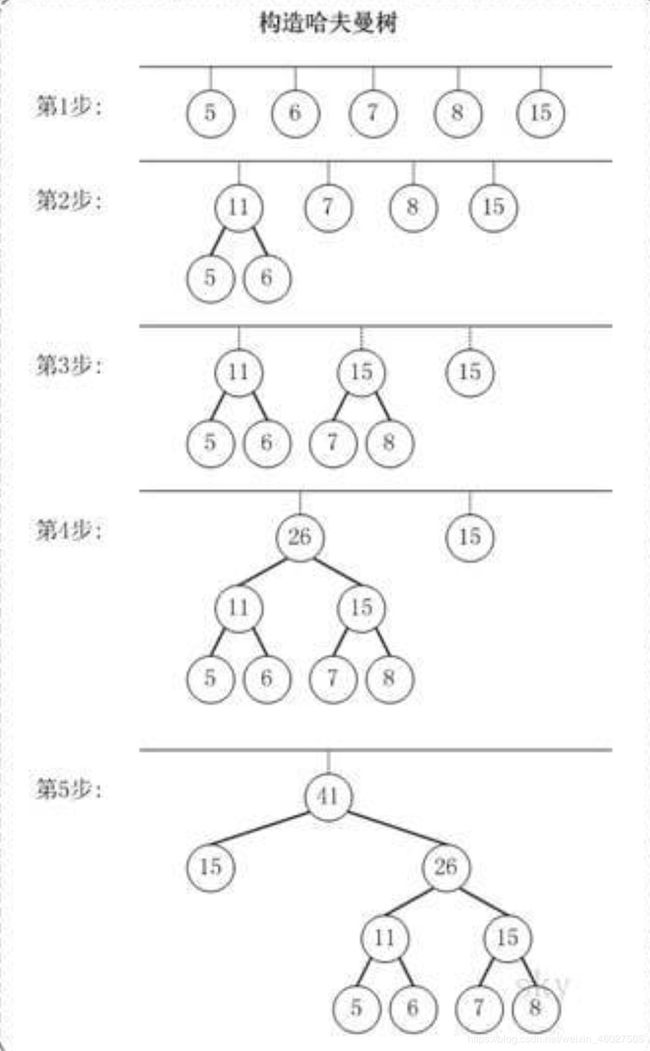
第一步： 创建森林(集合)，包括{5，6，7，8，15}
第二步： 在集合中取权值最小的两个权值相加得到新的节点，然后将新节点加入到集合中，然后原来的两个节点分别成为新节点的左右孩子。这时集合变为{11，7，8，15}
第三步： 同样的步骤，取新的集合中最小的两个生成新的集合{11，15，15}，下面的孩子节点我们可以假装看不见，只用管新的集合就行了。
第四步： 重复上述步骤
第五步： 就得到了哈夫曼树。
第六步： 在路径上标上0和1，就得到了A(100) B(101) C(110) D(111) E(0)

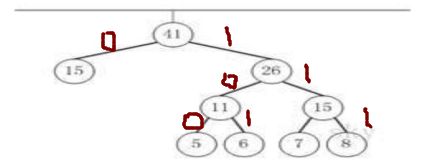
4 设计程序

/*********************************************************************************
 *      Copyright:  (C) 2020 BIG WORLD
 *                  All rights reserved.
 *
 *       Filename:  hafuman.c
 *    Description:  This file 
 *                 徐鑫桦 通信1702 201721112066
 *        Version:  1.0.0(2020年04月28日)
 *         Author:  xuxiaohei徐鑫桦 <[email protected]>
 *      ChangeLog:  1, Release initial version on "2020年04月28日 15时43分34秒"
 *                 
 ********************************************************************************/
#include 

#define MAXBIT      100
#define MAXVALUE  10000
#define MAXLEAF     30
#define MAXNODE    MAXLEAF*2 -1

typedef struct
{
    int bit[MAXBIT];
    int start;
} HCodeType;        /* 编码结构体 */


typedef struct
{
    int weight;
    int parent;
    int lchild;
    int rchild;
} HNodeType;        /* 结点结构体 */


/* 构造一颗哈夫曼树 */
void HuffmanTree (HNodeType HuffNode[MAXNODE],  int n)
{
    /* i、j： 循环变量，m1、m2：构造哈夫曼树不同过程中两个最小权值结点的权值，
        x1、x2：构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/
    int i, j, m1, m2, x1, x2;
    /* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */
    for (i=0; i<2*n-1; i++)
    {
        HuffNode[i].weight = 0;
        HuffNode[i].parent =-1;
        HuffNode[i].lchild =-1;
        HuffNode[i].lchild =-1;
    } /* end for */

    /* 输入 n 个叶子结点的权值 */
    for (i=0; i<n; i++)
    {
        printf ("Please input weight of leaf node %d:  ", i);
        scanf ("%d", &HuffNode[i].weight);
    } /* end for */

    /* 循环构造 Huffman 树 */
    for (i=0; i<n-1; i++)
    {
        m1=m2=MAXVALUE;     /* m1、m2中存放两个无父结点且结点权值最小的两个结点 */
        x1=x2=0;
        /* 找出所有结点中权值最小、无父结点的两个结点，并合并之为一颗二叉树 */
        for (j=0; j<n+i; j++)
        {
            if (HuffNode[j].weight < m1 && HuffNode[j].parent==-1)
            {
                m2=m1;
                x2=x1;
                m1=HuffNode[j].weight;
                x1=j;
            }
            else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1)
            {
                m2=HuffNode[j].weight;
                x2=j;
            }
        } /* end for */
            /* 设置找到的两个子结点 x1、x2 的父结点信息 */
        HuffNode[x1].parent  = n+i;
        HuffNode[x2].parent  = n+i;
        HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;
        HuffNode[n+i].lchild = x1;
        HuffNode[n+i].rchild = x2;

      //  printf ("x1.weight and x2.weight in round %d: %d, %d\n", i+1, HuffNode[x1].weight, HuffNode[x2].weight);  /* 用于测试 */
        printf ("\n");
    } /* end for */
} /* end HuffmanTree */

int main(void)
{
    HNodeType HuffNode[MAXNODE];            /* 定义一个结点结构体数组 */
    HCodeType HuffCode[MAXLEAF],  cd;       /* 定义一个编码结构体数组， 同时定义一个临时变量来存放求解编码时的信息 */
    int i, j, c, p, n;
    printf ("Please input n:");
    scanf ("%d", &n);
    HuffmanTree (HuffNode, n);

    for (i=0; i < n; i++)
    {
        cd.start = n-1;
        c = i;
        p = HuffNode[c].parent;
        while (p != -1)   /* 父结点存在 */
        {
            if (HuffNode[p].lchild == c)
                cd.bit[cd.start] = 1;
            else
                cd.bit[cd.start] = 0;
            cd.start--;        /* 求编码的低一位 */
            c=p;
            p=HuffNode[c].parent;    /* 设置下一循环条件 */
        } /* end while */

        /* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */
        for (j=cd.start+1; j<n; j++)
        { HuffCode[i].bit[j] = cd.bit[j];}
        HuffCode[i].start = cd.start;
    } /* end for */

    /* 输出已保存好的所有存在编码的哈夫曼编码 */
    for (i=0; i<n; i++)
    {
        printf ("%d 's Huffman code is: ", i);
        for (j=HuffCode[i].start+1; j < n; j++)
        {
            printf ("%d", HuffCode[i].bit[j]);
        }
        printf ("\n");
    }
    getchar();
    return 0;
}

5 设计结果演示

我们输入第一个例子的权值，得到和理论推演一样的结果，说明程序正确。