【计算机图形学】图元的区域填充之多边形的区域填充

相关资料来源于网络，侵删歉。
如果文章中存在错误，请下方评论告知我，谢谢！

---

多边形的区域填充

首先，我们了解一下多边形。
多边形可以简单地分为凸多边形和凹多边形，除此之外，我们还要讨论内含环的多边形，如下图。

多边形的表示方法
顶点表示：用多边形顶点的序列来刻画多边形。直观、几何意义强、占内存少；不能直接用于显示。
点阵表示：用位于多边形内的像素的集合来刻画多边形。失去了许多重要的几何信息；但它是光栅显示系统显示时所需的表示形式，易于面着色。

多边形的扫描转换（多边形的区域填充）
把多边形的顶点表示转换为点阵表示，也就是从多边形的给定边界出发，求出位于其内部的各个像素，并给各个像素设置相应的灰度和颜色，通常称这种转换为多边形的扫描转换。
方法：逐点判断法，扫描线算法，边缘填充法等。

---

前提
多边形的顶点坐标均为整数。

逐点判断法

逐个判断绘图窗口内的像素，确定是否在多边形区域内，从而求出位于多边形区域内的像素集合。

#define MAXN 100
typedef struct{
	int PolygonNum;//多边形顶点个数
	Point vertexces[MAXN];//多边形顶点数组
}Polygon;

void FillPolygonPbyP(Polygon *P, int color){
	int x, y;
	for(y=ymin;y<=ymax;y++)
	for(x=xmin;x<=xmax;x++)
		if(isInside(P,x,y))
			WritePixel(x,y,color);
}

如何判断点在多边形内外呢？
1.射线法
从点v发出射线，求与多边形的交点个数n。若n为奇数，则点v在多边形内部；若n为偶数，则点v在多边形外部。
2.累计角度法
从点v向多边形的每个顶点发出射线，形成有向角，计算所有有向角的角度和S。若S=0，则点v在多边形外部；若S=±2π，则点v在多边形内部。

逐点判断的算法虽然程序简单，但不可取。原因是速度太慢，主要是由于该算法割断了各象素之间的联系，孤立地考察各象素与多边形的内外关系，使得几十万甚至几百万个象素都要一一判别，每次判别又要多次求交点，需要做大量的乘除运算，花费很多时间。

扫描线算法

前提：处理对象为非自交多边形，即边与边之间除了顶点外无其它交点，如下图是自交多边形。

将多边形填充分解为一条条的扫描线填充（扫描线是纵坐标为整数的横线）。对任一条扫描线，自左向右确定该扫描线与多边形的交点位置，并对每对交点间的像素进行填充。那么关键是如何求扫描线与多边形各边的交点，并进行取舍，如下图。

我们作如下规定：
1.如果交点非整数
交点位于左边之上，向右取整；交点位于右边之上，向左取整。（要使交点位于多边形内）
2.落在右上边界的像素不记录。
3.如果交点是与扫描线相交的那条边的上端点，单独对这条边不记录。（结合上图中2、4、5、6-7间的点加以理解）

步骤
求交：求扫描线与多边形各边交点
排序：按x递增顺序对交点排序
交点匹配：依次每两个交点配对，在上图中(1,2)，(3,4)，(5,6)，(7,8)配对。
填充：填充每对交点间在多边形区域内部的象素。

几点说明
1.交点个数为偶数。
2.若交点个数为n，则配对的点为(k,k+1)，k=1,3,5...,n-1。
3.配对的区间是位于多边形内的，其余不是。

接下来我们具体了解一下如何求扫描线与多边形的交点。

假定已经求解出扫描线y=e和多边形边的所有交点，那么递推出扫描线y=d=e+1与多边形边的交点，求解可分为两类：
1.边既和y=e相交，又和y=d相交。
若x为其中某条边与y=e的交点横坐标，k为该边的斜率，则此边与y=d的交点横坐标x'=x+1/k；
2.边只与y=d相交，不与y=e相交，即新出现的边。
此时，这些边的下端点就是交点，不用计算。    

几种特殊情况
1.不对水平边计算，在预处理阶段将水平边删除。
2.对尖角的处理（即填充区域非常狭窄），扫描线原则上一个元素都不会填充，这时我们需要进行反走样。

好了，我们来看实现。
扫描线算法中采用了灵活的数据结构。
1.边结构

typedef struct  　
{
   　int ymax; // 边的上端点的y值
  　 float x;　// ET表中为边的下端点的x值；AET中为当前扫描线与边的交点的x值
   　float dx; // 单位高度x方向偏移量（即边的斜率的倒数）
   　E * nextEdge ;  // 指向下一条边的指针
}E;

2.边表ET
边表ET的基本元素是边结构，它是按多边形每条边的下端点的y坐标对非水平边进行分类的。边的下端点y坐标值等于i，那么该边就属于第i类。同一类中的边按其下端点的x值(x值相等的，按dx值)增序排列。如下图。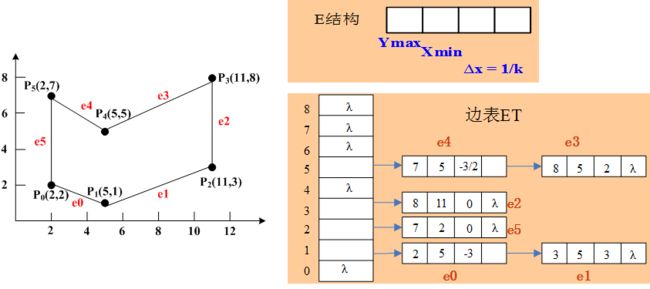

3.活动边表AET
活动边表AET的基本元素也是边结构，它由当前与扫描线相交的边组成，记录多边形的边和当前扫描线的所有交点的x坐标，并且随着扫描线的递增而不断变化。

（边表ET用来排除不必要的求交测试。如求扫描线y=4的AET时，e3,e4所属的类序号5大于4，所以它们和y=4没有交点，不用进行求交测试。）
 

伪代码：

void polyfill (polygon, color)
{  
	//建立全局边表ET;
	for (各条扫描线i )  { 把ymin == i 的边结构－>边表ET [i]  }
	将扫描线i的初值置为ET中非空元素的最小序号；
	初始化活动边表AET为空；
	for (各条扫描线i )
	{
		(1) 把边表ET[i]中的边结点插入AET表;
		(2) 遍历AET表，把y max== i 的结点从AET中删除，并按x坐标值增序排列各边；
		(3) 把配对交点区间(左闭右开)上的象素(x, i)，用WritePixel (x, i, color)改写颜色值；
		(4) 把AET中每条边结点的x值递增△x；
	}
}