Javascript之数据结构与算法的图(Graph)实现
Javascript之数据结构与算法的图(Graph)实现
- 简介
- 广度优先搜索算法实际应用-最短路径(非权值)
- 深度优先搜索算法实际应用-拓扑排序(有向无环图)
- Dijkstra 算法
- Floyd-Warshall 算法
- 最小生成树(MST)-Prim算法
- 全部代码
简介
广度优先搜索算法会从指定的第一个顶点开始遍历图,先访问其所有的相邻点,就像一次访
问图的一层。换句话说,就是先宽后深地访问顶点。如图:

相关代码:
bfs(v,callback){
let color=this.initializeColor();
let adjList=items.get(this).adjList;
let queue=new Queue();
queue.enqueue(v);
while(!queue.empty()){
let u=queue.dequeue();
let neighbors=adjList.get(u);
color[u]='grey';
for(let i=0;i<neighbors.length;i++){
let w=neighbors[i];
if(color[w]=='white'){
color[w]='grey';
queue.enqueue(w);
}
}
color[u]='black';
if(callback){
callback(u);
}
}
}
深度优先搜索将会从第一个指定的顶点开始遍历图,沿着路径直到这条路径最后一个顶
点被访问了,接着原路回退并探索下一条路径。换句话说,它是先深度后广度地访问顶点问所有节点。如图:
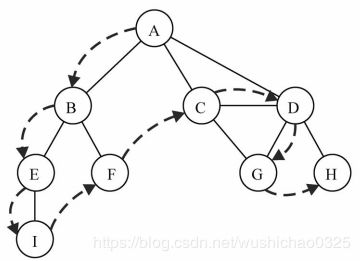
相关代码:
dfs(callback){
let color=this.initializeColor();
let vertices=items.get(this).vertices;
for(let i=0;i<vertices.length;i++){
if(color[vertices[i]]=='white'){
items.get(this).dfsVisit(items.get(this).adjList,items.get(this).dfsVisit,vertices[i],color,callback);
}
}
}
dfsVisit(adjList,dfsVisit,u,color,callback){
color[u]='grey';
if(callback){
callback(u);
}
let neighbors=adjList.get(u);
for(let i=0;i<neighbors.length;i++){
let w=neighbors[i];
if(color[w]=='white'){
dfsVisit(adjList,dfsVisit,w,color,callback);
}
}
color[u]='black';
}
广度优先搜索算法实际应用-最短路径(非权值)
问题背景:
给定一个图G和源顶点v,找出对每个顶点u, u和v之间最短路径的距离(以边的数量计)。
解决办法:
改良bfs算法即BFS:
BFS(v){//-不加权最短路径
let color=this.initializeColor();
let queue=new Queue();
let d=[];//存路径
let pred=[];
queue.enqueue(v);
let vertices=items.get(this).vertices;
let adjList=items.get(this).adjList;
for(let i=0;i<vertices.length;i++){
d[vertices[i]]=0;
pred[vertices[i]]=null;
}
while(!queue.empty()){
let u=queue.dequeue();
let neighbors=adjList.get(u);
color[u]='grey';
for(let i=0;i<neighbors.length;i++){
let w=neighbors[i];
if(color[w]=='white'){
color[w]='grey';
d[w]=d[u]+1;
pred[w]=u;
queue.enqueue(w);
}
}
color[u]='black';
}
return {distances:d,predecessors:pred}
}
测试代码:
var graph = new Graph();
var myVertices = ['A','B','C','D','E','F','G','H','I']; //{7}
for (var i=0; i<myVertices.length; i++){ //{8}
graph.addVertex(myVertices[i]);
}
graph.addEdge('A', 'B'); //{9}
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');
var shortestPathA = graph.BFS(myVertices[0]);
console.log(shortestPathA);
//输出结果:
distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3],
predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E"]
//显示顶点到其他顶点的路径
var fromVertex = myVertices[0];
for (var i=1; i<myVertices.length; i++){
var toVertex = myVertices[i],
path = new Stack();
for (var v=toVertex; v!== fromVertex;v=shortestPathA.predecessors[v]) {
path.push(v);
}
path.push(fromVertex);
var s = path.pop();
while (!path.isEmpty()){
s += ' - ' + path.pop();
}
console.log(s);
}
深度优先搜索算法实际应用-拓扑排序(有向无环图)
编排一些任务或步骤的执行顺序时,这称为拓扑排序
例如:
当我们开始学习一门计算机科学课程,在学习某些知识之前得按顺序完成一些知识储备(你不可以在上算法前先上算法)。当我们在开发一个项目时,需要按顺序执行一些步骤,例如,首先我们得从客户那里得到需求,接着开发客户要求的东西,最后交付项目。
解决办法:
改良版dfs即DFS:
DFS(){
let color=this.initializeColor();
let d=[];
let f=[];
let p=[];
items.get(this).time=0;
let vertices=items.get(this).vertices;
for(let i=0;i<vertices.length;i++){
f[vertices[i]]=0;
d[vertices[i]]=0;
p[vertices[i]]=null;
}
for(let i=0;i<vertices.length;i++){
if(color[vertices[i]]=='white'){
items.get(this).DFSVisit(items.get(this).time,items.get(this).adjList,items.get(this).DFSVisit,vertices[i],color,d,f,p);
}
}
return {
discovered:d,
finished:f,
predecessors:p
}
}
Dijkstra 算法
Dijkstra算法是一种计算从单个源到所有其他源的最短路径的贪心算法。
例如:

将图上信息转化为邻接矩阵:
graph.graph = [[0, 2, 4, 0, 0, 0],
[2, 0, 2, 4, 2, 0],
[4, 2, 0, 0, 3, 0],
[0, 4, 0, 0, 3, 2],
[0, 2, 3, 3, 0, 2],
[0, 0, 0, 2, 2, 0]];
相关代码:
//Dijkstra算法
dijkstra(src){
let dist=[];
let INF=Number.MAX_SAFE_INTEGER;
let visited=[];
let length=this.graph.length;
for(let i=0;i<length;i++){//把所有的距离( dist)初始化为无限大( JavaScript最大的数INF = Number.MAX_SAFE_INTEGER),将visited[]初始化为false
dist[i]=INF;
visited[i]=false;
}
dist[src]=0;//把源顶点到自己的距离设为0
for(let i=0;i<length-1;i++){
let u=items.get(this).minDistance(dist,visited);//从尚未处理的顶点中选出距离最近的顶点
visited[u]=true;//把选出的顶点标为visited,以免重复计算
for(let v=0;v<length;v++){//查找更短的路径
if(!visited[v]&&this.graph[u][v]!=0&&dist[u]!=INF&&dist[u]+this.graph[u][v]<dist[v]){
dist[v]=dist[u]+this.graph[u][v];//更新最短路径的值
}
}
}
return dist;
}
minDistance(dist,visited){
let INF=Number.MAX_SAFE_INTEGER;
let min=INF;
let minIndex=-1;
for(let v=0;v<dist.length;v++){
if(visited[v]==false&&dist[v]<=min){
min=dist[v];
minIndex=v;
}
}
return minIndex;
}
Floyd-Warshall 算法
Floyd-Warshall算法是一种计算图中所有最短路径的动态规划算法
//Floyd-Warshall算法
floydWarshall(){
let INF=Number.MAX_SAFE_INTEGER;
let dist=[],
length=this.graph.length;
for(let i=0;i<length;i++){//首先,把dist数组初始化为每个顶点之间的权值,因为i到j可能的最短距离就是这些顶点间的权值。
dist[i]=[];
for(let j=0;j<length;j++){
if(this.graph[i][j]==0&&i!=j){
dist[i][j]=INF;
}else{
dist[i][j]=this.graph[i][j];
}
}
}
for(let k=0;k<length;k++){//通过k,得到i途径顶点0至k,到达j的最短路径。
for(let i=0;i<length;i++){
for(let j=0;j<length;j++){
if(dist[i][k]+dist[k][j]<dist[i][j]){//通过k,得到i途径顶点0至k,到达j的最短路径。
dist[i][j]=dist[i][k]+dist[k][j];//如果是更短的路径,则更新最短路径的值
}
}
}
}
return dist;
}
最小生成树(MST)-Prim算法
实用背景:
你的公司有几间办公室,要以最低的成本实现办公室电话线路相互连通,以节省资金;
在n个岛屿之间建造桥梁,想用最低的成本实现所有岛屿相互连通。
图结构如下:

Prim算法是一种求解加权无向连通图的MST问题的贪心算法。它能找出一个边的子集,使得
其构成的树包含图中所有顶点,且边的权值之和最小。
相关代码:
prim(){
let parent=[],
key=[],
visited=[],
length=this.graph.length,
INF=Number.MAX_SAFE_INTEGER;//代表无穷大即无路
for(let i=0;i<this.graph.length;i++){
for(let j=0;j<this.graph[i].length;j++){
if(this.graph[i][j]==0&&i!=j){
this.graph[i][j]=INF;
}
}
}
for(let i=0;i<length;i++){
key[i]=INF;
visited[i]=false;
}
key[0]=0;
parent[0]=-1;//选择第一个key作为第一个顶点,同时,因为第一个顶点总是MST的根节点,所以parent[0] = -1。
for(let i=0;i<length-1;i++){
let u=items.get(this).minKey(key,visited);//从未处理的顶点集合中选出key值最小的顶点(与Dijkstra算法中使用的函数一样,只是名字不同)
visited[u]=true;
for(let v=0;v<length;v++){
if(this.graph[u][v]&&visited[v]==false&&this.graph[u][v]<key[v]){
parent[v]=u;
key[v]=this.graph[u][v];
}
}
}
//console.log(key)
return {
parent:parent,
key:key
};
}
全部代码
let Dictionary=require('./Dictionary')
let Queue=require('./Queue')
let Stack=require('./Stack')
let items=new WeakMap();
/**
* 白色:表示该顶点还没有被访问。
* 灰色:表示该顶点被访问过,但并未被探索过。
* 黑色:表示该顶点被访问过且被完全探索过
*/
class Graph{
constructor(){
items.set(this,{
"vertices":[],
"adjList":new Dictionary(),
"time":0,
"dfsVisit":function(adjList,dfsVisit,u,color,callback){
color[u]='grey';
if(callback){
callback(u);
}
let neighbors=adjList.get(u);
for(let i=0;i<neighbors.length;i++){
let w=neighbors[i];
if(color[w]=='white'){
dfsVisit(adjList,dfsVisit,w,color,callback);
}
}
color[u]='black';
},
"DFSVisit":function(time,adjList,DFSVisit,u,color,d,f,p){
console.log('discovered '+u);
color[u]='grey';
d[u]=++time;
let neighbors=adjList.get(u);
for(let i=0;i<neighbors.length;i++){
let w=neighbors[i];
if(color[w]=='white'){
p[w]=u;
DFSVisit(time,adjList,DFSVisit,w,color,d,f,p);
}
}
color[u]='black';
f[u]=++time;
console.log('explored '+u);
},
"minDistance":function(dist,visited){
let INF=Number.MAX_SAFE_INTEGER;
let min=INF;
let minIndex=-1;
for(let v=0;v<dist.length;v++){
if(visited[v]==false&&dist[v]<=min){
min=dist[v];
minIndex=v;
}
}
return minIndex;
},
"minKey":function(key,visited){
let INF=Number.MAX_SAFE_INTEGER;
let min=INF;
let minIndex=-1;
for(let v=0;v<key.length;v++){
if(visited[v]==false&&key[v]<=min){
min=key[v];
minIndex=v;
}
}
return minIndex;
}
});//私有属性
this.graph=[];//dijkstra算法使用
}
addVertex(v){
items.get(this).vertices.push(v);
items.get(this).adjList.set(v,[]);
}
addEdge(v,w){
items.get(this).adjList.get(v).push(w);
items.get(this).adjList.get(w).push(v);
}
toString(){
let s='';
let vertices=items.get(this).vertices;
for(let i=0;i<vertices.length;i++){
s+=vertices[i]+'->';
let neighbors=items.get(this).adjList.get(vertices[i])
for(let j=0;j<neighbors.length;j++){
s+=neighbors[j]+' ';
}
s+='\n';
}
return s;
}
//初始化节点颜色
initializeColor(){
let color=[];
let vertices=items.get(this).vertices;
for(let i=0;i<vertices.length;i++){
color[vertices[i]]='white';
}
return color;
}
//广度优先搜索
bfs(v,callback){
let color=this.initializeColor();
let adjList=items.get(this).adjList;
let queue=new Queue();
queue.enqueue(v);
while(!queue.empty()){
let u=queue.dequeue();
let neighbors=adjList.get(u);
color[u]='grey';
for(let i=0;i<neighbors.length;i++){
let w=neighbors[i];
if(color[w]=='white'){
color[w]='grey';
queue.enqueue(w);
}
}
color[u]='black';
if(callback){
callback(u);
}
}
}
BFS(v){//-不加权最短路径
let color=this.initializeColor();
let queue=new Queue();
let d=[];//存路径
let pred=[];
queue.enqueue(v);
let vertices=items.get(this).vertices;
let adjList=items.get(this).adjList;
for(let i=0;i<vertices.length;i++){
d[vertices[i]]=0;
pred[vertices[i]]=null;
}
while(!queue.empty()){
let u=queue.dequeue();
let neighbors=adjList.get(u);
color[u]='grey';
for(let i=0;i<neighbors.length;i++){
let w=neighbors[i];
if(color[w]=='white'){
color[w]='grey';
d[w]=d[u]+1;
pred[w]=u;
queue.enqueue(w);
}
}
color[u]='black';
}
return {distances:d,predecessors:pred}
}
//深度优先搜索
dfs(callback){
let color=this.initializeColor();
let vertices=items.get(this).vertices;
for(let i=0;i<vertices.length;i++){
if(color[vertices[i]]=='white'){
items.get(this).dfsVisit(items.get(this).adjList,items.get(this).dfsVisit,vertices[i],color,callback);
}
}
}
//探索深度优先算法
DFS(){
let color=this.initializeColor();
let d=[];
let f=[];
let p=[];
items.get(this).time=0;
let vertices=items.get(this).vertices;
for(let i=0;i<vertices.length;i++){
f[vertices[i]]=0;
d[vertices[i]]=0;
p[vertices[i]]=null;
}
for(let i=0;i<vertices.length;i++){
if(color[vertices[i]]=='white'){
items.get(this).DFSVisit(items.get(this).time,items.get(this).adjList,items.get(this).DFSVisit,vertices[i],color,d,f,p);
}
}
return {
discovered:d,
finished:f,
predecessors:p
}
}
//Dijkstra算法
dijkstra(src){
let dist=[];
let INF=Number.MAX_SAFE_INTEGER;
let visited=[];
let length=this.graph.length;
for(let i=0;i<length;i++){//把所有的距离( dist)初始化为无限大( JavaScript最大的数INF = Number.MAX_SAFE_INTEGER),将visited[]初始化为false
dist[i]=INF;
visited[i]=false;
}
dist[src]=0;//把源顶点到自己的距离设为0
for(let i=0;i<length-1;i++){
let u=items.get(this).minDistance(dist,visited);//从尚未处理的顶点中选出距离最近的顶点
visited[u]=true;//把选出的顶点标为visited,以免重复计算
for(let v=0;v<length;v++){//查找更短的路径
if(!visited[v]&&this.graph[u][v]!=0&&dist[u]!=INF&&dist[u]+this.graph[u][v]<dist[v]){
dist[v]=dist[u]+this.graph[u][v];//更新最短路径的值
}
}
}
return dist;
}
//Floyd-Warshall算法
floydWarshall(){
let INF=Number.MAX_SAFE_INTEGER;
let dist=[],
length=this.graph.length;
for(let i=0;i<length;i++){//首先,把dist数组初始化为每个顶点之间的权值,因为i到j可能的最短距离就是这些顶点间的权值。
dist[i]=[];
for(let j=0;j<length;j++){
if(this.graph[i][j]==0&&i!=j){
dist[i][j]=INF;
}else{
dist[i][j]=this.graph[i][j];
}
}
}
for(let k=0;k<length;k++){//通过k,得到i途径顶点0至k,到达j的最短路径。
for(let i=0;i<length;i++){
for(let j=0;j<length;j++){
if(dist[i][k]+dist[k][j]<dist[i][j]){//通过k,得到i途径顶点0至k,到达j的最短路径。
dist[i][j]=dist[i][k]+dist[k][j];//如果是更短的路径,则更新最短路径的值
}
}
}
}
return dist;
}
//最小生成树
//Prim算法
prim(){
let parent=[],
key=[],
visited=[],
length=this.graph.length,
INF=Number.MAX_SAFE_INTEGER;
for(let i=0;i<this.graph.length;i++){
for(let j=0;j<this.graph[i].length;j++){
if(this.graph[i][j]==0&&i!=j){
this.graph[i][j]=INF;
}
}
}
for(let i=0;i<length;i++){
key[i]=INF;
visited[i]=false;
}
key[0]=0;
parent[0]=-1;//选择第一个key作为第一个顶点,同时,因为第一个顶点总是MST的根节点,所以parent[0] = -1。
for(let i=0;i<length-1;i++){
let u=items.get(this).minKey(key,visited);//从未处理的顶点集合中选出key值最小的顶点(与Dijkstra算法中使用的函数一样,只是名字不同)
visited[u]=true;
for(let v=0;v<length;v++){
if(this.graph[u][v]&&visited[v]==false&&this.graph[u][v]<key[v]){
parent[v]=u;
key[v]=this.graph[u][v];
}
}
}
//console.log(key)
return {
parent:parent,
key:key
};
}
}
let graph=new Graph();
// let myVertices=['A','B','C','E','D','F','G','H','I'];
// for(let i=0;i
// graph.addVertex(myVertices[i]);
// }
// graph.addEdge('A', 'B'); //{9}
// graph.addEdge('A', 'C');
// graph.addEdge('A', 'D');
// graph.addEdge('C', 'D');
// graph.addEdge('C', 'G');
// graph.addEdge('D', 'G');
// graph.addEdge('D', 'H');
// graph.addEdge('B', 'E');
// graph.addEdge('B', 'F');
// graph.addEdge('E', 'I');
// console.log(graph.toString())
// graph.bfs(myVertices[0],function(result){
// console.log('Visited vertex:',result)
// })
// let shortestPathA=graph.BFS(myVertices[0]);
// console.log(shortestPathA)
// let fromVertex=myVertices[0];
// for(let i=1;i
// let toVertex=myVertices[i];
// let path=new Stack();
// for(let v=toVertex;v!=fromVertex;v=shortestPathA.predecessors[v]){
// path.push(v);
// }
// path.push(fromVertex);
// let s=path.pop();
// while(!path.empty()){
// s+='-'+path.pop();
// }
// console.log(s)
// }
// graph.dfs(function(result){
// console.log('visited vertex:',result)
// })
//拓扑排序
// let myVertices=['A','B','C','D','E','F'];
// for(let i=0;i
// graph.addVertex(myVertices[i]);
// }
// graph.addEdge('A', 'C');
// graph.addEdge('A', 'D');
// graph.addEdge('B', 'D');
// graph.addEdge('B', 'E');
// graph.addEdge('C', 'F');
// graph.addEdge('F', 'E');
// var result = graph.DFS();
// console.log(result)
//dijkstra算法
// graph.graph=[[0, 2, 4, 0, 0, 0],
// [0, 0, 1, 4, 2, 0],
// [0, 0, 0, 0, 3, 0],
// [0, 0, 0, 0, 0, 2],
// [0, 0, 0, 3, 0, 2],
// [0, 0, 0, 0, 0, 0]];
//console.log(graph.dijkstra(0))
//floyd-warshall算法
//console.log(graph.floydWarshall());
//prim
graph.graph = [[0, 2, 4, 0, 0, 0],
[2, 0, 2, 4, 2, 0],
[4, 2, 0, 0, 3, 0],
[0, 4, 0, 0, 3, 2],
[0, 2, 3, 3, 0, 2],
[0, 0, 0, 2, 2, 0]];
let json=graph.prim();
console.log("Edge\t"+"Weight");
let key=json.key;
let parent=json.parent;
for(let i=1;i<key.length;i++){
console.log(parent[i]+"-"+i+"\t"+key[i]);
}