采样定理的说明
看到一篇写的不错的博文,转载收藏。原文链接http://blog.sina.com.cn/s/blog_64c161a00100hqkw.html 如下:
下面是我在网上找的一些关于采样定理的表述:
**************************************************************************************************
在进行模拟/数字信号的转换过程中,当采样频率fs.max大于信号中,最高频率fmax的2倍时,fs.max>=2fmax,则采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的5~10倍;采样定理又称奈奎斯特定理。
当对一个信号进行采样时, 采样频率必须大于该信号带宽的两倍以上才能确保从采样值完全重构原来的信号。
**************************************************************************************************
以上表述都提到了信号采样频率满足条件可以保留信号的完整信息,那么这个“信息”指的是什么呢?图1是我用Matlab模拟10Hz正弦信号在不同采样频率下获得的波形。 图1
显然对一个正弦信号,一个周期仅采集几个点是不能完全还原原来的波形的,当采样频率>9f 时,波形较平滑。
图2、图3是以频率为5Hz、10Hz,在不同的采样频率下,用Matlab画的波形及FFT频谱。

图2
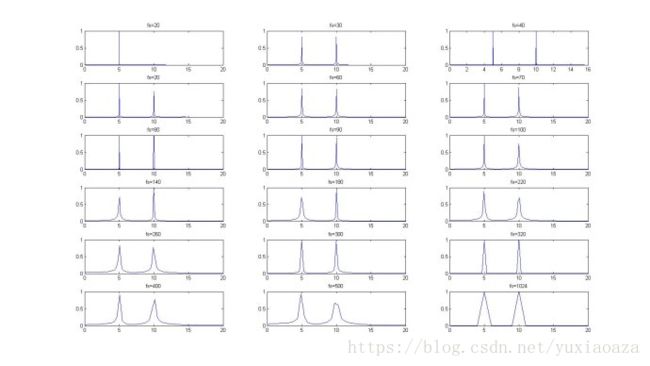
图3
可以看出要还原波形,采样频率仅仅满足采样定理是不够的,但从FFT频谱图上可以看出,只要采样频率“大于”信号最大频率,是可以得到信号的完整信息的(幅值、相位、频率),这里特别强调是“大于”,而不是“>=”,如图3所示,fs=20Hz时在频谱图上是没有10Hz的信息,证明一个事情是正确很难,但证明错误的只要有一个反例就够了,所以采样定理的表述应当是“>”而不是“>=”,程佩青编《数字信号处理教程》(这是我看的第一本信号处理方面的书)描述采样定理时就用的“>”。所以教科书上的东西要比网站上描述的东西要严谨些。
综上,采样定理所要说的是避免信号在频域出现混叠失真的一个最基本条件,而不是时域信号不失真的条件,一些PPT课件,或者老师常常误导我们,如果我们要获得波形的原始信号的话,采样定理的最跟本条件是不能满足需要的。
我们可以接着这个话题继续说下去,既然采样频率大可以获得良好的波形,那么是不是采样频率越大越好呢?显然不是,从图3可以看出,当采样频率较大时,波形的谱线范围也变宽了,且频率分辨率也增大了,因为频率分辨率满足:
Δf=fs/N
一味的增大采样频率是不会获得好的频率分辨率的,要获得好的频率分辨率,相应的要增大采样点数N。我在以前遇到过这种情况,某公司把自己研发的机组状态监测设备向我们展示,说每周期采样128点,即采样频率为128倍转频,目的是说明他们的设备先进,因为我目前用的设备是每周期采32点,他们这套说辞只能糊弄外行,因为他们的设备没增加采样点数,针对我们10000多转速的压缩机,他们频率分辨率是20Hz多,连50Hz的频率都发现不了,这样的监测设备是不能用在故障分析上的。
前些天某公司的人还说他们的设备要做到1600谱线,给人感觉很厉害,因为我们目前使用的监测设备是400谱线的,明理人都知道采样点数决定谱线数,谱线数与采样点数的关系是:
采样点数=2.56*谱线数
谱线数1600线是400线的4倍,运算次数只考虑FFT((N/2)*log2(N))就是原来的4.8倍,不知道这个因素他是否考虑过。。。
故障诊断中既要求获得良好的时域信号的波形,又要得到理想的频域分辨率,实际的数采仪实际上是能将二者结合的很好的。满足故障分析的需要,但信号处理作为故障诊断的基础知识,我们也要牢牢掌握,不能太外行了。
下面是我在网上找的一些关于采样定理的表述:
**************************************************************************************************
采样定理指的是,采样频率要大于信号最高频率的2倍,才能无失真的保留信号的完整信息。
在进行模拟/数字信号的转换过程中 当采样频率fs不小于信号中最高频率fmax的2倍 即 fs>=2fmax 时 采样之后的数字信号完整地保留了原始信号中的信息。在进行模拟/数字信号的转换过程中,当采样频率fs.max大于信号中,最高频率fmax的2倍时,fs.max>=2fmax,则采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的5~10倍;采样定理又称奈奎斯特定理。
当对一个信号进行采样时, 采样频率必须大于该信号带宽的两倍以上才能确保从采样值完全重构原来的信号。
**************************************************************************************************
以上表述都提到了信号采样频率满足条件可以保留信号的完整信息,那么这个“信息”指的是什么呢?图1是我用Matlab模拟10Hz正弦信号在不同采样频率下获得的波形。 图1
显然对一个正弦信号,一个周期仅采集几个点是不能完全还原原来的波形的,当采样频率>9f 时,波形较平滑。
图2、图3是以频率为5Hz、10Hz,在不同的采样频率下,用Matlab画的波形及FFT频谱。

图2

图3
可以看出要还原波形,采样频率仅仅满足采样定理是不够的,但从FFT频谱图上可以看出,只要采样频率“大于”信号最大频率,是可以得到信号的完整信息的(幅值、相位、频率),这里特别强调是“大于”,而不是“>=”,如图3所示,fs=20Hz时在频谱图上是没有10Hz的信息,证明一个事情是正确很难,但证明错误的只要有一个反例就够了,所以采样定理的表述应当是“>”而不是“>=”,程佩青编《数字信号处理教程》(这是我看的第一本信号处理方面的书)描述采样定理时就用的“>”。所以教科书上的东西要比网站上描述的东西要严谨些。
综上,采样定理所要说的是避免信号在频域出现混叠失真的一个最基本条件,而不是时域信号不失真的条件,一些PPT课件,或者老师常常误导我们,如果我们要获得波形的原始信号的话,采样定理的最跟本条件是不能满足需要的。
我们可以接着这个话题继续说下去,既然采样频率大可以获得良好的波形,那么是不是采样频率越大越好呢?显然不是,从图3可以看出,当采样频率较大时,波形的谱线范围也变宽了,且频率分辨率也增大了,因为频率分辨率满足:
Δf=fs/N
一味的增大采样频率是不会获得好的频率分辨率的,要获得好的频率分辨率,相应的要增大采样点数N。我在以前遇到过这种情况,某公司把自己研发的机组状态监测设备向我们展示,说每周期采样128点,即采样频率为128倍转频,目的是说明他们的设备先进,因为我目前用的设备是每周期采32点,他们这套说辞只能糊弄外行,因为他们的设备没增加采样点数,针对我们10000多转速的压缩机,他们频率分辨率是20Hz多,连50Hz的频率都发现不了,这样的监测设备是不能用在故障分析上的。
前些天某公司的人还说他们的设备要做到1600谱线,给人感觉很厉害,因为我们目前使用的监测设备是400谱线的,明理人都知道采样点数决定谱线数,谱线数与采样点数的关系是:
采样点数=2.56*谱线数
谱线数1600线是400线的4倍,运算次数只考虑FFT((N/2)*log2(N))就是原来的4.8倍,不知道这个因素他是否考虑过。。。
故障诊断中既要求获得良好的时域信号的波形,又要得到理想的频域分辨率,实际的数采仪实际上是能将二者结合的很好的。满足故障分析的需要,但信号处理作为故障诊断的基础知识,我们也要牢牢掌握,不能太外行了。
