TensorFlow学习(2)——线性回归、训练和损失
线性回归
很多数学不是太好的同学一听到线性回归这么高级的名词往往望而却步,很多东西只要深入学习并没有看起来那么可怕。
那么何为线性回归呢?其实就是我们初中学到的直线方程,还记得不?记不起来也不要紧,瞄一眼下图你必能唤回当年那痛苦的记忆!哈哈

没想到吧,当年最讨厌数学的我,以为买菜用不到那么多数学知识,现在居然用到了。那么这么一条直线方程跟我们机器学习有什么关系呢?
假设我们要分析蟋蟀的鸣叫声与温度的关系,经过昼夜不停的记录,我们制作了下图:
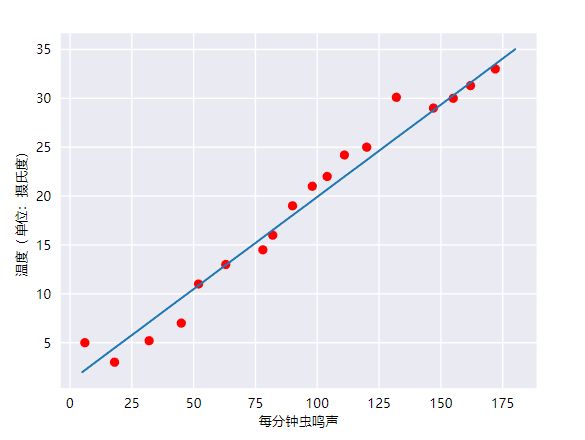
注意观察红点的分布,并做一条线,看起来特别像一条直线方程有木有?虽然不是那么完美。
我们把这种分布叫做线性回归,那么也就是说直线方程现在有了一个更吊的名字叫线性回归。
既然分布没有那么完美,那么我们也应该做出一个不怎么完美的线性回归方程:
y ′ = b + w 1 x 1 y' = b + w_1x_1 y′=b+w1x1
上面的方程只考虑了一个特征值“温度”,如果还有别的特征值呢?比如白天/黑夜、雨天/晴天等,那么该方程又可以继续引入其他变量:
y ′ = b + w 1 x 1 + w 2 x 2 + w 3 x 3 y' = b + w_1x_1 + w_2x_2 + w_3x_3 y′=b+w1x1+w2x2+w3x3
w w w表示什么呢?其实不难,就是表示权重百分比,表示该特征值得重要程度。比如晴天和雨天这个因素对于蟋蟀鸣叫的影响大不?大的话就把 w w w值设置大一点,小的话就设置小一点。
其实上面的方程还可以变得更吊一点,那就是用一个更简练的符号来表示:
y ′ = ∑ i = 0 n w x y'=\sum_{i=0}^nwx y′=∑i=0nwx
有同学可能会问,b 去哪里了?让学弟告诉你吧,其实 b 相当于 x=0 ,这样是为什么 i 的下标会从0开始的原因。
上面的式子虽然看起来更简练了,但是对于我等数学小白来说就变得更加难以理解了,不过数学家喜欢这样,我们要从善如流啊!
训练
首先为什么要训练?仔细观察这个方程 y ′ = b + w 1 x 1 y' = b + w_1x_1 y′=b+w1x1 你会发现在我们的训练数据中, x 1 和 y ′ 都 是 已 知 的 x_1和y'都是已知的 x1和y′都是已知的,但是 w 1 w_1 w1和 b 却是未知的,所以我们训练的目的就是为了确定 w 1 w_1 w1和 b 的值。
损失
如上图所示,所谓的损失就是预测值与真实值之间的差距,上图中红色箭头表示损失。
那么如何测量损失的大小呢?这里有两个方法:
平方损失
所谓的平方损失就是用每个样本的真实值减去预测值再平方,即: 平 方 损 失 = ( y − y ′ ) 2 平方损失 = (y - y')^2 平方损失=(y−y′)2
例如当每分钟虫鸣声为126下的时候我们预测温度为26度,但是实际情况是当时的温度为30度,所以平方损失为: ( 30 − 26 ) 2 (30-26)^2 (30−26)2
均方误差 (MSE)
那什么又是均方误差呢?就是各个样本的所有平方损失之和,然后除以样本数量:
M S E = 1 N ∑ ( x , y ) ∈ D ( y − p r e d i c t i o n ( x ) ) 2 MSE = \frac{1}{N} \sum_{(x,y)\in D} (y - prediction(x))^2 MSE=N1∑(x,y)∈D(y−prediction(x))2
其中 prediction(x) 就是平方损失里的 y ′ y' y′
////////////////////////////////////////////////////欢迎交流/////////////////////////////////////////////////////////
欢迎大家加入Q群讨论:463255841
////////////////////////////////////////////////////欢迎交流/////////////////////////////////////////////////////////
