基于FPGA的CORDIC算法的实现(2)
CORDIC算法旋转模式原理介绍及FPGA实现
- 参考文献
- 项目简述
- 旋转模式的推导过程
- MATLAB仿真
- FPGA代码
- 小结
- 总结
参考文献
[1].碎碎思
项目简述
我们上一篇文章已经讲解了CORDIC的向量模式,通过算法的向量模式我们可以计算向量的幅值与相位角,那么通过算法的旋转模式我们可以计算一个角度的正余弦值。两个模式的不同点就是初始条件与终止条件的设置,相同点都是利用坐标旋转来实现的。这篇博客将结合向量模式的推到原理来进一步说明旋转模式的推导过程。
本次实验我们将使用MATLAB与FPGA同时利用CORDIC算法生成正弦波、余弦波,本次实验所用到的软硬件工具如下:
1、VIVADO 2019.1
2、MATLAB 2015b
3、Modelsim 10.7
旋转模式的推导过程
CORDIC算法旋转模式和向量模式都是不停的对坐标进行旋转,不一样的是向量模式我们的角度变化Z的初值是0,目标是为了将纵坐标轴Y的值经过多次旋转之后变成0,然后通过X的最终值可以求解出 x 2 + y 2 \sqrt{x^2+y^2} x2+y2,通过Z的最终值可以求解出 a r c t a n ( y / x ) arctan(y/x) arctan(y/x)。其中包含的数学关系如下:

上面的式子变化由上一篇博客的推导过程我们可以很容易得到。
与向量模式不同,旋转模式的可以求解的两个量是 c o s ( z 0 ) 、 s i n ( z 0 ) cos(z_0)、sin(z_0) cos(z0)、sin(z0),z的初始条件是 z 0 z_0 z0,终止条件是z经过多次旋转之后变成0。然后我们从整体上看可以把 n n n次的旋转看成1次旋转,这次旋转就是相当于对原来的坐标旋转了 z 0 z_0 z0度,所以对应于数学关系如下:
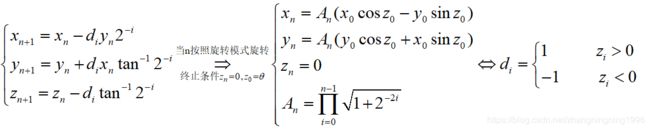
所以只要我们的 x 0 = 0 , y 0 = 1 / A n x_0=0,y_0=1/A_n x0=0,y0=1/An,那么上式就变成了:
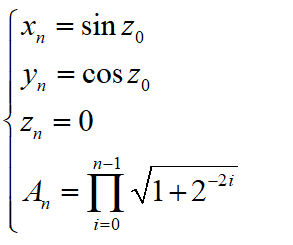
那么我们可以看出经过坐标旋转的初始条件和旋转条件的设置,我们最终可以求解到 c o s ( z 0 ) 、 s i n ( z 0 ) cos(z_0)、sin(z_0) cos(z0)、sin(z0)。这里我们没有对旋转模式情况下的推导过程一步步的讲解,而是结合向量模式下的推导过程,把旋转模式下的n次旋转看成1次旋转一步得到n习次旋转之后的表达式,然后设置初始条件左中可以获得 c o s ( z 0 ) 、 s i n ( z 0 ) cos(z_0)、sin(z_0) cos(z0)、sin(z0)的值。
这里需要特别注意旋转模式与向量模式旋转的角度不一致,旋转模式我们是默认逆时针旋转进行推导,向量模式我们默认是顺时针旋转进行推导。
MATLAB仿真
MATLAB代码如下:
clc;
clear all;
Phase = 0:359;
Phase = [Phase,Phase,Phase];
rot = [2949120;1740992;919872;466944;234368;117312;58688;29312;14656;7360;3648;1856;896;448;256;128];
Pipeline = 16;
K = 39796; %K=0.607253*2^16,32'h09b74,
x = zeros(Pipeline+1,1);
y = zeros(Pipeline+1,1);
z = zeros(Pipeline+1,1);
cose = zeros(length(Phase),1);
sine = zeros(length(Phase),1);
zzz = zeros(length(Phase),1);
for i = 1:length(Phase)
x(1) = K;
y(1) = 0;
if(Phase(i) <= 90)
z(1) = Phase(i)*2^16;
elseif(Phase(i) > 90 && Phase(i) <= 180)
z(1) = (Phase(i)-90)*2^16;
elseif(Phase(i) > 180 && Phase(i) <= 270)
z(1) = (Phase(i)-180)*2^16;
else
z(1) = (Phase(i)-270)*2^16;
end
for j = 1:Pipeline
if(z(j)>0)
x(j+1) = x(j) - floor(y(j)*(2^-(j-1)));
y(j+1) = y(j) + floor(x(j)*(2^-(j-1)));
z(j+1) = z(j) - rot(j);
else
x(j+1) = x(j) + floor(y(j)*(2^-(j-1)));
y(j+1) = y(j) - floor(x(j)*(2^-(j-1)));
z(j+1) = z(j) + rot(j);
end
end
zzz(i) = z(17);
if(Phase(i) <= 90)
cose(i) = x(17);
sine(i) = y(17);
elseif(Phase(i) > 90 && Phase(i) <= 180)
cose(i) = -y(17);
sine(i) = x(17);
elseif(Phase(i) > 180 && Phase(i) <= 270)
cose(i) = -x(17);
sine(i) = -y(17);
else
cose(i) = y(17);
sine(i) = -x(17);
end
end
figure(1)
plot(cose,'r');
hold on
plot(sine,'g');
MATLAB仿真结果如下:
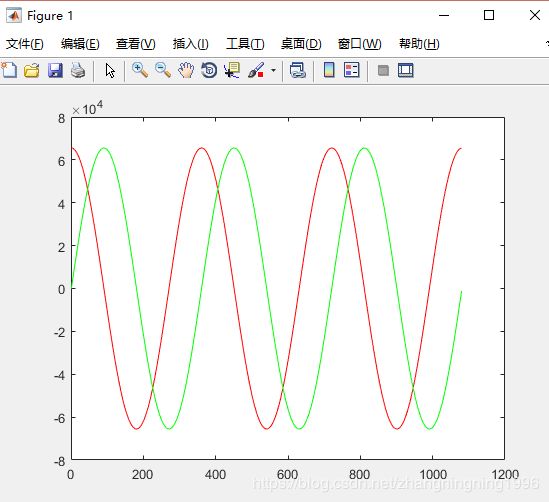
从上面结果可以看出我们实验的正确性。我们利用了CORDIC算法通过计算累加的相位完成了正余弦波形的计算。
FPGA代码
我们将完全按照FPGA代码的书写进行Verilog代码的编写,并且在Modelsim中进行仿真验证。
Cordic_Test模块:
`timescale 1ns / 1ps
// *********************************************************************************
// Project Name : OSXXXX
// Author : zhangningning
// Email : [email protected]
// Website : https://blog.csdn.net/zhangningning1996
// Module Name : Cordic_Test.v
// Create Time : 2020-06-15 16:06:58
// Editor : sublime text3, tab size (4)
// CopyRight(c) : All Rights Reserved
//
// *********************************************************************************
// Modification History:
// Date By Version Change Description
// -----------------------------------------------------------------------
// XXXX zhangningning 1.0 Original
//
// *********************************************************************************
module Cordic_Test(
input sclk ,
input rst_n ,
input [31:0] phase ,
input phase_en ,
output reg [31:0] cose ,
output reg [31:0] sine ,
output wire data_en
);
//========================================================================================\
//**************Define Parameter and Internal Signals**********************************
//========================================================================================/
parameter PIPELINE = 16-1;
parameter K = 39796;
reg signed [31:0] rot[15:0] ;
reg signed [31:0] x[16:0] ;
reg signed [31:0] y[16:0] ;
reg signed [31:0] z[16:0] ;
reg [17:0] phase_en_delay ;
reg [ 1:0] quad[17:0] ;
//========================================================================================\
//************** Main Code **********************************
//========================================================================================/
initial begin
rot[0] <= 32'd2949120;
rot[1] <= 32'd1740992;
rot[2] <= 32'd919872;
rot[3] <= 32'd466944;
rot[4] <= 32'd234368;
rot[5] <= 32'd117312;
rot[6] <= 32'd58688;
rot[7] <= 32'd29312;
rot[8] <= 32'd14656;
rot[9] <= 32'd7360;
rot[10] <= 32'd3648;
rot[11] <= 32'd1856;
rot[12] <= 32'd896;
rot[13] <= 32'd448;
rot[14] <= 32'd256;
rot[15] <= 32'd128;
end
assign data_en = phase_en_delay[16];
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
z[0] <= 32'd0;
else if(phase <= 90 && phase_en == 1'b1)
z[0] <= phase << 16;
else if(phase > 90 && phase <= 180 && phase_en == 1'b1)
z[0] <= (phase - 90) << 16;
else if(phase > 180 && phase <= 270 && phase_en == 1'b1)
z[0] <= (phase - 180) << 16;
else if(phase_en == 1'b1)
z[0] <= (phase - 270) << 16;
else
z[0] <= z[0];
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
quad[0] <= 2'b00;
else if(phase <= 90 && phase_en == 1'b1)
quad[0] <= 2'b00;
else if(phase > 90 && phase <= 180 && phase_en == 1'b1)
quad[0] <= 2'b01;
else if(phase > 180 && phase <= 270 && phase_en == 1'b1)
quad[0] <= 2'b10;
else if(phase_en == 1'b1)
quad[0] <= 2'b11;
else
quad[0] <= quad[0];
genvar i;
generate
for (i=0; i < 17; i=i+1)
always @(posedge sclk or negedge rst_n)
quad[i+1] <= quad[i];
endgenerate
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)begin
x[0] <= K;
y[0] <= 0;
end else if(phase_en == 1'b1)begin
x[0] <= K;
y[0] <= 0;
end else begin
x[0] <= x[0];
y[0] <= y[0];
end
generate
for (i=0; i < 16; i=i+1)
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0) begin
x[i+1] <= 32'd0;
y[i+1] <= 32'd0;
z[i+1] <= 32'd0;
end else if(z[i] > 0)begin
x[i+1] <= x[i] - (y[i] >>> i);
y[i+1] <= y[i] + (x[i] >>> i);
z[i+1] <= z[i] - rot[i];
end else begin
x[i+1] <= x[i] + (y[i] >>> i);
y[i+1] <= y[i] - (x[i] >>> i);
z[i+1] <= z[i] + rot[i];
end
endgenerate
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0) begin
cose <= 32'd0;
sine <= 32'd0;
end else if(quad[16] == 2'b00) begin
cose <= x[16];
sine <= y[16];
end else if(quad[16] == 2'b01)begin
cose <= -y[16];
sine <= x[16];
end else if(quad[16] == 2'b10)begin
cose <= -x[16];
sine <= -y[16];
end else if(quad[16] == 2'b11) begin
cose <= y[16];
sine <= -x[16];
end else begin
cose <= cose;
sine <= sine;
end
always @(posedge sclk)
phase_en_delay <= {phase_en_delay[16:0],phase_en};
endmodule
测试模块的代码,
Cordic_Test_tb:
`timescale 1 ps/ 1 ps
module Cordic_Test_tb;
// Inputs
reg CLK_50M;
reg RST_N;
reg [15:0] cnt;
reg [15:0] cnt_n;
reg [31:0] Phase;
reg [31:0] Phase_n;
wire [31:0] Sin;
wire [31:0] Cos;
wire [31:0] Error;
wire data_en;
Cordic_Test Cordic_Test_inst(
.sclk (CLK_50M ),
.rst_n (RST_N ),
.phase (Phase ),
.phase_en (RST_N ),
.cose (Cos ),
.sine (Sin ),
.data_en (data_en )
);
initial
begin
#0 CLK_50M = 1'b0;
#10000 RST_N = 1'b0;
#10000 RST_N = 1'b1;
#1000000000 $stop;
end
always #10000
begin
CLK_50M = ~CLK_50M;
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
cnt <= 1'b0;
else
cnt <= cnt_n;
end
always @ (*)
begin
if(cnt == 16'd359)
cnt_n = 1'b0;
else
cnt_n = cnt + 1'b1;
end
//生成相位0-359度,Phase[17:16]为相位的象限,Phase[15:10]为相位的值
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
Phase <= 1'b0;
else
Phase <= cnt;
end
endmodule
仿真结果如下:

从上面MATLAB与Modelsim的联合仿真验证,从而证明了我们实验的正确性。
小结
至此为止,我们利用两篇文章介绍了圆周系统的向量模式与旋转模式,至于线性系统与双曲线系统的两种模式在这就不做过多的介绍,相信大家从这两篇文章再结合参考文献中的文章可以很轻松的写出来这两种系统的坐标旋转算法。
大家有没有发现使用CORDIC产生正弦波比DDS要简单的多。
总结
创作不易,认为文章有帮助的同学们可以关注、点赞、转发支持。为行业贡献及其微小的一部分。或者对文章有什么看法或者需要更近一步交流的同学,可以加入下面的群:
![]()