Q learning--强化学习系列文章3
Q learning
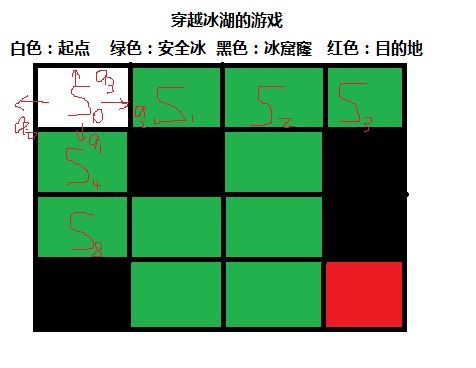
强化学习例子----穿越冰湖的游戏
FrozenLake environment是OpenAI公司(特斯拉公司的老板的另外一个公司,主要研究AI技术)开发的一个环境,这个环境可以让开发者用来练习和测试各种强化学习算法。
代码:
env = gym.make('FrozenLake-v0')
冰封的湖面有4X4个小格子组成,这些小格子有一个是穿越游戏的起点,有些是安全结实的冰面,有些是危险的会陷下去的冰面,有一个是穿越湖面的终点。游戏者每走一步,将会获得一个奖赏值0,除非游戏者成功到达终点,将会获得一个奖赏值1。另外,这个游戏的另一个随机因素是强风,环境中会随机挂起强风,把游戏者刮到随机的位置。这样其实没有确定的一定成功的游戏策略,但整个环境的还是相当稳定,能够训练出能够稳定躲避危险,并到达目的地的游戏策略。
所以我们的目标是开发、训练一个模型,这个模型能够成功的完成这个游戏。
如何把强化学习过程数学表示?---马尔科夫决策过程(MDP)
如何用数学形式表示深度学习问题:MDP(马尔科夫决策过程,Markov Decision Process)。
一个状态与行动对(State, Action),代表在状态State的情况下,执行了动作Action。其后后续将导致两个结果,一个是得到一个立即收益Reward,另外一个结果就是从从一个State转换到另一个State。这种状态转移的过程就构成了MDP。这个过程(例如一局游戏)中只包含了有限的State,Action和Reward的集合。
s
0
,a
0
,--->r
1
,s
1
,a
1
,--->r
2
,s
2
,…,s
n−1
,a
n−1
,--->r
n
,s
n
这里
s
i
代表State,
a
i
是Action,
r
i+1
是执行Action之后的Reward。这段序列结束于最终状态
s
n
(例如游戏结束屏幕)。马尔科夫决策过程依赖于马尔科夫假设,即下一个State
s
i+1
只依赖于当前State
s
i
,与之前的State和Action无关。
Q值表--q-learning的决策依据
现在假设我们拥有这样一张表,(怎样得来的这个表我们将后续学习),每到达一个状态Si,通过查询这张表,我们就立即可以知道最佳的行动a应该是什么。这个表的名称就叫做Q-table。
通过查看openAI公司的环境的源码,我们发现输出0=>左移,1=>下移,2=>右移,3=>上移。如果移动遇到边界,则保持原地。
注意,强化学习的算法并不需要搞清楚输出{0,1,2,3}的移动意义,这里是为了讲课方便同学们理解Q表的意义才去了解这个的。
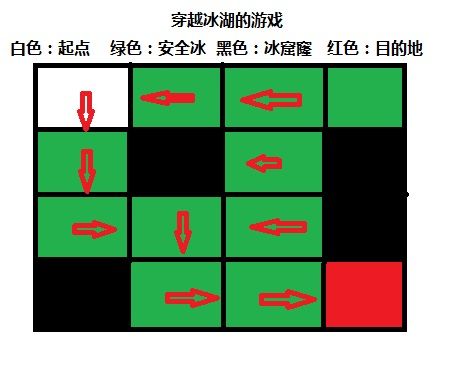
通过查表,我们可以看到穿越路径。
a0 => 左移
a1 => 下移
a2 => 右移
a3 => 上移
S0 [[ 5.65665336e-01 1.32702822e-02 1.84476143e-04 2.78297656e-02]
S1 [ 1.11953138e-03 1.33937995e-04 0.00000000e+00 5.89997642e-01]
S2 [ 2.73597828e-02 0.00000000e+00 5.28510052e-03 5.24379779e-01]
S3 [ 0.00000000e+00 0.00000000e+00 0.00000000e+00 4.26526621e-01]
S4 [ 6.53693362e-01 1.68814092e-03 2.63829516e-03 1.91123462e-03]
S5 [ 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
S6 [ 8.09674056e-02 4.48724195e-05 2.20163475e-09 2.58590894e-06]
S7 [ 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
S8 [ 0.00000000e+00 0.00000000e+00 3.07917957e-03 5.60094060e-01]
S9 [ 3.31391432e-04 4.99781611e-01 0.00000000e+00 0.00000000e+00]
S10 [ 8.47572076e-01 3.13583798e-04 8.98214216e-04 2.51734273e-04]
S11 [ 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
S12 [ 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
S13 [ 1.32122644e-05 5.31944387e-05 8.97199769e-01 4.44037973e-04]
S14 [ 0.00000000e+00 0.00000000e+00 9.96736292e-01 0.00000000e+00]
S15 [ 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]]
通过对Q值表的研究我们发现,通过2千次游戏训练的Q值表并非最优的(和我们站在上帝视角来看这个问题,并非最优路径),但基本可以完成游戏。可能的原因有:游戏中的随机因素的影响;训练的次数不够多,没有收敛到最优的值。
通过上面的讲解,相信同学们对Q值表的意义都有了很好的理解了。下面我们来研究究竟应该怎么来计算Q值表。
如何把未来的收益折现?
为了能有好的长期结果,我们需要考虑的不仅仅是当前的Reward,并且还有将会得到的Reward。但是如何做到呢?
在一个马尔科夫过程中,我们可以很容易的计算一段序列的全部Reward:
R=r
1
+r
2
+r
3
+…+r
n
同理,
t
之后所以的Reward,可以表示为:
R
t
=r
t
+r
t+1
+r
t+2
+…+r
n
但是因为环境是随机的,我们永远也没有办法保证,即使我们执行了相同的Action序列,我们还可以得到相同的Reward。序列进行的越远,分歧可能会越大。因此,通常都会使用折扣的未来奖励:
这里
γ
是折扣系数gama,取值在0和1之间:越远的Reward,我们越少考虑。容易看出,
t
之后的折扣的未来奖励,可以用
t
+1
表示:
R
t
=r
t
+
γ
(r
t+1
+
γ
(r
t+2
+…))=r
t
+
γ
R
t+1
如果设置
γ
=0
,那么我们的策略是短视的,只依赖于当前的Reward。如果想平衡当前和将来Reward,一般设置
γ
=0.9~0.99
。如果我们的环境是确定的,同样的Action序列总是得到相同的Reward,那么可以设置
γ
=1
。
一个好的策略,是总去选择折扣的未来奖励最大的Action。
贝尔曼方程---把现在和未来的收益统一起来
Q(s,a) = r + γ(max(Q(s’,a’))
Q(s,a)表示在观察到状态s后,执行动作a,所对应的Q值。Q值反应的是这对(状态,动作)所处状况的好坏程度。Q值越高,表明处于状态s下执行a动作收益约大。这个收益包括立即得到的收益和未来的收益。
r表示执行动作a之后得到的直接奖励
γ为未来收益折现到现在状态的折现率
在执行完动作之后,环境的新状态为s',为了让该状态的Q值最大化,执行动作a’。
这个公司的所表达的意思很明确:公式定义在状态s下执行动作a对应的Q值Q(s,a)等于接下来的直接收益和下一个状态的最大Q值的折现之和。
Bellman Equation是整个Reinforcement Learning的理论核心。用通俗的话讲就是:如果你要做出一个选择,你需要考虑两个方面,一是你做出选择后立即得到的回报是多少,二是你的选择导致的一系列变化在未来能给你多少回报。将这两者加起来,就是你某项选择的价值。
某个状态下某个动作的Q-value = 该动作导致的直接奖励 + 该动作导致的状态中最有价值动作的Q-value
最后,我们通过一定的学习速率,更新Q值。学习速率一般小于1,这样保证Q值既能根据新信息不断更新,同时又保持相对稳定。
Q值=Q值+学习速率*(新Q值-Q值)
代码:
#不断的更新Q表值
Q[s,a] = Q[s,a] + lr*(r + y*np.max(Q[s1,:]) - Q[s,a])
3.5 解决探索与利用困境
首先,Q-table或者Q-network是随机初始化的,随后初始的预测也是随机的。如果我们选择了最高的Q-value,那么这个选择也是随机的,相当于Agent在进行探索。当Q-function收敛的时候,它会返回稳定的Q-value,探索随之减少。所以我们可以认为,探索是Q-learning算法的一部分。但是这个探索是贪婪的,只要寻找到一个可行的策略之后就好收敛,从而停止探索。
ε-greedy exploration可以简单有效的修正这个问题。ε是随机选择一个Action的概率,否则用贪婪的办法选择Q-value最高的Action。即按照一定概率,选择随机的Action。
#不断的更新Q表值
Q[s,a] = Q[s,a] + lr*(r + y*np.max(Q[s1,:]) - Q[s,a])
算法流程总结
参考:https://github.com/awjuliani/DeepRL-Agents/blob/master/Q-Table.ipynb