CNN 卷积神经网络--kernel、偏置值导数
卷积层
偏置值导数
one thing keep in mind: blj 是一个标量,又因为
zlj=∑i∈MjXl−1i∗klij+blj(2)
而 zlj 每一个元素都是与标量 blj 相关.
因此
根据http://blog.csdn.net/zhongkeli/article/details/51849619,知
δlj=∂E∂zlj(4)
且 δlj 是一个矩阵,因此
∂E∂zluv 等于 (δlj)uv 。
这一部分不知道对不对,但是在求解偏置值导数可以用到http://blog.csdn.net/zhongkeli/article/details/51858297 里面的思想,bias blj 与 zlj 每一个元素都相关,因此 blj 的残差是 zlj 对应的残差与权重(1)加权和.
因此 ∂E∂blj=∑uv(δlj)uv(5)
kernel导数
先给出公式:
∂E∂kernellij=rot180(conv2(xl−1i,rot180(δlj),valid))(6)
这里的kernel对应http://blog.csdn.net/zhongkeli/article/details/51858297的公式(14)中的权重W,但是有一点区别,公式(14)的 wlkj 是一个标量,而这里的 kernellij 是一个矩阵,可以单独求解 kernellij 每一个元素的导数。求解神经网络参数的导数,主要找出与待求解参数相关的神经元的残差(导数)和相应的权重即可求出待求解参数的导数。
推导公式实在很难写,使用图表说明一下求导的过程。
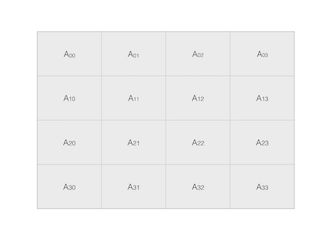
设前一层的输出feature map 为矩阵A
卷积核为K

当前层经过A与K卷积后为矩阵B

矩阵B对应的delta矩阵为D

这一步是求解卷积核K的导数,主要看卷积核K与delta D的关系,因delta D是与为矩阵B一一对应,所以主要关注卷积核K如何生成矩阵B。
B00=A00∗K00+A01∗K01+A10∗K10+A11∗K11(7)
B01=A01∗K00+A02∗K01+A11∗K10+A12∗K11(8)
B02=A02∗K00+A03∗K01+A12∗K10+A13∗K11(9)
B10=A10∗K00+A11∗K01+A20∗K10+A21∗K11(10)
B11=A11∗K00+A12∗K01+A21∗K10+A22∗K11(11)
B12=A12∗K00+A13∗K01+A22∗K10+A23∗K11(12)
B20=A20∗K00+A21∗K01+A30∗K10+A31∗K11(13)
B21=A21∗K00+A22∗K01+A31∗K10+A32∗K11(14)
B22=A22∗K00+A23∗K01+A32∗K10+A33∗K11(15)
跟http://blog.csdn.net/zhongkeli/article/details/51858297的公式(14)可以得出,K的某个元素的导数等于残差D乘以矩阵A相应的值,
比如, K00 与 A00 , A01 , A02 , A10 , A11 , A12 , A20 , A21 , A22 做乘积分别生成 B00 , B01 , B02 , B10 , B11 , B12 , B20 , B21 , B22
因此 K00 的导数为 A00 D00 + A01 D01 +
A02 D02 + A10 D10 + A11 D11 + A12 D12 + A20 * D20 +
A21 D21 + A22 D22
同理可得
K01 与 A01 , A02 , A03 , A11 , A12 , A13 , A21 , A22 , A23 做乘积分别生成 B00 , B01 , B02 , B10 , B11 , B12 , B20 , B21 , B22
则
K00=A00∗D00+A01∗D01+A02∗D02+A10∗D10+A11∗D11+A12∗D12+A20∗D20+A21∗D21+A22∗D22
K‘01=A01∗D00+A02∗D01+A03∗D02+A11∗D10+A12∗D11+A13∗D12+A21∗D20+A22∗D21+A23∗D22
K‘10=A10∗D00+A11∗D01+A12∗D02+A20∗D10+A21∗D11+A22∗D12+A30∗D20+A31∗D21+A32∗D22
K‘11=A11∗D00+A12∗D01+A13∗D02+A21∗D10+A22∗D11+A23∗D12+A31∗D20+A32∗D21+A33∗D22
也就是说
子采样层
对于子采样层的kernel与bias导数,推导过程跟卷积层的推导过程是一样的,只要搞清楚,当前层所求元素对下一层的哪些神经元有贡献,把下一层相关的神经元的残差乘以相应的权重求和即可
参考文献
CNN公式推导
Notes onConvolutional Neural Networks