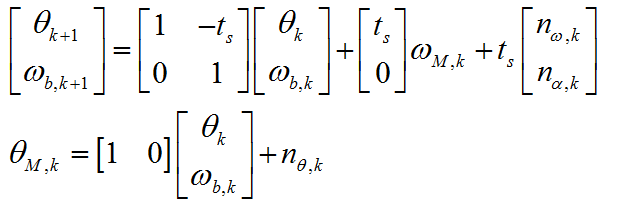对比直立车模控制中的互补滤波、Karlman滤波和参考滤波方案

前几天，有参加智能车竞赛的同学在公众号上询问一个关于直立车模控制中角度融合算法的问题。感觉这是所有初次准备智能车模竞赛的同学都会碰到的问题。

卓大大，请问您可以针对卡尔曼滤波、互补滤波、清华滤波的原理与异同做一个推送吗？最近在查阅相关的资料学习滤波算法，感觉好难理解呀/::<

^{▲ 平衡双轮自行车}

 

01惯性传感器

---

在车模直立控制中被广泛使用的惯性传感器通常是由加速度计和陀螺仪组成。价格比较便宜的惯性测量传感器，输出的信号往往包含有各种噪声。陀螺仪输出车模倾角$\theta$的变化率（角速度）$\dot{\theta }$信号。它通常包括缓慢变化的偏移量${\omega }_b$和高斯白噪声$n_{\omega }$。$$\dot{\theta }={\omega }_T-{\omega }_b-n_{\omega }$$
其中偏移量${\omega }_b$的导数是随机的，通常描述为一个白噪声信号：${\dot{\omega }}_b=n_{\alpha }$。

在重力场中，加速度传感器正交的两个输出，通过求反正切可以传感器相对于重力加速度的倾角。但传感器的运动所产生的加速度也会叠加在输出信号中，进而产生干扰信号。$${\theta }_M={\theta }_T+n_{\theta }$$

^{▲ 采集数据及其显示}

通过滤波器算法将陀螺仪和加速度计所得到的角度信息进行融合，最大限度抑制噪声对测量角度的影响。

前面提问中所提到的三种滤波算法，分别利用传感器噪声不同特点来抑制噪声的影响。看似这些方法原理相差很大，借助于以下条件，能够便于我们进行分析和比较：

• 这三种算法都属于线性滤波算法；
• 在稳态下，可以借助于输入输出之间的传递函数来比较算法的特性；
• 针对车模直立控制，所涉及到的角度只有一个；

 

02三种滤波算法

---

1.参考滤波方案

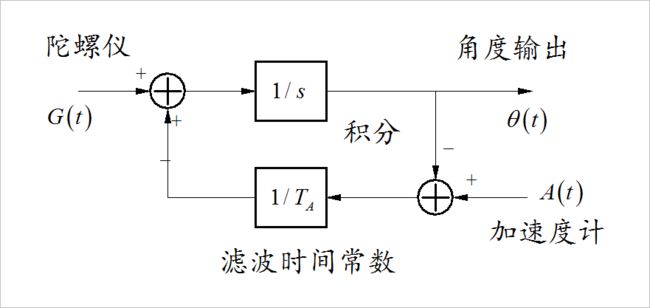
在2012年直立车模组别首次引入智能车竞赛的，竞赛秘书处给出了一个 参考设计方案 。它是在对陀螺仪信号进行积分的基础上，使用加速度计得到的角度信号对输出进行负反馈调节，从而抑制积分中存在的发散问题。下图是参考设计方案中相应的原理框图和程序实现。

^{▲ 参考滤波方案软件实现}

加速度传感器的Z周输出电压$V_a\left(t\right)$（VOLTAGE_GRAVITY），经过偏移量$B_a$（GRAVITY_OFFSET），比率$R_a$（GRAVITY_ANGLE_RATIO）调整之后，形成算法的输入$A\left(t\right)$（g_fGravityAngle）:$$A\left(t\right)=R_a\cdot \left[V_a\left(t\right)-B_a\right]$$

陀螺仪的输出电压$V_g\left(t\right)$（VOLTAGE_GYRO）经过偏移量$B_g$（GYROSCOP_OFFSET），比率$R_g$（GYROSCOPE_ANGLE_RATIO）调整之后，形成算法输入$G\left(t\right)$（g_fGyroscopeAngleSpeed）:$$G\left(t\right)=R_g\cdot \left[V_g\left(t\right)-B_g\right]$$

算法的输出为角度：$\theta \left(t\right)$（g_fCarAngle）。

^{▲ 参考滤波方案的核心算法}

根据参考程序代码，算法可以使用迭代方程描述为：
$$\begin{array}{r}\theta \left[n\right]=T_s\cdot \left\{G\left[n\right]+\frac{1}{T_g}\left\{A\left[n\right]-\theta \left[n-1\right]\right\}\right\}+\theta \left[n-1\right]\\ =T_s\cdot G\left[n\right]+\frac{T_s}{T_g}A\left[n\right]+\left(1-\frac{T_s}{T_g}\right)\theta \left[n-1\right]\end{array}$$

输出角度$\theta \left[n\right]$由两部分线性叠加而成，使用z变换对上面差分方程进行变化，可得：$$\Theta \left(z\right)=H_G\left(z\right)\cdot G\left(z\right)+H_A\cdot A\left(z\right)$$
其中：
$$H_G\left(z\right)=\frac{T_s}{1-\left(1-\frac{T_s}{T_g}\right)z^{-1}},H_A\left(z\right)=\frac{T_s}{T_g}\cdot \frac{1}{1-\left(1-\frac{T_s}{T_g}\right)z^{-1}}$$

通过上面的化简公式可以看出，实际上角度输出信号是陀螺仪和加速度计信号经过一级低通滤波后叠加在一起，所以陀螺仪和加速度计输出信号中如果存在直流分量的漂移，都会引起输出角度信号的零点漂移。

 

2. 互补滤波器

互补滤波器的基本结构如下图所示。假设两个测量信号$B\left(s\right),A\left(s\right)$都包含了实际信号$\theta \left(s\right)$以及噪声。在信号$A\left(s\right)$中的噪声主要分布在高频，而在信号$B\left(s\right)$中的噪声主要分布在低频。

$H\left(s\right)$代表着低通滤波器，那么对应的$1-H\left(s\right)$就是互补的高通滤波器。它们分别提取$A\left(s\right),B\left(s\right)$中的低频和高频成分，然后叠加在一起。

^{▲ 左：基本互补滤波器的结构。右：基本结构的变形，只对噪声进行低通滤波}

在上图右边给出了互补滤波器基本结构的恒等变形。将$B\left(s\right)$与$A\left(s\right)$相减之后，就剩下了高频噪声$n_2$与低频噪声$n_2$相减。再经过低通滤波器$H\left(s\right)$，就剩下$n_1$去抵消$B\left(s\right)$中的低频噪声了。

只所以讨论这个变形，就是因为前面参考方案就是变形的互补滤波器。将陀螺仪信号$G\left(t\right)$的积分看做带有低频噪声（积分漂移信号）的观察信号$B\left(t\right)$。它与加速度计信号$A\left(t\right)$（带有高频运动噪声）相减，后面有比例、积分组成的负反馈组成一个一阶低通滤波器$H\left(s\right)=\frac{1}{T_A\cdot s+1}$，滤波之后与$B\left(t\right)$叠加，形成最后的输出信号。

^{▲ 参考滤波方案本质上是变形后的互补滤波器}

通过上面讨论可以看出，如果在互补滤波器中的低通滤波器的阶次为一阶的话，那么就和前面的参考方案是一致了。在实际应用中，可以增加滤波器的阶次，来提高角度计算的精度。比如在陀螺仪输入信号中，再增加一级高通滤波，可以进一步抑制陀螺仪信号中的直流分量的漂移。

 

3. 卡尔曼滤波

使用卡尔曼滤波的方法来融合来自陀螺仪和加速度计的信号，不在频率范围内考虑它们各自噪声的特点，而是将这两个信号从功能上分为两类。陀螺仪信号${\omega }_M$是过程驱动变量，它激动系统状态（车模倾角，角速度）发生变化；加速度计得到的角度${\theta }_M$则是观察变量，是来修正系统状态。。

选择车模倾角${\theta }_k$和陀螺仪偏变化量${\omega }_b$作为系统状态变量，得到离散系统状态方程为：

令：$$A=\left[\begin{array}{c}\begin{array}{cc}1& -t_s\\ 0& 1\end{array}\end{array}\right],B=\left[\begin{array}{c}\begin{array}{c}{t}_s\\ 0\end{array}\end{array}\right],H=\left[\begin{array}{c}\begin{array}{cc}1& 0\end{array}\end{array}\right],Q=t_s^2\left[\begin{array}{c}\begin{array}{cc}{\sigma }_{\omega }^2& {\sigma }_{\omega \alpha }\\ {\sigma }_{\alpha \omega }& {\sigma }_{\alpha }^2\end{array}\end{array}\right],R={\sigma }_{\theta }^2$$

则对应卡尔曼滤波方程为：

$$\begin{array}{r}{\hat{x}}_{k+1}^{\ast }=A{x}_k+Bu\cdot {\omega }_{M,k}\\ P_{k+1}^{\ast }=A{P}_k{A}^T+Q\\ K_k=P_k^{\ast }{H}^T{\left(H{P}_k^{\ast }{H}^T+R\right)}^{-1}\\ {\hat{x}}_k={\hat{x}}_k^{\ast }+K\left({\theta }_{M,k}-H{\hat{x}}_k^{\ast }\right)\\ P_k=\left(I-K_{k}H\right)P_k^{\ast }\end{array}$$

在这个过程中，如果系统噪声协方差矩阵$Q$以及观测噪声方差$R$始终为常量。那么由上面方程2、3、5迭代之后，误差协方差矩阵$P$和卡尔曼增益矩阵$K$就会逐步收敛到一个常量。

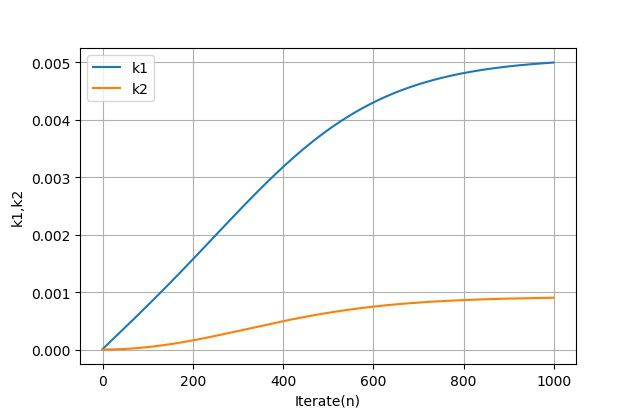
在下面参数下，经过迭代1000次之后，卡尔曼增益矩阵参数$K={\left(k_1,k_2\right)}^T$的变化曲线。可以看去它逐渐曲线与常数${\left(0.005,0.001\right)}^T$。
$$t_s=0.01,{\sigma }_{\omega }^2=1.505\times 10^{-3},{\sigma }_{\alpha }^2=1.721\times 10^{-4},{\sigma }_{\omega ,\alpha }^{}=0,R=250$$

^{▲ K参数迭代数值}

当$K$为常量的时候，对方程1、4再联立起来，就形成关于状态变量${\hat{x}}_k={\left({\theta }_k,{\omega }_{b,k}\right)}^T$的差分方程。考虑到$k_1,k_2$，$t_s$都比较小，将化简过程中涉及到这些小量乘积（二阶小量）都省略掉，那么最终可以将输出角度$\theta$与输入${\omega }_M,{\theta }_m$之间的差分方程化简为：$$\Theta \left(z\right)=\frac{t_s}{1-\left(1-k_1\right)z^{-1}}G\left(z\right)+\frac{k}{1-\left(1-k_1\right)z^{-1}}A\left(z\right)$$

其中$\Theta \left(z\right),G\left(z\right),A\left(z\right)$分别是$\theta \left[n\right],{\omega }_M\left[n\right],{\theta }_M\left[n\right]$的z变换。对照上面简化的输入输出之间的关系与前面参考方案中对应的方程，可以看到卡尔曼滤波器本质上和互补滤波器是相同的。如果不省略那些参数小的项数，滤波算法就变成二阶的互补滤波器的形式了。

观察噪声$R$来自于加速度计传感器，系统内部噪声$Q$来自于陀螺仪。当$R$远远大于$Q$的时候，所计算出的卡尔曼滤波增益$K$的数值比较小，这样才能够进行上述的算法简化。

 

03算法关系

---

可以看出。当所使用的惯性传感器，陀螺仪的噪声远远低于加速度传感器的噪声时，低通滤波器的阶次取一阶滤波器的情况下，三种滤波器的算法效果在平稳状态下是相同的。

从原理上，参考方案与互补滤波器比较接近，它们是利用不同传感器噪声在频率上的差别抑制噪声的。卡尔曼滤波器则根据传感器对倾角影响的机制不同，通过构造系统状态变量将信息进行融合。

在车模直立控制应用中，互补滤波器和参考方案所需要的计算量小，参数只有滤波时间常数$T_A$，调试相对比较简单。但该算法对于陀螺仪工作点的漂移无法抑制，使用时，可以对陀螺仪信号再通过一个高通滤波器，消除陀螺仪信号工作点变化对输出角度的影响。

卡尔曼滤波器计算量相对较大，适应于高速控制器。由于卡尔曼滤波器内部变量包括有对陀螺仪工作点的估计，所以陀螺仪的工作点的缓慢变化不会影响计算角度的变化。

^{▲ RECORD1数据}

在使用滤波器算法的时候，都会涉及到算法的初始状态的设置问题。对于互补滤波器相对比较简单，将内部积分累加变量初始化为0便可以适应大部分情况。对于卡尔曼滤波器，它的参数矩阵$P$则需要选择恰当的初始值，以使得算法尽快达到收敛的目的。比如可以将算法收敛后的$P$矩阵的值作为程序下一次运行的初始值，这样就可以更快使得算法进入稳定状态。

此外，需要根据传感器输出信号的实际情况，合理的确定卡尔曼滤波器中的$Q,R$参数，这样才能够在算法的收敛以及滤波效果方面取得良好的平衡。

关于这三种算法在理论上的分析就到这里，它们在实际控制中的效果以后在给出。