图的遍历（搜索）算法 之 深度优先遍历算法

图的遍历的定义：              

       从图中的某个顶点出发访问遍图中的所有顶点，并且每个顶点仅仅被访问一次。

       图的遍历算法我们常见的而且用的最多的就有两种：其一是图的深度优先遍历算法；其二是图的广度优先遍历算法。这里我们先说一下图的深度优先遍历算法。

       ★连通图的深度优先遍历算法（DFS）类似于二叉树的先序遍历。★

深度遍历算法的基本思想：

图的深度遍历算法粗略的可以分为以下三步骤：

   （1）首先选定一个未被访问过的顶点V作为起始顶点（或者访问指定的起始顶点V），并将其标记为已访问过；

   （2）然后搜索与顶点V邻接的所有顶点，判断这些顶点是否被访问过，如果有未被访问过的顶点，则任选一个顶点W进行访问；再选取与顶点W邻接的未被访问过的任一个顶点并进行访问，依次重复进行。当一个顶点的所有的邻接顶点都被访问过时，则依次回退到最近被访问的顶点。若该顶点还有其他邻接顶点未被访问，则从这些未被访问的顶点中取出一个并重复上述过程，直到与起始顶点V相通的所有顶点都被访问过为止。

   （3）若此时图中依然有顶点未被访问，则再选取其中一个顶点作为起始顶点并访问之，转（2）。反之，则遍历结束。

那么问题来了,我们如何判断起始顶点V的邻接顶点是否被访问过呢？

     解决办法：为每个顶点设立一个“访问标志Visited”。首先将图中每个顶点的访问标志设为 “0”或FALSE表示未访问，“1”或true表示已访问,  之后搜索图中每个顶点，如果未被访问，则以该顶点为起始点，进行深度优先遍历，否则继续检查下一顶点。

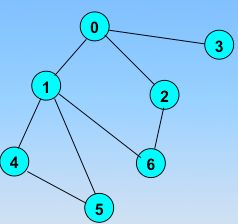
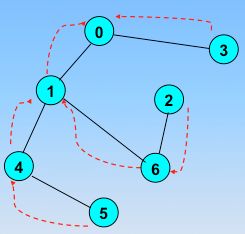
接下来我们用一个例子来说明，图的顶点和弧如下图，假定我们以V0作为起始顶点进行遍历。

☞ 访问指定的起始顶点V0，并将visited[V0]=1然后输出V0顶点；若当前访问的顶点的邻接顶点有未被访问的顶点{V1,V2,V3}，则任选一个访问之；（这里我们选V1顶点）

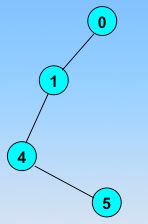
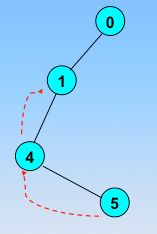
☞ 访问V1顶点，并将visited[V1]=1然后输出V1;然后V1未被访问过的邻接顶点有{V4,V5,V6},则任选一个顶点进行访问；（这里我们选择V4顶点，并将visited[V4]=1然后输出V4）......依次的这样访问下去，直到某个顶点（V5）的邻接的顶点都已经被访问为止。此时应该回退到最近访问过的顶点，直到与起始顶点相通的全部顶点都访问完毕；从顶点V5回退到V4，再回退到V1，发现有新的未被访问的顶点{V6}

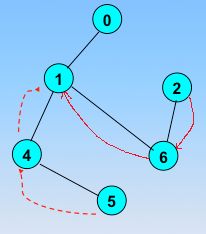
☞此时就要访问V6，并将visited[V6]=1，再输出V6；然后选取V6未被访问的邻接的顶点{V2}进行访问，并将visited[V2]=1然后输出V2；这是V2的邻接顶点都已经被访问，此时再回退到V6，发现V6邻接顶点也都已经被访问，继续回退到V1

☞由于与V1邻接的顶点也都已经被访问，继续回退到V0

☞发现V0还有未被访问的顶点{V3}，然后访问V3，将visited[V3]=1，再输出V3；此时V3的所有邻接的顶点都已经被访问，继续回退到V0

此时，所有的顶点均被访问，结束搜索。

顶点的访问序列为：V0,V1,V4,V5,V6,V2,V3(不唯一)。

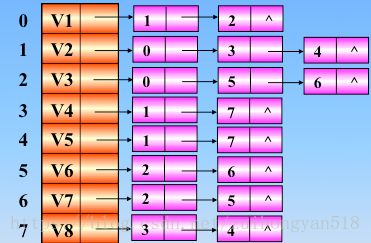
实现过程：依靠栈，一维数组和图的邻接矩阵存储的方式

图的邻接矩阵

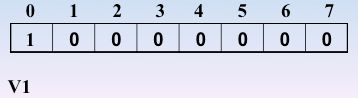
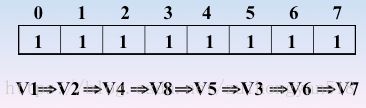
使用一个一维数组存储所有的顶点，对应的下标的元素为1（代表已经被访问），0（代表没有被访问）

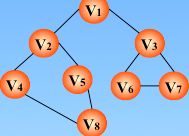
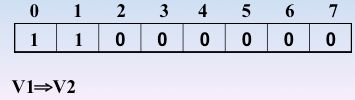
☛先访问 v1，0进栈，0处置为1

☛继续访问 v2，1进栈，1处置为1

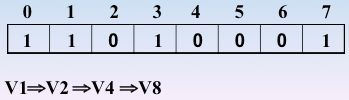
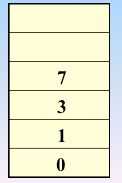
☛继续访问v4（依据邻接矩阵），3入栈，3处置为1

☛继续访问 v8，7入栈，7处置为1

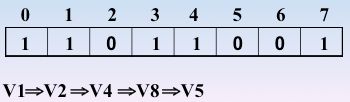
☛继续访问 v5，4入栈，4处置为1

☛继续访问，发现没有还没访问的结点了，那么好，退栈（也就是回退）开始，回退到 v1处，也就是0的时候，发现了没有被访问的结点，那么继续访问之

☛继续访问 v3，2进栈，2处置为1，继续访问v6，5进栈，5处置为1，继续访问v7，6进栈，6处置为1

☛发现没有还没被访问的结点了，那么好，继续回退（也就是退栈的过程）

遍历图的过程实质上是对每个顶点查找其邻接点的过程，所耗费的时间取决于所采用的存储结构。
对图中的每个顶点至多调用1次DFS算法，因为一旦某个顶点已访问过，则不再从它出发进行搜索。

邻接链表表示：查找每个顶点的邻接点所需时间为O(e)，e为边(弧)数，算法时间复杂度为O(n+e)

数组表示：查找每个顶点的邻接点所需时间为O(n2)，n为顶点数，算法时间复杂度为O(n2)

代码如下：                           

int visited[maxSize];     //访问标志的数组

/* V是起点的编号，visited[]是一个全局的数组，作为顶点的访问标记，初始时所有的元素均为0，0表示未被访问过，即所有的元素都没有被访问过。因图中可能存在回路，当前经过的顶点在将来还可能再次经过，所以要对每一个顶点进行标记，以免重复访问。

*/

void DFS(AGraph *G,int V)

{

     ArcNode *p ;    //图的顶点的搜索指针

     visited[v]=1;   //置已经访问

     printf("%d",v);   //输出访问过的顶点

     visited(v);      //函数visited()代表了一类访问顶点v的操作

     p=G->adjlist[v].firstarc;   //p指向顶点v的第一条边

     while(p != null){

           if(visited[p->adjvex]==0)     //若顶点未访问，则递归访问它

                  DFS(G,p->adjvex);

          p = p->nextarc;      //p指向顶点v的下一条边的终点

      }

}