摩拜单车数据初探

项目背景

此项目是2017年biendata上的一个比赛项目，赛事方提供了300万行的训练数据和200万行的测试数据，旨在预测用户骑行目的地的区块位置。
本文将使用项目中给出的训练集数据train.csv进行数据的探索性分析，利用python工具来探索用户骑行规律，暂不涉及建模。

数据概况

现在开始吧！

#常规操作，首先导入各种需要的包
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from math import radians,cos,sin,asin,sqrt
%matplotlib inline

#读取训练集和测试集
train = pd.read_csv('./MOBIKE_CUP_2017/train.csv', sep = ',', parse_dates = ['starttime'])
test = pd.read_csv('./MOBIKE_CUP_2017/test.csv', sep = ',', parse_dates = ['starttime'])

#看看数据长什么样子
train.head()

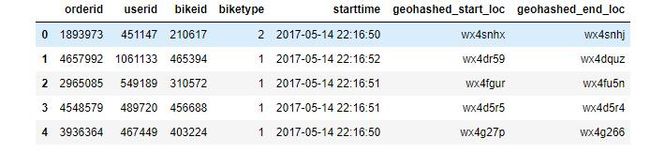
emmmm，geohash是啥？查一下。
Geohash精度和原理，感兴趣的可以查看一下，这里不探究，只应用。

首先安装

!pip install geohash

然后导入

import geohash

然后继续查看数据情况

#测试集的情况
test.head()

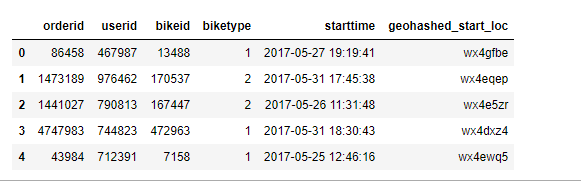
训练集有320万条数据，测试集有200万条数据，训练集比测试集多了一列geohashed_end_loc，即是测试集需要预测的目的地，不过本次不做预测分析。

训练数据涉及近35万用户，48万辆车，2种车型。

数据处理

由于自己电脑配置原因（哭?，大哭??，使劲哭???），数据量较大运行较慢，所以将原测试集数据随机挑选50%进行分析。

train = train.sample(frac=0.5)

进行数据处理

def _processData(df):
    #将starttime 分成weekday,day,hour三类，方便后续不同时间段数据展示
    df['weekday'] = df['starttime'].apply(lambda s : s.weekday())
    df['day'] = df['starttime'].apply(lambda s : str(s)[:10])
    df['hour'] = df['starttime'].apply(lambda s : s.hour)
    print('时间处理完成！！！')
    
    #将geohash字符串反编码，方便后续计算骑行距离
    df['start_lat_lng'] = df['geohashed_start_loc'].apply(lambda s : geohash.decode(s))
    df['end_lat_lng'] = df['geohashed_end_loc'].apply(lambda s : geohash.decode(s))
    df['start_neighbors'] = df["geohashed_start_loc"].apply(lambda s : geohash.neighbors(s))
    
    #原数据中的geohash字符串是g7，现在转成g6
    df['geohashed_start_loc_6'] = df['geohashed_start_loc'].apply(lambda s : s[:6])
    df['geohashed_end_loc_6'] = df['geohashed_end_loc'].apply(lambda s : s[:6])
    df['start_neighbors_6'] = df["geohashed_start_loc_6"].apply(lambda s : geohash.neighbors(s))
    print('Geohash处理完成！！！')
    
    #判断目的地是否在neighbors
    def inGeohash(start_geohash, end_geohash, names):
        names.append(start_geohash)
        if end_geohash in names:
            return 1
        else:
            return 0
    df['inside'] = df.apply(lambda s : inGeohash(s['geohashed_start_loc'],s['geohashed_end_loc'],s['start_neighbors']), axis = 1)
    df['inside_6'] = df.apply(lambda s : inGeohash(s['geohashed_start_loc_6'],s['geohashed_end_loc_6'],s['start_neighbors_6']), axis = 1)
    print("Geohash近邻判断处理完成！！！")
    
    #计算起点与终点距离
    def haversine(lon1, lat1, lon2, lat2): 
        """
        Calculate the great circle distance between two points 
        on the earth (specified in decimal degrees)
        """
        lon1, lat1, lon2, lat2 = map(radians, [lon1, lat1, lon2, lat2])
        # haversine公式
        dlon = lon2 - lon1 
        dlat = lat2 - lat1 
        a = sin(dlat/2)**2 + cos(lat1) * cos(lat2) * sin(dlon/2)**2
        c = 2 * asin(sqrt(a)) 
        r = 6371 # 地球平均半径，单位为公里
        return c * r * 1000
    df['start_end_distance'] = df.apply(lambda s : haversine(s['start_lat_lng'][0],s['start_lat_lng'][1],s['end_lat_lng'][0],
                                                             s['end_lat_lng'][1]),axis = 1)
    print("距离计算完成！！！")
    return df

基本思路：
1.将起始日期分成星期，天，小时，方便后续进行不同时间的分析；
2.将geohash编码进行反编码，进行骑行距离的计算，并用neighbors方法算出以起点为中心的九宫格编码；
3.考虑到geohash7位编码距离较小，仅为153m × 153m的范围，实际骑行中基本都能超出范围，所以将7位编码转化成6位编码，范围增加到 1.22km × 0.61km，较为符合实际情况；
4.利用geohash判断训练集中的目的地是否在九宫格内；
5.计算骑行距离，公式直接从网上找的

上个厕所，倒杯水，等待数据处理完成。emmmmm，好像有什么不对的地方。

处理后的数据

数据分析

时间段上的分析

def _timeAnalysis(df):
    #数据包含的天数
    print('数据集包含的天数如下：')
    print(df['day'].unique())
    print('*'*60)
    
    #用户出行小时高峰期
    g1 = df.groupby('hour')
    print(g1['orderid'].count().sort_values(ascending = False))
    print('*'*60)
    
    #周一到周日用车分析
    g1 = df.groupby('weekday')
    print(pd.DataFrame(g1['weekday'].count()))
    print('*'*60)
    
    #周一到周日不同时间的用车分析
    df.loc[(df['weekday'] == 5) | (df['weekday'] == 6), 'isWeekend'] = 1
    df.loc[~(df['weekday'] == 5) | (df['weekday'] == 6), 'isWeekend'] = 0
    g1 = df.groupby(['isWeekend', 'hour'])
    
    #计算工作日以及周末的天数
    g2 = df.groupby(['day', 'weekday'])
    w = 0 #周末天数
    c = 0 #工作日天数
    for i,j in list(g2.groups.keys()):
        if j >= 5:
            w += 1
        else:
            c += 1
    
    temp_df = pd.DataFrame(g1['orderid'].count()).reset_index()
    temp_df.loc[temp_df['isWeekend'] == 0 , 'orderid'] = temp_df['orderid']/c
    temp_df.loc[temp_df['isWeekend'] == 1 , 'orderid'] = temp_df['orderid']/w
    print(temp_df.sort_values(['isWeekend', 'orderid'], ascending = False))
    sns.barplot(x = 'hour', y = 'orderid', hue = 'isWeekend', data = temp_df)

训练集中的日期总共有14天

早上7点/8点及下午6点/7点骑行订单最多，符合早晚高峰出行的实际情况。

周一到周日订单基本都在20万左右，周三周四最多。

周末订单很少，订单最多的是工作日早晚高峰时期。从下图也可以看出。


从骑行距离的统计来看，大部分人都骑行不超过1公里，较为符合短途骑行的特点。最远的有40公里，属于异常值。
将超过5公里的去掉，查看分布情况。

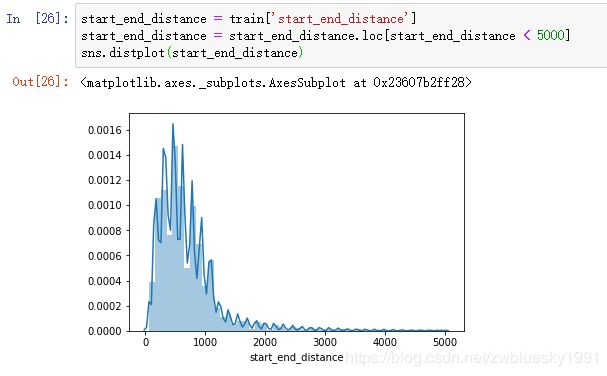
绝大多数骑行距离不超过1公里。


在不同时间上的平均骑行距离基本是一致的，没有特别突出的情况。

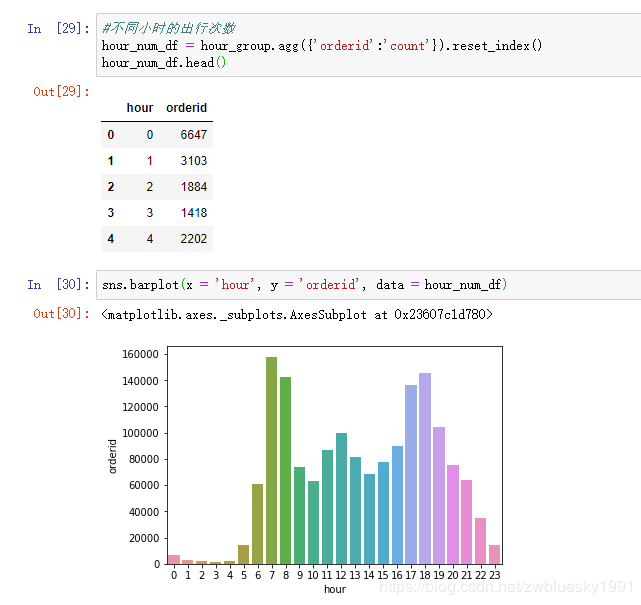
结果依然是早晚高峰出行次数最多。

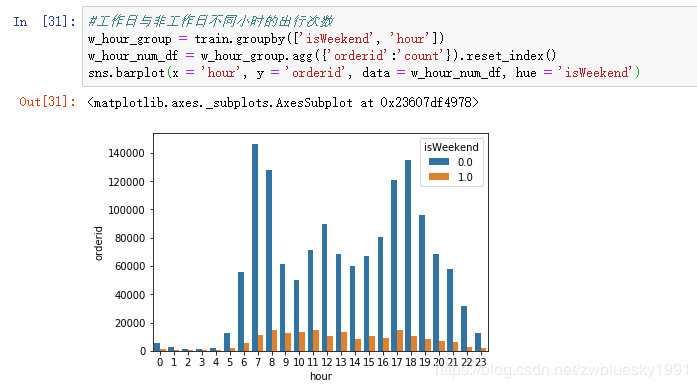
通过对比可以看出双休日没有早晚高峰出行特点。
小结：出行时间与是否工作日这两个特征对用户行为有着重要的影响。

下面分析一下起点和终点。
首先看一下每天从起点出发或到达的订单、用户、车辆。

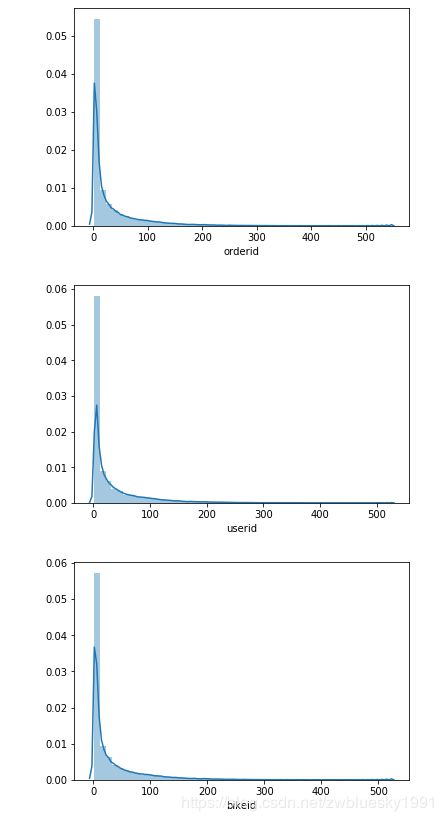
基本每个范围的数量大部分在100以下。
再看一下固定起点终点的订单、用户和车辆。

start_end = train.groupby(["day","geohashed_start_loc","geohashed_end_loc"])
# 计算 出发点-停车点 的 订单量，车辆数，用户数
start_end.agg({"orderid":"count","userid":"nunique","bikeid":"nunique","start_end_distance":"mean"}).reset_index().sort_values(by = "orderid",ascending = False)

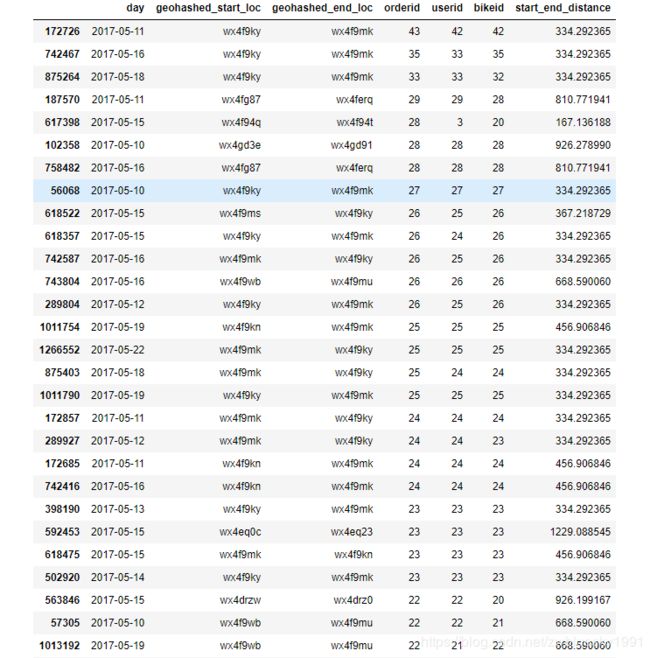
看到最多的也没超过50个。
结合上面每个范围每天的数据，是否可以预测安排每个点的单车数量？这些都有待继续探讨。
本文并未涉及到模型分析，待后面学习深入后，再回头补。
如果本文有错误或者不当之处，欢迎各位大佬留言评论，感谢！