Educational Codeforces Round 49 (Rated for Div. 2)
链接：http://codeforces.com/contest/1027
目录
A.Palindromic Twist
题目
题解
代码
B.Numbers on the Chessboard
题目
题解
代码
C.Minimum Value Rectangle
题目
题解：
代码
D.Mouse Hunt
题目
题解
代码
A.Palindromic Twist
题目
给一个纯小写字母的字符串。字符串的每个字母都必须变化成其字母表中的前一个或后一个，即c变成b或者d，但是a只能变成b，z只能变成y。 要求字符串所有的字符都要变一次，问能否使得最终结果形成一个字符串。
题解
由于必须变化，所以两个字母能回文的要求就是它们相等或者它们字母表众中的距离正好相差2（例如b和d）。
代码
#include
#include
#include
#include
#include
#include
#include B.Numbers on the Chessboard
题目
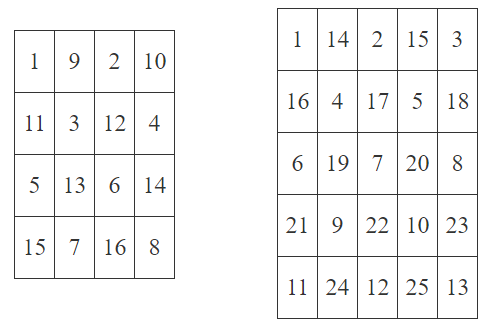
给一个n，有一个n*n的正方形。
按照这样子往格子里面填数字。
给定q组询问，每组询问给出x和y，要求填在(x,y)上的数。
题解
无脑模拟就行了。无穷if else。
代码
#include
#include
#include
#include
#include
#include
#include C.Minimum Value Rectangle
题目
给n个木棍，要求任选4根组成长方形，记长方形周长为C，面积为S，使得
最小。
输出任意一组满足条件的解。
题解：
想法1：如果两根木棍长度分别为a和b，那么如果|a-b|越小，则也越小。原问题转化为求数组元素的最小间距。
后来发现是不对的，反例：1和2，100和102。应该选后者- -
想法2：假设两根木棍长度分别为a和b，那么 = 
，这是约分出来的。由于只要使其尽量小，所以舍去常数项。
式子的最终形式变成 
。
我们比较将数量>=2的木棍排完序后，依次放到上述式子去比较。
一定是两个距离相邻的木棍去比较，比如a和b最近(b>a)，那么b+1（甚至b+d,d>0) 为什么不行呢?
可以作差证明
, +d和+1证明的方法都是一样的。
代码
注意：不用每次都memset e数组，不然会TLE！！！！memset也是耗时间的。
#include
using namespace std;
#define INIT(x) memset(x,0,sizeof(x))
#define eps 1e-8
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 1000005;
inline void read(int &x)
{
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
inline void print(int x)
{
if(x<0){ putchar('-'); x=-x;}
if(x>9) print(x/10);
putchar(x%10+'0');
}
inline double fx(int a, int b)
{
return (a*1.0)/b + (b*1.0)/a;
}
int t,n;
int a[maxn];
int cnt[10005];
bool vis[10005];
int e[maxn/2];
int main()
{
cin>>t;
while(t--) {
INIT(cnt);
INIT(vis);
cin>>n;
int tot = 0;
bool flag = 0;
int ans;
for(int i=0;i=4) {
ans = a[i];
flag = 1;
}
}
if(flag) {
cout<=2&&!vis[a[i]]) {
vis[a[i]] = 1;
e[tot++] = a[i];
}
}
// for(int i=0;i D.Mouse Hunt
题目
老鼠可能在1-n任意一个洞出没。
先给出n个数，表明每个洞安放老鼠价要花费的价格，再给出n个数，其中第i个表示老鼠在i出现后会去a[i]。
要捕捉到老鼠，问要花费的最小价格。
题解
要捕捉到老鼠的条件就是出现自环，这是基本条件。然后DFS即可。
dfs时会出现3种情况：
- 自己到自己，比如a[1] = 1，那么直接和底下的一样；
- 转成一圈回到之前遍历过的点（必须是这次转圈过程中遍历到的）， 那么以那个点开始转圈，挨个统计最小值；
- 已经处理好了一个圈，这时候有个其他顶点连了过来。这种情况结果就是0，因为结果在刚才那个圈里面已经统计过了。
代码
#include
using namespace std;
#define INIT(x) memset(x,0,sizeof(x))
#define eps 1e-8
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 200005;
int c[maxn],a[maxn],pre[maxn],n;
int vis[maxn];
inline void read(int &x)
{
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
inline void print(int x)
{
if(x<0){ putchar('-'); x=-x;}
if(x>9) print(x/10);
putchar(x%10+'0');
}
inline void caltime(int tt) {
tt = clock() - tt;
cerr << (double)tt/CLOCKS_PER_SEC << " seconds!" << endl;
}
int dfs(int x,int q) {
if(vis[x]!=0) {
if(vis[x]!=q) { //如果有其他点的终点也是x，那么就可以不用算了
return 0;
}else {
int temp = x; //这条路是第一次算钱，把终点能到的所有地方全算一遍，必然会形成环，否则无解
int val = c[x];
x = a[x];
while(x!=temp) {
val = min(val,c[x]);
x = a[x];
}
return val;
}
}
vis[x] = q;
dfs(a[x],q);
}
int ans;
int main()
{
cin>>n;
//int tt = clock();
for(int i=1;i<=n;i++)
read(c[i]);
for(int i=1;i<=n;i++) {
read(a[i]);
}
for(int i=1;i<=n;i++) {
if(!vis[i]) {
ans += dfs(i,i);
}
}
cout<