深度强化学习—— 译 Deep Reinforcement Learning(part 0: 目录、简介、背景)

翻译说明

本文译自 Yuxi Li 2018版的长篇综述《Deep Reinforced Leaning》（
arXiv:1810.06339）。有删减 （翻译始于2019/07/20）
文中小括号()内的斜体中文，为译者根据上下文义自行补全的。
本篇仅展示概述部分，各章详细内容见链接。

综述

本文以概述的风格讨论了深度强化学习（Deep RL），结构宏大又不乏细节，侧重于当代工作和历史背景。讨论了DRL的六个核心要素，六个重要机制和十二个应用方向。
本文首先介绍人工智能（Artificial Intelligence，AI）、机器学习（Machine Learning）、深度学习（Deep Learning）和强化学习（Reinforcement Learning，RL）的背景和资源。
然后讨论RL的核心要素，包括价值函数（value function）、策略（policy）、激励（reward)、模型（model），探索与利用（exploration vs. exploitation）和表征（representation）。
然后讨论RL的重要机制，包括注意力（attention）和记忆（memory）、无监督学习（unsupervised learning）、分层RL（hierarchical RL）、多智能体RL(multi-agent RL)、关系RL(relational RL) 和 元学习(learning to learn）。
然后讨论RL的应用，包括游戏、机器人、自然语言处理（NLP）、计算机视觉、金融、商业管理、医疗保健、教育、能源、交通、计算机系统，以及科学、工程和艺术。
最后，我们做了一个简要的总结、并探讨了挑战与机遇、并以一个后记作结。
关键词：deep reinforcement learning, deep RL, algorithm, architecture, application, artificial intelligence, machine learning, deep learning, reinforcement learning, value function, policy, reward, model, exploration vs. exploitation,representation, attention, memory, unsupervised learning, hierarchical RL, multiagent RL, relational RL, learning to learn, games, robotics, computer vision, natural language processing, finance, business management, healthcare, education,energy, transportation, computer systems, science, engineering, art

1 简介

RL是指，与环境相互作用的智能体(agent)通过反复实验（trial and error）为(自然科学、社会科学及工程等广泛领域的）顺序决策问题学习最优策略。（Sutton和Barto， 1998; 2018; Bertsekas和Tsitsiklis，1996; Bertsekas，2012; Szepesv’ari 2010; Powell，2011）。

RL和神经网络的整合历史悠久。省略三段…

创造力将进一步推动Deep RL在核心要素、重要机制和应用方面的开拓发展，似乎没有边界。 任何可以被视为或转变为顺序决策问题的问题，RL都可能会有所帮助。

为什么深度学习能够帮助RL取得如此多的重大成就？深度学习的表征学习(representation learning)可以通过梯度下降实现自动特征工程(feature engineering)和端到端(end-to-end)学习，从而显著的减少甚至消除对某些问题的领域知识的依赖。过去特征工程是手动完成的，这种方法是耗时、over-specified且不完整的。深度分布式表示利用数据中因素的层次结构来对抗维数灾难（curse of dimensionality）的指数挑战。深度神经网络的通用性、富于表现性、灵活性 使得一些任务的表示更加容易或可实现，例如前面讨论的在架构、算法和应用中的突破。

作为一种特定的机器学习类型，深度学习并非没有限制，例如，作为缺乏可解释性（interpretability）的黑盒子，或者说是没有明确和充分的科学原理的“炼金术”，难以调整超参数（hyperparameters）, 没有人类智能，在某些任务中甚至无法与婴儿竞争。Deep RL加剧了这些问题，甚至可重复性(reproducibility)也是一个问题（Henderson et al.,2018）。 然而，我们看到了一个光明的未来，因为有很多工作正在改进深度学习，机器学习，强化学习，深度强化学习和一般的AI。

深度学习和RL分别在2013年和2017年被选为MIT十大突破性技术之一，将在实现人工智能方面发挥关键作用。 AlphaGo的主要贡献者David Silver（Silver et al.，2016a; 2017）提出了一个猜想：人工智能=强化学习+深度学习（Silver，2016）。 我们将在第21章进一步讨论这个猜想。

关于Deep RL有以下几个常见问题。 我们将在下面这些问题进行简要讨论，并在接下来的章节中对其进行进一步阐述。

• Why deep?
• What is the state of the art(最先进的)?
• 问题及可能的解决方案是什么?

本文大纲如下,略…

图1显示了本文的大纲。 智能体 - 环境交互位于中心，外面是核心元素，然后是重要机制，最后是各种应用。

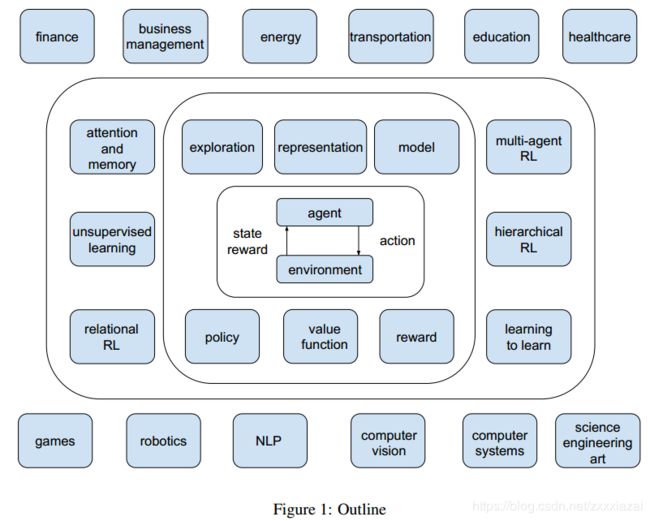
本文面向的读者主要是那些希望深入了解Deep RL的人，尤其是初次接触(deep)RL的新手。 对于强化学习专家以及新人，本书有助于作为参考。 本文有助于学习 Deep RL课程，包括选定的主题和论文。

我们努力讨论最近的具有代表性的工作，并直观的、提纲挈领的、概念性的提供尽可能多的相关信息。我们试图使这个手稿成为Sutton和Barto（Reinforcement Learning：An Introduction (2nd Edition) ,2018）的补充，这本RL的经典著作主要关注RL的基本原理。 然而，深度RL本质上是一个advanced topic; 本手稿的大部分内容都是在介绍论文，大部分内容都没有详细论述。 （否则，稿件长度会爆炸。） 因此，本文的大部分内容都是技术性的，有点粗糙，没有完整的细节。 原始论文通常是深入理解这些内容的最佳资源。
Deep RL正在快速发展。 我们发布博客以补充本手稿，并努力跟踪该领域的发展，网址为 https://medium.com/@yuxili。
本手稿涵盖了深层强化学习的广泛主题。 尽管我们已经尽力追求卓越，但不可避免地存在缺陷甚至是错误。 欢迎提出意见和批评。

2 背景

本章将简要介绍人工智能、机器学习、深度学习和强化学习的概念和基本原理。

我们没有对人工智能、机器学习、深度学习作详细的背景介绍，而是推荐了如下最近的Nature/Science的综述论文：
Jordan, M. I. and Mitchell, T. (2015). Machine learning: Trends, perspectives, and prospects. Science,349(6245):255–260.
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature, 521:436–444.
对于强化学习，我们将介绍一些基础知识作为迷你教程，并推荐
教科书：
Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learning: An Introduction (2nd Edition). MIT Press，
两门课程：
Silver, D. (2015). UCL reinforcement learning course. http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html
Levine, S. (2018). CS 294: Deep reinforcement learning. http://rail.eecs.berkeley.edu/deeprlcourse/.
以及最近的Nature综述文献：
Littman, M. L. (2015). Reinforcement learning improves behaviour from evaluative feedback. Nature,521:445–451）
我们在2.5节中介绍了一些Deep RL的资源。

图2说明了AI和机器学习中几个概念之间的关系。正如其名称所示，深度强化学习处于深度学习和强化学习的交叉点。我们通常将机器学习分类为监督学习，无监督学习和强化学习。深度学习可以与监督学习，无监督学习，强化学习和其他机器学习方法一起使用。深度学习是机器学习的一部分，机器学习是AI的一部分。 请注意，所有这些领域都在不断地发展，例如，深度学习和Deep RL正在解决经典的AI问题，如逻辑，推理和知识表示。 强化学习对于所有AI问题都很重要，正如Russell和Norvig所说，“甚至可以认为强化学习包含了所有的AI：一个智能体被置于一个环境中，必须学会在其中成功地行事”，并且，“强化学习可以被视为整个AI问题的缩影”。

Figure: 2

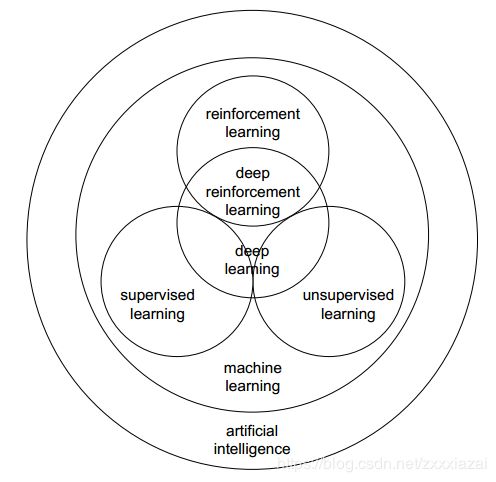
2.1 人工智能

AI是一个非常广泛的领域。 甚至像*Russell, S. and Norvig, P. (2009). Artificial Intelligence: A Modern Approach (3rd edition). Pearson.*这样的权威AI教科书也没有给出精确的定义。Russell和Norvig在两组对比中从四个角度讨论了AI的定义：1）思维过程与推理 vs. 行为；2） 在忠实重现人类表现方面取得成功 vs. 合理性，理想表现的度量标准。我们遵循Russell和Norvig的讨论，列出了四种AI的定义方法。

定义1，“行为人性化”（acting humanly），遵循图灵测试方法。”创造这样一种机器的艺术：机器执行的功能，当人类执行时需要运用智能才能完成 “，“研究如何使计算机做（目前来看）人类做的更好的事”。

如果人类询问者无法判断对某些书面问题的书面答复是来自计算机还是人类，那么计算机就通过了图灵测试。计算机需要具备以下功能：能够成功用英语进行交流的自然语言处理(NLP)，能够存储其知道或听到的内容的知识表示(knowledge representation)，能够回答问题并且能够从存储的信息中提取新结论的自动推理(automated reasoning)，能够适应新场景并且能够检测和推断新模式的机器学习。 在整个的图灵测试中，还涉及视频信号，因此计算机需要更多的功能，用于对象感知的计算机视觉(computer vision)，以及用于物体操纵和运动控制的机器人技术(robotics)。AI研究人员一直致力于研究智能的基本原理，主要由上述六个学科所涵盖，而不是单纯的着眼于通过图灵测试，因为我们的目标通常并不是复制一个范例，例如，飞机并不是简单的模仿鸟。

定义2 ，”思维人性化“(thinking humanly)，遵循认知建模方法。 “令人兴奋的新奋斗目标是让计算机能够思考…让机器具有思维，在完整和字面意义上。”,"[自动化]与我们人类思维、活动（如作出决策，解决问题，学习…）相关的活动。”

定义3，“思维理性”(thinking rationally)，遵循“思想规律”的方法。 “使用计算模型研究智能。”，“使其能够感知，推理和行动的计算研究”。

定义4，“行为理性”(acting rationally)，遵循理性智能体方法。“计算智能是对智能agents设计的研究。”，“AI …关注人造机器中的智能行为。”理性智能体更多的遵循科学的发展，而不是基于人类行为或人类思维。因此重点关注理性智能体的一般原则及其构成要素。

我们列出了他们试图解答的基础和问题，如Russell和Norvig(2019)：

• 哲学，诸如“能用形式化（formal）的规则得出有效结论吗？”，“心智是如何从物理大脑中产生的？”，“知识从何而来？”，以及“知识是如何产生行动？”之类的问题;
• 数学，诸如“得出有效结论的形式化的规则是什么？”，“什么是可计算的？”，以及“我们如何用不确定的信息进行推理？”之类问题;
• 经济学，诸如“我们应该如何做出决策以最大化收益？”，“当其他人可能不参与的时候，我们该如何做？”， “如果未来收益可能很大，我们该如何做到这一点？”之类的问题;
• 神经科学，诸如“大脑如何处理信息？”之类的问题;
• 心理学，诸如“人类和动物如何思考和行动？”之类的问题;
• 计算机工程，诸如“我们如何构建高效计算机？”之类的问题;
• 控制理论和控制论，诸如“人造机器如何在他们自己的控制下运行？”之类的问题;
• 语言学，诸如“语言与思想是如何关联的？”之类的问题。

Russell和Norvig介绍了AI的历史:

AI的孕育期（1943-1955），
AI的诞生（1956），
早期的热情，伟大的期望（1952-1969），
一种现实(a dose of reality)（1966-1973），
基于知识的系统：力量的关键？ （1969-1979），
人工智能成为一个行业（1980年至今），
神经网络的回归（1986年至今），
人工智能采用科学方法（1987年至今），
智能agents出现（1995年至今），
大的数据集的可用性（2001年 - 现在）。

2.2 机器学习

机器学习研究如何从数据中学习并做出预测和/或决策。 引自Mitchell, T. (1997). Machine Learning. McGraw Hill.，“对于一个计算机程序，如果经性能度量P评判，关于任务T和性能度量P的经验E使得该程序在任务T中的表现有所提升，那么就可以说该程序从经验E中学习。”

通常我们将机器学习分为监督学习，无监督学习和强化学习。在监督学习中，数据有标签(label); 在无监督学习中，数据没有标签。 分类(Classification)和回归(Regression)是两种的监督学习问题，分别具有类别(categorical)和数值(numerical)输出。

无监督学习试图从没有标签的数据中提取信息，例如聚类(clustering)和密度估计(density estimation)。表征学习是一种经典的无监督学习。 然而，用监督学习训练深度神经网络也是一种表征学习。表征学习寻找(适当的)表征(representation)以尽可能多地保留关于原始数据的信息，同时，使用低维、稀疏、独立的表征以使这个表征比原始数据更简单或更易于访问(accessible),

深度学习或深度神经网络是一种特殊的机器学习方案，通常用于监督学习或无监督学习，并且可以与强化学习相结合，用于状态表示和/或函数逼近。 监督学习和无监督的学习通常是一次性的(one-shot)，短视的(myopic)，考虑即时奖励；而强化学习是连续的，有远见的，考虑到长期的累积奖励。

强化学习通常与顺序决策有关。 与监督学习和无监督学习相比，强化学习存在评估性反馈，但没有监督标签。与监督学习相比，强化学习还有其他挑战，如信用分配(credit assignment)，稳定性和探索。 强化学习是最优控制控制，运筹学和管理的亲属，也与心理学和神经科学有关。

机器学习是大数据，数据科学，预测建模，数据挖掘，信息检索等的基础，而且成了计算机视觉，自然语言处理，机器人等技术的关键要素。 概率论和统计学以及优化对于统计机器学习非常重要。 机器学习是AI的一个子集；然而，它正发展为在所有的AI领域都至关重要的一个子集。

机器学习算法由数据集，成本/损失函数，优化程序和模型组成。 数据集分为(无重叠的)训练集，验证集和测试集。 成本/损失函数度量模型性能，例如关于度量精度的，回归中的均方误差和(分类中的)分类错误率(classification error rate)。

熵(entropy)的概念对于损失函数的定义很重要。 对于具有分布$p$的随机变量$X$，熵是其不确定性的度量，定义为 $\mathbb{H}(X)$ 或$\mathbb{H}(p)$ ,
$$\mathbb{H}(X)\triangleq -\sum _{k=1}^{K}p(X=k){\log }_{2}p(X=k).\text{\hspace{1em}(1)}$$
对于二进制随机变量,$X\in \{0,1\}$，我们有 $p(X=1)=\theta$ 和 $p(X=0)=1-\theta$，
$$\mathbb{H}(X)=-\left[\theta {\log }_2\theta +(1-\theta ){\log }_2(1-\theta )\right].\text{\hspace{1em}(2)}$$
Kullback-Leibler divergence（KL-散度）或相对熵(relative entropy)，是衡量两种概率分布，$p$和$q$，的不相似性的一种方法，
$$\mathbb{K}\mathbb{L}(p\Vert q)\triangleq \sum _{k=1}^K{p}_k\log \frac{p_k}{q_k}\triangleq \sum _{k=1}^K{p}_k\log p_k-p_k\log q_k=-\mathbb{H}(p)+\mathbb{H}(p,q).\text{\hspace{1em}(3)}$$
其中，$\mathbb{H}(p,q)$是交叉熵。我们有 $\mathbb{K}\mathbb{L}(p,q)\triangleq -{\sum }_{k=1}^K{p}_k\log q_k$。请参考Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. The MIT Press.

训练误差(training error)是测量训练数据的误差，其最小化是一个优化问题。泛化误差(Generalization error)，或称测试误差(test error)，是测量新输入数据的误差，这是机器学习和优化的不同之处。机器学习算法试图缩小训练误差，并且减小训练误差与测试误差之间的差距(gap)。如果模型的训练误差较大，则称模型欠拟合(under-fitting);如果模型的训练误差和测试误差之间的gap较大，则称模型过拟合(over-fitting)。

模型的容量( model’s capacity)可以度量模型所能拟合的函数的范围。 奥卡姆剃刀原理(Ockham‘razor)表明，当具有相同的表现力时，我们应该首选最简单的模型。在训练误差和泛化误差vs.模型容量之间通常形成一种U形关系。 我们寻找实现低训练误差和训练误差与泛化误差之间低差距的最佳容量。偏差(Bias)测量估计值与真实值的期望离差(expected deviation)；而方差(variance)测量估计值与期望值的偏差(deviation)，或估计量的方差。随着模型容量的增加，偏差趋于减小，而方差趋于增大，在泛化误差与模型容量之间形成另一种U形关系。
我们试图找到最佳容量点，其中左侧为欠拟合，右侧为过拟合。 正则化(regularization)为成本函数添加惩罚项，以减小泛化误差，但不减小训练误差。 没有免费的午餐定理(no free lunch)表明没有通用的最佳模型或最佳的正则化方法。 这意味着深度学习可能不是解决某些问题的最佳模型。有模型参数，以及模型容量和正则化的超参数。交叉验证(cross-validation)用于调整超参数，以期在偏差和方差之间取得平衡，并选择最佳模型。

最大似然估计（Maximum likelihood estimation，MLE）是获得良好参数估计的常用方法。 对于数值下溢(numerical underflow)等问题，(通过取对数)将MLE中的乘积转换为求和以获得负对数似然(negative log-likelihood,NLL)。 MLE相当于最小化KL散度，即最小化经验分布 (由训练数据定义)与模型分布之间的差异。 最小化两个分布之间的KL散度对应于最小化两分布之间的交叉熵。 简而言之，似然估计的最大化变为负对数似然(NLL)的最小化，或等效地，交叉熵的最小化。

梯度下降(gradient descent)是解决优化问题的常用方法。 随机梯度下降(Stochastic gradient descent)通过每次随机选用单个样本来更新下降梯度，并且（小批量梯度下降）通常使用小批量(Mini-batch)（的训练集样本来更新模型参数）。

重要性采样是一种通过从某个(与待估计分布)不同的分布采样，来估计一个特定分布的属性的技术。用于降低估计的方差，或者用于从难以抽样的特定分布中抽样。

有机器学习算法的数学分析框架。 Kolmogorov复杂度或算法复杂度研究了Ockham剃刀中的简单概念。 在概率近似正确（probably approximately correct，PAC）学习中，学习算法旨在选择泛化函数，以高概率实现低泛化误差.VC维度测量二元分类器的容量。

2.3 深度学习

深度学习区别于“shallow”学习。对于许多机器学习算法，例如线性回归，逻辑回归，支持向量机（SVM），决策树和boosting(将弱分类器组装成一个强分类器)，只有输入层和输出层，并且输入可以在训练之前通过手动特征工程变换。在深度学习中，输入层和输出层之间有一个或多个隐藏层，在每一层(输入层除外)中，计算前一层神经元的加权和，作为该层每个神经元的输入；然后通常将非线性变换或激活函数，如logistic、tanh或更常见的ReLU,应用于单元的输入，以获得来自前一层的输入的新表示。

在层与层之间的链接上有权重。 在计算了从输入流向输出的前向传播之后，在输出层和每个隐藏层，我们可以向后计算误差导数，并向输入层反向传播梯度，以便可以更新权重以优化损失函数。

前馈深度神经网络或多层感知机（multilayer perceptron, MLP）利用每一层简单的函数组合成复杂的数学函数，从而将一组输入值映射到输出值。卷积神经网络(CNN) 是一种前馈神经网络，具有卷积层、池化层和全连接层。 CNN被设计用于处理具有multiple arrays(网格化)的数据，例如彩色图像，语言，音频谱图和视频，这受益于此类信号的属性：局部连接，共享权重，池化，多层结构，并且受到了视觉神经科学中简单细胞和复杂细胞的启发。多层网络结构。

ResNets旨在通过添加快捷连接来学习关于层输入的残差函数，以此简化非常深的神经网络的训练。循环神经网络（RNN）通常用于处理序列数据，如语音和语言，逐个元素，隐藏单元用于存储过去元素的历史。当在正向计算的时间展开时，RNN可被视为多层神经网络，所有层共享相同的权重。 RNN很难长时间存储信息，梯度可能会消失。 学者提出了长期短期记忆网络（LSTM）和门控循环单元（GRU）来解决这些问题，其中门控机制通过循环细胞来操纵信息。 梯度反向传播或其变体可用于训练上述所有深度神经网络。

Dropout是一种正则化策略，通过从原始网络中随机删除非输出单元来训练子网络集合。 批标准化(Batch normalization)和层标准化(layer normalization)旨在提高训练效率。

深度神经网络从原始输入中自动学习representations,以恢复许多自然信号中的组成层次结构，即，高层次的特征由低层次的特征组成。如在图像中，the hierarch of objects, parts, motifs, and local combinations of edges. 分布式表示是深度学习的核心思想，这意味着许多特征可以代表每个输入，并且每个特征可以代表许多输入。 深度分布式表示的指数优势可以应对维度诅咒的指数挑战。端到端的训练是指学习模型使用原始输入（通常没有手动特征工程）来生成输出，例如，AlexNet利用原始像素进行图像分类，Graves等人用音频数据的傅里叶变换进行语音识别，Seq2Seq用原始句子做机器翻译，DQN利用原始像素和得分来玩游戏。

人们正在努力设计新的神经网络架构，如胶囊网络(capsules)。 还在努力设计没有神经网络的深度机器学习架构，如DeepForest。

2.4 强化学习

我们在本节简要介绍强化学习的背景，作为迷你教程。为了深入理解深度强化学习，必须对强化学习有一个很好的理解。Deep RL是一种特殊类型的RL，用深度神经网络进行状态表示(state representation)和/或用深度神经网络进行值函数、策略、转移模型或奖励函数的函数近似。Silver(2015)¹是强化学习的简明教程。

Sutton和Barto(2018)²在每章末尾提供了强化学习书目和历史评论。 Russell和Norvig（2009）在第21章强化学习中提供了参考书目和历史记录。 Barto（2018）讨论了强化学习的简史。

首先我们介绍一些RL术语。 读完本章剩余小节，这些术语将变得更加清晰。 我们将它们集中放在这里，方便读者检查。

预测问题或策略评估是计算策略的状态值函数(state-value function)或动作值函数(action-value function)。 控制问题是找到最优策略。 规划(Planning)是使用模型构造值函数或策略。

同策略(on-policy)方法评估或改进行为策略(behaviour policy)，例如，SARSA使动作值函数符合当前策略，即SARSA基于采样自相同策略的样本来评估策略，然后根据动作值函数采用贪心算法优化策略。在异策略(off-policy)方法中，agent可能遵循不相关的行为策略，来学习最优值函数/策略。例如，Q-learning试图直接找到最优策略的动作值，该策略不必是生成数据的策略，即Q-learning得到的策略与生成样本的策略通常是不同的策略。on-policy和off-policy的概念可以理解为同一策略和不同策略。
（译者注：此处on-policy和off-policy的介绍不够清晰，补充理解：https://www.zhihu.com/question/57159315 ）

2.4.1 Problem Setup

RL智能体(agent)随时间的推移与环境(environment)交互。在每个时间步($t$，智能体收到状态空间$\mathcal{S}$中的一个状态(state) $s_t$；然后遵循策略(policy) $\pi \left(a_t|s_t\right)$，从动作空间$\mathcal{A}$中选择一个动作(action) $a_t$，即从状态$s_t$映射到动作$a_t$，该策略即为智能体的行为(behavior)；根据环境dynamic或模型，智能体收到一个标量奖赏(reward) $r_t$，并且转移到下一个状态$s_{t+1}$,for reward function $\mathcal{R}(s,a),$ and, state transition probability $\mathcal{P}\left(s_{t+1}|s_t,a_t\right)$, respectively。在一个episodic(由许多片段组成的)问题中，这个过程一直持续到智能体到达终止状态(terminal state)，然后重新开始。回报(return)是奖赏的折扣累计值，折扣因子$\gamma \in (0,1]$，
$$R_t=\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k}.\text{\hspace{1em}(4)}$$
智能体的目标是最大化这种来自每个状态的长期回报的期望，此问题是在离散状态空间和离散动作空间set up的，将其扩展到连续空间并不困难。在部分可观测的环境中，智能体不能完全观测state，但有observations。

当RL问题满足马尔可夫性质( Markov property)时, 即未来仅取决于当前的状态和动作，而去过去无关时,它可以被表述为由5元组$(\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma )$定义的马尔可夫决策过程(Markov decision process，MDP)。 有系统模型时，我们使用动态规划方法：策略评估来计算策略的值/动作值函数，值迭代和策略迭代以找到最优策略。没有模型时，我们采用RL方法。有模型时RL也能work。RL的环境可以是 多摇臂赌博机、MDP、部分可观测MDP(partially observable MDP，POMDP)、游戏等。

2.4.2 值函数

值函数是对预期的未来奖赏的折扣累计值的预测，用于衡量每个状态或状态-动作对的好坏程度。状态值，
$$v_{\pi }(s)=\mathbb{E}\left[R_t|s_t=s\right],\text{ where, }{R}_t=\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k}，\text{\hspace{1em}(5)}$$
是从状态$s$开始跟随策略$\pi$的期望回报。动作值，
$$q_{\pi }(s,a)=\mathbb{E}\left[R_t|s_t=s,a_t=a\right]，\text{\hspace{1em}(6)}$$
是在状态$s$下选择动作$a$,然后跟随策略$\pi$的期望回报。值函数$v_{\pi }(s)$分解成Bellman方程：
$$v_{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime },r}p\left(s^{\prime },r|s,a\right)\left[r+\gamma v_{\pi }\left(s^{\prime }\right)\right].\text{\hspace{1em}(7)}$$
最优状态值，
$$v_{\ast }(s)=\underset{\pi }{\max }{v}_{\pi }(s)=\underset{a}{\max }{q}_{{\pi }^{\ast }}(s,a)，\text{\hspace{1em}(8)}$$
是所有策略在状态$s$可实现的最大状态值，把它分解为Bellman方程：
$$v_{\ast }(s)=\underset{a}{\max }\sum _{s^{\prime },r}p\left(s^{\prime },r|s,a\right)\left[r+\gamma v_{\ast }\left(s^{\prime }\right)\right].\text{\hspace{1em}(9)}$$
动作值函数$q_{\pi }(s,a)$分解为Bellman方程：
$$q_{\pi }(s,a)=\sum _{s^{\prime },r}p\left(s^{\prime },r|s,a\right)\left[r+\gamma \sum _{a^{\prime }}\pi \left(a^{\prime }|s^{\prime }\right)q_{\pi }\left(s^{\prime },a^{\prime }\right)\right].\text{\hspace{1em}(10)}$$
最优动作值函数，
$$q_{\ast }(s,a)=\underset{\pi }{\max }{q}_{\pi }(s,a)，\text{\hspace{1em}(11)}$$
是所有策略在状态$s$和动作$a$可实现的最大动作值，把它分解为Bellman方程：
$$q_{\ast }(s,a)=\sum _{s^{\prime },r}p\left(s^{\prime },r|s,a\right)\left[r+\gamma \underset{a^{\prime }}{\max }{q}_{\ast }\left(s^{\prime },a^{\prime }\right)\right].\text{\hspace{1em}(12)}$$
以最短路径问题为例，在图论(graph theory)中，单源最短路径问题是找到一对节点之间的最短路径，以使路径中边缘的权重之和最小。在RL中，状态就是当前的节点，在每个节点处，链接两个相邻节点的是动作。转移模型表明，选择一个链接跟随后，智能体会转移到相邻节点。然后，奖赏是链接weight/cost/distance的负值。如果是一个片段任务，折扣因子可以是$\gamma =1$。目标是找到最大化总cost负值的路径，即最小化总distance。。最优策略是选择最优临近节点以实现最短路径；并且，对于每个状态/节点，最优值是从该节点到目的地的最短距离。 Dijkstra’s算法是一种有效的算法，具有图的信息，包括节点，边和权重。RL可以在model-free(无模型)方法中work，没有全局图信息时，RL可以根据某种策略在图中wander。 RL算法比Dijkstra算法更通用，尽管具有全局图信息时，Dijkstra算法非常有效。

2.4.3 探索与利用(Exploration vs. Exploitation)

RL智能体需要在探索新策略和利用当前最优策略之间进行权衡，这是RL的一个基本困境。这里我们介绍一个简单的方法，$ϵ$-greedy算法，其中$ϵ\in (0,1)$，通常是一个接近0的小数值。在$ϵ$-greedy中，智能体在当前状态$s$以概率$1-ϵ$选择贪婪动作$a=\arg {\max }_{a\in \mathcal{A}}Q(s,a)$，以概率$ϵ$选择随机动作。也就是说，智能体以概率$1-ϵ$利用当前值函数估计值，并以概率$ϵ$进行探索。
我们将在第7章中讨论更多关于探索与利用困境的内容，包括几个原则：
朴素探索(Naive Exploration)，如$ϵ$-greedy，乐观初始估计(Optimistic Initialization)，置信区间上界(Upper Confidence Bounds)，概率匹配（Probability Matching)，信息状态搜索(Information State Search)。这些都是在多臂老虎机设定中发展起来的，但适用于RL问题。

2.4.4 动态规划

动态规划(dynamic programming, DP)是解决最优子结构和重叠子问题的一般方法。 MDP满足这些属性，其中，Bellman方程给出递归分解，并且值函数可存储，子解可重用。 DP假设充分了解MDP的转移和奖赏模型。 预测问题是评估给定策略的值函数，控制问题是找到最优值函数和/或最优策略。
迭代策略评估是一种评估给定策略$\pi$的方法。 它迭代地应用Bellman expectation backup,
$$v_{k+1}(s)=\sum _{a\in \mathcal{A}}\pi (a|s)\left[\mathcal{R}(s,a)+\gamma \sum _{s^{\prime }\in \mathcal{S}}\mathcal{P}\left(s^{\prime }|s,a\right)v_k\left(s^{\prime }\right)\right].\text{\hspace{1em}(13)}$$
因此，在每次迭代$k+1$时，对于所有的状态$s\in \mathcal{S}$，用其后继状态$v_k\left(s^{\prime }\right)$的值函数来更新$v_{k+1}(s)$。值函数将收敛于$v_{\pi }(s)$,即策略$\pi$的值函数。
策略迭代(policy iteration, PI)交替使用策略评估和策略改进，以生成一系列改进策略。在策略评估中，评估当前策略的值函数以获得$v_{\pi }$。在策略改进中，当前值函数被用于生成更好的策略。例如，根据值函数$v_{\pi }$采用贪婪策略选择动作。这种策略迭代过程将会收敛到最优策略和值函数。
我们可以修改策略迭代步骤，使其在收敛之前停止。广义迭代策略(GPI)可以由任意策略评估方法和任意策略改进方法组成。
值迭代(value iteration)寻找最优策略，它迭代的应用Bellman optimality backup,
$$v_{\ast }(s)=\underset{a}{\max }\mathcal{R}(s,a)+\gamma \sum _{s^{\prime }\in \mathcal{S}}\mathcal{P}\left(s^{\prime }|s,a\right)v_k\left(s^{\prime }\right).\text{\hspace{1em}(14)}$$
在每次迭代$k+1$，对于所有的状态$s\in \mathcal{S}$，用$v_k\left(s^{\prime }\right)$的来更新$v_{k+1}(s)$。这种同步backup将收敛到最优策略的值函数。 我们还有异步DP，以及近似DP。
我们在方程(7)中有值函数的Bellman方程。 Bellman算子被定义为，
$$\left(T^{\pi }v\right)(s)\doteq \sum _a\pi (a|s)\sum _{s^{\prime },r}p\left(s^{\prime },r|s,a\right)\left[r+\gamma v_{\pi }\left(s^{\prime }\right)\right].\text{\hspace{1em}(15)}$$
则有，TD fix point,
$$v_{\pi }=T^{\pi }{v}_{\pi }.\text{\hspace{1em}(16)}$$
我们可以定义Bellman expectation backup算子的矩阵形式，
$$T^{\pi }(v)=\mathcal{R}+\gamma {\mathcal{P}}^{\pi }v,\text{\hspace{1em}(17)}$$
以及 Bellman optimality backup算子，
$$T^{\ast }(v)=\underset{a\in \mathcal{A}}{\max }{\mathcal{R}}^a+\gamma {\mathcal{P}}^{a}v.\text{\hspace{1em}(18)}$$
我们可以证明这些运算符是 contractions with fixed points，这有助于证明策略迭代、值迭代和其他策略迭代算法的收敛性。有关详细信息，请参见Silver(2015)，Sutton和Barto(2018)以及Bertsekas和Tsitsiklis(1996)。

2.4.5 蒙特卡罗

蒙特卡罗方法从完整的经验episodes中学习并使用采样方法进行估计，而不是假设已知转移或奖赏模型的知识。 蒙特卡罗方法仅适用于episodic(片段的)任务。
使用蒙特卡罗方法进行策略评估时，我们使用经验平均return而不是预期return进行评估。 根据大数定律，估计的值函数收敛于策略的值函数。
同策略(on-policy)蒙特卡洛控制遵循广义的策略迭代方案。对于策略评估，它使用蒙特卡洛策略评估来确定动作值。对于策略改进，它采用$ϵ\text{ -greedy }$进行策略改进。可以证明， Greedy in the limit with infinite exploration (GLIE) Monte-Carlo control收敛于最优值函数。
在异策略(off-policy)学习中,我们根据行为策略评估目标策略。通过off-policy，我们可以从人类或其他智能体的观测中学习，重用旧策略的经验，同时遵循探索策略学习最优策略，and,根据一种策略的经验学习多种策略。
我们可以对off-policy蒙特卡洛方法使用重要性采样，通过在整个episode中乘以重要性采样校正权重，以使用行为策略生成的经验评估目标策略。但这可能会显着增加variance。

2.4.6 时序差分学习

时序差分(temporal difference,TD)学习是RL的核心。TD学习通常指Sutton (1988) 提出的值函数评估学习方法。Q-learning和SARASA就是时间差分控制方法。
TD learning直接从经验中根据TD误差学习值函数$V(s)$，以无模型、在线和完全增量的方式自举(bootstrapping)。TD学习是一个预测问题，更新规则是，
$$V(s)\leftarrow V(s)+\alpha \left[r+\gamma V\left(s^{\prime }\right)-V(s)\right].\text{\hspace{1em}(19)}$$
其中，$\alpha$是学习率，$r+\gamma V\left(s^{\prime }\right)-V(s)$是TD误差。算法1给出了TD learning的伪代码。确切地说，它是tabular TD(0)学习，其中“0”表示它基于one-step returns。
Bootstrapping根据TD更新规则中的subsequent估计来估计状态或动作值函数，这在RL中很常见，如TD learning，Q-learning和SARSA。Bootstrapping方法通常学习的更快，并且能够使学习在线和持续。Bootstrapping方法不是真正的梯度下降，因为它的target取决于要估计的value。半梯度下降的概念后面介绍（Sutton and Barto,2018）。

Input: the policy $\pi$ to be evaluated
output : value function $V$

---

initialize $V$ arbitrarily, e.g., to 0 for all states
for $eachepisode$ do
    initialize state $s$
    for each $stepofepisode$, state $s$ is $notterminal$ do
        $a\leftarrow$ action given by $\pi$ for $s$
        take action $a$, observe $r,s^{\prime }$
        $V(s)\leftarrow V(s)+\alpha \left[r+\gamma V\left(s^{\prime }\right)-V(s)\right]$
        $s\leftarrow s^{\prime }$
    end
end

---

Algorithm 1: TD learning, adapted from Sutton and Barto (2018)

Output: action value function $Q$

---

initialize $Q$ arbitrarily, e.g., to 0 for all states, set action value for terminal states as 0
for $eachepisode$ do
initialize state $s$
for $eachstepofepisode$, state $s$ is $notterminal$ do
        $a\leftarrow$ action for $s$ derived by $Q$ ，e.g.，$ϵ$-greedy
        take action $a$, observe $r,s^{\prime }$
        $a^{\prime }\leftarrow$ action for $s^{\prime }$ derived by $Q$ ，e.g.，$ϵ$-greedy
        $Q(s,a)\leftarrow Q(s,a)+\alpha \left[r+\gamma Q\left(s^{\prime },a^{\prime }\right)-Q(s,a)\right]$
        $s\leftarrow s^{\prime },a\leftarrow a^{\prime }$
    end
end

---

Algorithm 2: SARSA, adapted from Sutton and Barto (2018)

Output: action value function $Q$

---

for $eachepisode$ do
    initialize state $s$
for $eachstepofepisode$, state $s$ is $notterminal$ do
        $a\leftarrow$ action for $s$ derived by $Q$ ，e.g.，$ϵ$-greedy
        take action $a$, observe $r,s^{\prime }$
        $Q(s,a)\leftarrow Q(s,a)+\alpha \left[r+\gamma {\max }_{a^{\prime }}Q\left(s^{\prime },a^{\prime }\right)-Q(s,a)\right]$
        $s\leftarrow s^{\prime }$
    end
end

---

Algorithm 3: Q-learning, adapted from Sutton and Barto (2018)

SARSA,代表state，action，reward,(next) state, (next) action，是一种搜寻最优策略的on-policy控制方法，具有更新规则，
$$Q(s,a)\leftarrow Q(s,a)+\alpha \left[r+\gamma Q\left(s^{\prime },a^{\prime }\right)-Q(s,a)\right].\text{\hspace{1em}(20)}$$
算法2 给出了tabular SARSA即tabular SARSA(0)的伪代码。
Q-learning是一种搜寻最优策略的off-policy控制方法。Q-learning采用如下更新规则学习动作值函数，
$$Q(s,a)\leftarrow Q(s,a)+\alpha \left[r+\gamma \underset{a^{\prime }}{\max }Q\left(s^{\prime },a^{\prime }\right)-Q(s,a)\right].\text{\hspace{1em}(21)}$$
Q-learning采用贪心算法改进策略，算法3给出了Q-learning的伪代码，确切的说是tabular Q(0) learning的伪代码。
TD-learning，Q-learning和SARSA在某些条件下会收敛至最优动作值函数。 根据最优动作值函数，我们可以得到最优策略。

2.4.7 多步拔靴法

上述算法称为TD(0)，Q(0)和SARSA(0)，采用单步return进行学习。我们在前面的概述中已经提供了多步return的变体。在$n$-step更新中$V(s_t)$采用$n$-step return进行更新，定义为，
$$r_t+\gamma r_{t+1}+\cdots +{\gamma }^{n-1}{r}_{t+n-1}+{\gamma }^{n}V\left(s_{t+n}\right).\text{\hspace{1em}(22)}$$

来自backward view的eligibility trace提供了在线的增量实现，产生了TD($\lambda$)，Q($\lambda$)和SARSA($\lambda$)算法，其中$\lambda \in [0,1]$。TD(1)与蒙特卡罗方法相同。 eligibility trace是一种短期记忆，通常持续在一个episode中，通过影响加权向量来辅助学习过程。 加权向量(weight vector)是一个长期记忆，存在于系统的整个持续时间，决定了估计的value。 eligibility trace有助于解决长期延迟奖励(long-delayed reward)和非马尔可夫任务的问题。
TD($\lambda$)使用eligibility trace和衰减参数$\lambda$，统一了单步TD预测TD(0)和蒙特卡罗方法TD(1)，用于预测算法。De Asis等人(2018)统一了多步TD控制算法。
DP，MC和TD的比较
在下文中，我们基于Silver(2015)和Sutton and Barto(2018)比较动态规划(DP)，蒙特卡罗(MC)和时间差分(TD)学习。
DP需要模型; TD和MC无模型。 DP和TD bootstrap; MC没有。 TD和MC使用sample backups(样本备份)，DP和穷举搜索(exhaustive search)使用full backups。 DP使用单步backups; TD可与一步或多步backups配合使用; MC和穷举搜索使用深度backups，直到episode终止。
TD可以在连续的环境中从不完整的序列中在线学习。MC在episodic环境中从完整的序列中学习。TD方差小、有偏差、通常比MC更高效，对初始值敏感。TD(0)收敛于策略的值函数，采用值函数近似(function approximation)时可能会发散。MC方差大、无偏差、易于理解和使用、对初始值不敏感。MC具有良好的收敛性，即使有函数近似也能收敛。
TD利用了马尔可夫性质，因此在马尔可夫环境中更有效。MC没有利用马尔可夫性质，因此通常在非马尔可夫环境中更有效。

Full Backup (DP)	Sample Backup
迭代策略评估：$v(s)\leftarrow \mathbb{E}\left[r+\gamma v\left(s^{\prime }\right)s\right]$	TD learning：$v(s)\stackrel{\alpha }{\leftarrow }r+\gamma v\left(s^{\prime }\right)$
Q 策略迭代：$Q(s,a)\leftarrow \mathbb{E}\left[r+\gamma Q\left(s^{\prime },a^{\prime }\right)s,a\right]$	SARSA：$Q(s,a)\stackrel{\alpha }{\leftarrow }r+\gamma Q\left(s^{\prime },a^{\prime }\right)$
Q 值迭代：$Q(s,a)\leftarrow \mathbb{E}\left[r+\gamma {\max }_{a^{\prime }\in \mathcal{A}}Q\left(s^{\prime },a^{\prime }\right)s,a\right]$	Q-learning ：$Q(s,a)\stackrel{\alpha }{\leftarrow }r+\gamma {\max }_{a^{\prime }\in \mathcal{A}}Q\left(s^{\prime },a^{\prime }\right)$

表1：比较DP和TD学习，其中，$x\stackrel{\alpha }{\leftarrow }y\doteq x\leftarrow \alpha (y-x)$。

2.4.8 基于模型的RL

Sutton(1990)提出的Dyna-Q算法将learning、acting和planning整合在一起，不仅可以从实际经验中学习，还可以过学习到的模型的仿真轨迹进行规划。 learning使用来自环境的真实经验; planning使用模型模拟的经验。算法4给出了 tabular Dyna-Q的伪代码。我们将在第6章中讨论更多有关基于模型的RL的信息。

2.4.9 函数近似

我们讨论上面的表格(tabular)案例，其中值函数或策略以tabular形式存储。当状态或动作空间很大或连续时，函数逼近是一种概括的(generalization)方法。函数逼近的目的是从函数的示例中概括出构造整个函数的approximate。这通常是监督学习中的概念，在机器学习，模式识别和统计曲线拟合等领域进行研究; 强化学习中的函数逼近通常将每个backup视为训练示例，同时要考虑非平稳性(nonstationarity)、bootstrapping和延迟目标等新问题。线性函数逼近是一种流行的选择，部分原因在于其理想的理论属性，尤其是在deep Q-Network出现之前。然而，强化学习和神经网络的整合可以追溯到很久以前(Sutton and Barto, 2018; Bertsekas and Tsitsiklis,1996; Schmidhuber, 2015)。
算法5给出了用函数逼近的TD(0)的伪代码。
算法5用函数逼近表示TD的伪代码。 V是近似值函数，w是值函数权重向量，RV是近似值函数相对于权重向量的梯度，其根据更新规则更新，
$$\mathbf{w}\leftarrow \mathbf{w}+\alpha \left[r+\gamma \hat{v}\left(s^{\prime },\mathbf{w}\right)-\hat{v}(s,\mathbf{w})\right]\nabla \hat{v}(s,\mathbf{w}).\text{\hspace{1em}(23)}$$
off-policy、function approximation、bootstrapping三者组合时，可能会导致算法不稳定和不收敛，这被称为致命三元组问题(Sutton and Barto,2018)。然而这三个元素都是必不可少的：function approximation使算法具备扩展能力和泛化能力，bootstraping用于计算和数据效率，off-policy学习用于分离行为策略和目标策略。那么什么是导致RL算法不稳定的根本原因呢？ Learning or sampling
is not, since dynamic programming suffers from divergence with function approximation; exploration, greedification, or control is not, since prediction alone can diverge; local minima or complex non-linear function approximation is not, since linear function approximation can produce instability (Sutton, 2016). It is unclear what is the root cause for instability – each single factor mentioned above is not – there are still many open problems in off-policy learning (Sutton and Barto, 2018).

表2列出了解决各种问题的不同算法(Sutton,2016)。 ADP算法指的是近似动态规划算法，如具有函数逼近的策略评估、策略迭代和值迭代。最小二乘时序差分算法(LSTD)直接在批处理模式下计算TD fix-point。LSTD是数据高效的，但具有平方时间复杂度。LSPE扩展了LSTD。Fitted-Q算法以批处理模式学习动作值。残差梯度算法最小化Bellman误差。Gradient-TD方法是真正的梯度算法，在projected Bellman err(PBE)中执行SGD，在off-policy和非线性函数逼近下稳健的收敛。Expected SARSA和SARSA具有相同的收敛保证，而前者方差更小。Emphatic-TD emphasizes some updates and de-emphasizes others by reweighting, improving computational efficiency, yet being a semi-gradient method. 有关详细信息，请参阅Sutton和Barto(2018).Du等人提出方差减小技术用于策略评估，以实现快速收敛。Liu等人研究了proximal 梯度TD learning。White and White 对线性TD方法进行了实验比较，并对其实际应用提出了建议。Jin等人(2018)研究了Q-learning的样本效率。Lu等人研究了non-delusional Q-learning和价值迭代。

2.4.10 策略优化

与value-based方法(如TD learning和Q-learning)相比，policy-based方法直接优化策略$\pi (a|s;\mathbf{\theta })$(使用函数逼近)，并且通过梯度上升来更新参数$\mathbf{\theta }$。与value-based的方法相比，policy-based的方法方法通常具有更好的收敛性、在高纬度或者连续动作空间中更有效，并且可以学习随机策略。然而policy-based方法通常会收敛到局部最优，评估效率低，而且方差较大。随机策略很重要，因为一些问题只有随机最优策略，例如，在石头剪刀布游戏中，每个玩家的最佳策略都是以1/3的概率采取每个动作。
对于一个可微分的策略$\pi (a|s;\mathbf{\theta })$，只要不等于零，我们就可以解析的计算策略梯度，
$${\nabla }_{\mathbf{\theta }}\pi (a|s;\mathbf{\theta })=\pi (a|s;\mathbf{\theta })\frac{{\nabla }_{\mathbf{\theta }}\pi (a|s;\mathbf{\theta })}{\pi (a|s;\mathbf{\theta })}=\pi (a|s;\mathbf{\theta }){\nabla }_{\mathbf{\theta }}\log \pi (a|s;\mathbf{\theta }).\text{\hspace{1em}(24)}$$
我们称${\nabla }_{\mathbf{\theta }}\log \pi (a|s;\mathbf{\theta })$为score function 或似然比。 策略梯度定理 (Sutton, 2000) 指出，对于可微分策略$\pi (a|s;\mathbf{\theta })$，策略梯度是，
$${\mathbb{E}}_{{\pi }_{\mathbf{\theta }}}\left[{\nabla }_{\mathbf{\theta }}\log \pi (a|s;\mathbf{\theta })Q^{{\pi }_{\mathbf{\theta }}}(s,a)\right].\text{\hspace{1em}(25)}$$
为简单起见，我们在下面的值函数中省略了${\pi }_{\mathbf{\theta }}$。
通过利用return $R_t$作为$Q(s_t,a_t)$的无偏样本，REINFORCE (Williams, 1992) 更新$\mathbf{\theta }$，方向为，
$${\nabla }_{\mathbf{\theta }}\log \pi \left(a_t|s_t;\mathbf{\theta }\right)R_t.\text{\hspace{1em}(26)}$$
通常从return中减去基线$b_t(s_t)$以减小梯度估计的方差，同时保持其无偏性，以产生梯度方向，
$${\nabla }_{\mathbf{\theta }}\log \pi \left(a_t|s_t;\mathbf{\theta }\right)(Q(s_t,a_t)-b_t(s_t)).\text{\hspace{1em}(27)}$$
使用$V(s_t)$作为基线$b_t(s_t)$，我们有advantage function，
$$A(s_t,a_t)=Q(s_t,a_t)-V(s_t).\text{\hspace{1em}(28)}$$
算法6 给出了REINFORCE算法的伪代码。

在演员-评论家(actor-critic)算法中，critic更新动作值函数参数，并且actor根据critic建议的方向更新策略参数。 算法7给出了单步actor-critic算法的伪代码。
正如Silver(2015)总结的那样，策略迭代有多种形式：${\nabla }_{\mathbf{\theta }}\log \pi \left(a|s;\mathbf{\theta }\right)R_t$ for REINFORCE，${\nabla }_{\mathbf{\theta }}\log \pi (a|s;\mathbf{\theta })Q(s,a;\mathbf{w})$ for actor-critic,${\nabla }_{\mathbf{\theta }}\log \pi (a|s;\mathbf{\theta })A(s,a;\mathbf{w})$ for advantage actor-critic,${\nabla }_{\mathbf{\theta }}\log \pi (a|s;\mathbf{\theta })\delta$ for TD actor-critic, ${\nabla }_{\mathbf{\theta }}\log \pi (a|s;\mathbf{\theta })\delta e$ for TD($\lambda$) actor-critic, $G_{\mathbf{\theta }}\mathbf{w}$ for自然梯度下降，其中$G_{\mathbf{\theta }}={\mathbb{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\mathbf{\theta }}\log \pi (a|s;\mathbf{\theta }){\nabla }_{\mathbf{\theta }}\log \pi (a|s;\mathbf{\theta }{)}^T\right]$是Fisher信息矩阵；而且critic可能使用蒙特卡洛或TD learning进行政策评估来估计价值函数$Q,A$或$V$。

2.4.11 Deep RL

当我们使用深度神经网络来表示state或observation，或近似强化学习的任何部分：值函数$\hat{v}(s;\mathbf{\theta })$或$\hat{q}(s,a;\mathbf{\theta })$、策略$\pi (a|s;\mathbf{\theta })$和模型（状态转移函数和reward函数）时，就得到了深度强化学习(deep RL)方法。这里，参数$\mathbf{\theta }$是深度神经网络中的权重。当我们使用“浅”模型，如线性函数，决策树，tile编码等作为函数逼近器时，我们得到“浅”RL，参数$\mathbf{\theta }$是这些模型中的权重参数。注意，浅模型（例如决策树）可以是非线性的。deep RL和“浅”RL之间的显著区别是使用何种函数逼近器。这类似于深度学习和“浅层”机器学习之间的区别。我们通常利用随机梯度下降来更新deep RL中的权重参数。当off-policy、函数逼近(尤其是非线性函数逼近)和bootstrapping结合在一起时，可能会使算法不稳定或发散(Tsitsiklis and Van Roy, 1997).。然而，最近的工作如deep Q-learning和AlphaGo训练稳定，并且取得了出色的成果。有许多研究致力于正品非线性函数逼近控制的收敛性，如 Dai et al. (2018b); Nachum et al. (2018).

2.4.12 小结

当对环境的observation满足马尔可夫性质时，RL问题被形式化的表述为一个MDP问题。 MDP由5元组定义$(\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma )$。 RL中的一个核心概念是value function。Bellman方程是建立RL算法的基石。时序差分学习算法是评估/预测值value function的基础。控制算法寻找最优策略。Policy-based方法最近变得流行起来。RL算法可以基于值函数和/或策略，model-free或model-based，on-policy或off-policy，有函数逼近或者没有，具有样本备份(TD和MC)或完整备份(DP和穷举搜索)，以及备份的深度，单步return(TD(0)和DP)或多步return(TD($\lambda$),MC,穷举搜索)。当结合off-policy，函数逼近和bootstrapping时，我们面临不稳定和发散(Tsitsiklis and Van Roy, 1997)，致命三元组问题(Sutton和Barto,2018)。我们已经为线性函数逼近建立了理论保证，例如Gradient-TD (Sutton et al., 2009a;b; Mahmood et al., 2014), Emphatic-TD (Sutton et al., 2016) and Du et al. (2017)。当RL与深度神经网络集成时，无论是为了representation还是为了函数逼近，我们都有deep RL。Deep Q-Network和AlphaGo等深度RL算法可以稳定学习并获得惊人的效果。

2.5 资源

我们在下面介绍一些deep RL的资源。We maintain a blog titled Resources for Deep Reinforcement Learning at https://medium.com/@yuxili/.
Sutton and Barto’s RL book (Sutton and Barto, 2018) covers fundamentals and reflects new progress,e.g., in deep Q-network, AlphaGo, policy gradient methods, as well as in psychology and neuroscience. David Silver’s RL course (Silver, 2015) and Sergey Levine’s Deep RL course (Levine,2018) are highly recommended.
Goodfellow et al. (2016) is a recent deep learning book. Bishop (2011), Hastie et al. (2009), and Murphy (2012) are popular machine learning textbooks. James et al. (2013) is an introduction book for machine learning. Domingos (2012), Zinkevich (2017), and Ng (2018) are about practical machine learning advices. See Ng (2016b) and Schulman (2017) for practical advices for deep learning and deep RL respectively.
There are excellent summer schools and bootcamps, e.g., Deep Learning and Reinforcement Learning Summer School: 2018 at https://dlrlsummerschool.ca, 2017 at https://mila.umontreal.ca/en/cours/deep-learning-summer-school-2017/; Deep Learning Summer School: 2016 at https://sites.google.com/site/deeplearningsummerschool2016/, and, 2015 at https://sites.google.com/site/deeplearningsummerschool/; and, Deep RL Bootcamp: at https://sites.google.com/view/deep-rl-bootcamp/.
Common benchmarks for general RL algorithms are Atari games in the Arcade Learning Environment (ALE) for discrete control, and simulated robots using the MuJoCo physics engine in OpenAI Gym for continuous control.
The Arcade Learning Environment (ALE) (Bellemare et al., 2013; Machado et al., 2017) is a framework composed of Atari 2600 games to develop and evaluate AI agents. OpenAI Gym, at https://gym.openai.com, is a toolkit for the development of RL algorithms, consisting of environments, e.g., Atari games and simulated robots, and a site for the comparison and reproduction of results. MuJoCo, Multi-Joint dynamics with Contact, at http://www.mujoco.org, is a physics engine. DeepMind Lab (Beattie et al., 2016) is a first-person 3D game platform, at https://github.com/deepmind/lab. DeepMind Control Suite (Tassa et al., 2018) provides RL environments with the MuJoCo physics engine, at https://github.com/deepmind/dm_control. Dopamine (Bellemare et al., 2018) is a Tensorflow-based RL framework from Google AI. ELF, at https://github.com/pytorch/ELF, is a platform for RL research (Tian et al.,2017). ELF OpenGo is a reimplementation of AlphaGo Zero/Alpha Zero using the ELF framework.

Part 1：核心要素

3 值函数

3.1 Deep Q-Learning

3.2 分布式值函数

General Value Functional

4 策略

5 奖赏

6 模型

7 探索与利用

8 表示

Part 2：重要机制

9 注意力与记忆

10 无监督学习

11 分层RL

12 多智能体RL

13 Relational RL

14 元学习

Part 3：应用

游戏

机器人

自然语言处理

计算机视觉

金融和商业管理

更多应用

讨论

---

1. Silver, D. (2015). UCL reinforcement learning course. http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html. ↩︎

2. Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learning: An Introduction (2nd Edition). MIT Press. ↩︎