各种排序算法的详细比较(C++)，冒泡、插入、希尔、选择、堆排序、归并(递归)、归并(非递归)

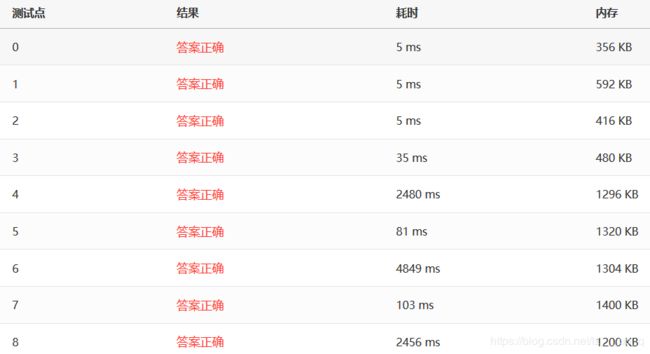
1 下面依次放各种算法对不同测试数据的运行时间

冒泡排序：

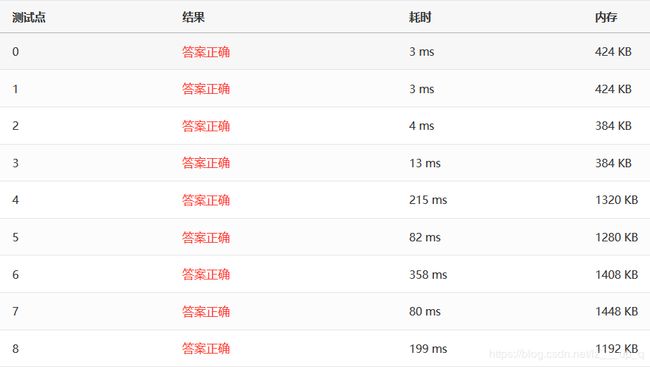
插入排序：

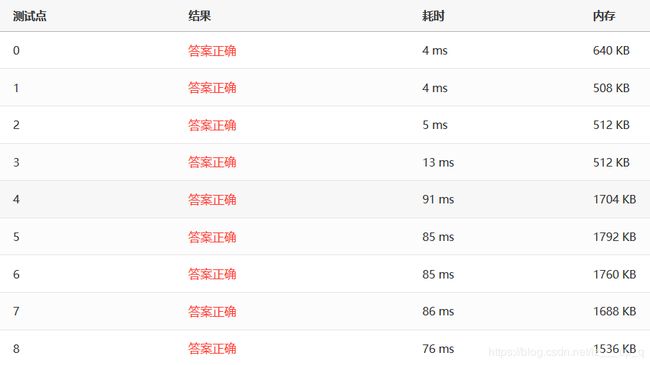
选择排序：

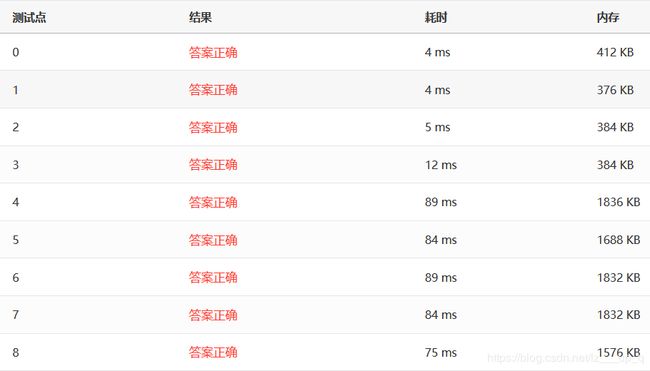
希尔排序—Sedgewick序列(4个点)

堆排序

归并排序（递归方式）

归并排序（非递归方式）

希尔排序—Sedgewick序列(15个点)

2 运行速度

可以看出，运行速度上希尔排序（Sedgewick15个点）>>归并（非递归）>=归并（递归）>=堆排序>希尔排序（Sedgewick4个点）>>插入>>选择>>冒泡

其中归并（递归）和归并（非递归）很接近，不知道是不是代码编译时，递归被优化过的缘故

希尔排序（Sedgewick15个点），归并（递归）和归并（非递归）以及堆排序四者也比较接近，但对于数据6和数据8（顺序整数和基本有序的整数），希尔（无论是4个点还是15个点）的表现非常好比另外三个都要快

另外对于同为O(n2)的冒泡、选择、插入，其中插入最快，选择次之，冒泡数据量过大会超时，其中选择排序对于数据6和数据8(顺序整数和基本有序的整数)也很快

3 时间复杂度的分析：

对于希尔排序，它是插入的改进版，若采用不同的序列，其时间复杂度也不一样

对于堆排序，它是选择排序的改进版，时间复杂度接近O(nlogn),其实比O(nlogn)还要小一点

 

对于归并排序，其时间复杂度为O(nlogn),最坏情况下也是nlogn，但其最大的缺点是需要一个额外的空间当临时数组

4 下面讨论稳定性

对于稳定性：冒泡、插入、归并都是稳定的

其他不稳定

5 最后附上完整的代码

#include
#include
using namespace std;

void Swap(int& a, int& b);
void BuildHeap(int A[], int last);
void PercDown(int A[], int m, int last);
void Msort(int A[], int temA[], int L, int RightEnd);
void Merge(int A[], int temA[], int L, int R, int RightEnd);
void Merge_Pass(int A[], int temA[], int N, int length);
void Merge1(int A[], int temA[], int L, int R, int RightEnd);
int MinPostion(int A[], int left, int right);
void Bubble_Sort(int A[], int N);//冒泡排序
void Insertion_Sort(int A[], int N);//插入排序
void Shell_Sort(int A[], int N);//希尔排序
void Selection_Sort(int A[], int N);//选择排序
void Heap_Sort(int A[], int N);//堆排序
void Merge_Sort(int A[], int N);//归并排序
void Merge_Sort_None_recursive(int A[], int N);//归并排序_非递归

int main() {
	int N;
	int* A = NULL;
	cin >> N;
	A = new int[N]();
	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}
	//各种排序算法,升序
	//Bubble_Sort(A,N);
	//Insertion_Sort(A, N);
	Shell_Sort(A, N);
	//Selection_Sort(A, N);
	//Heap_Sort(A, N);
	//Merge_Sort(A, N);
	//Merge_Sort_None_recursive(A,N);
	//输出
	for (int i = 0; i < N; i++) {
		cout << A[i];
		if (i < N - 1) {
			cout << " ";
		}
	}
	//cout << "The run time is:" << (double)clock() / CLOCKS_PER_SEC << "s" << endl;
	return 0;
}
void Merge_Sort_None_recursive(int A[], int N) {
	int *temA = NULL;
	int length;
	temA = new int[N]();
	for (length = 1; length < N; ) {
		Merge_Pass(A, temA,N,length);
		length = length * 2;
		Merge_Pass(temA, A, N, length);
		length = length * 2;
	}
}
void Merge_Pass(int A[], int temA[], int N, int length) {
	int i;
	for (i = 0; i + 2 * length - 1 < N; i = i + 2 * length) {
		Merge1(A, temA, i, i + length, i + 2 * length - 1);
	}
	if (i + length < N) {    //说明存在两个子列
		Merge1(A, temA, i, i + length, N - 1);
	}
	else {                   //说明只有一个子列，直接转移到temA中
		for (; i < N; i++) {
			temA[i] = A[i];
		}
	}
}
void Merge1(int A[], int temA[], int L, int R, int RightEnd) {//合并后的数组放在temA中
	int LeftEnd = R - 1;
	int temPoint = L;
	int p = L;//因为L会变，所以先把它保留下来
	for (; L <= LeftEnd && R <= RightEnd;) {
		if (A[L] > A[R]) temA[temPoint++] = A[R++];
		else temA[temPoint++] = A[L++];
	}
	while (L <= LeftEnd) {
		temA[temPoint++] = A[L++];
	}
	while (R <= RightEnd) {
		temA[temPoint++] = A[R++];
	}
}
void Merge_Sort(int A[], int N) {
	int* temA = NULL;
	temA = new int[N]();
	Msort(A,temA,0,N-1);
}
void Msort(int A[],int temA[],int L,int RightEnd) {
	int center;
	if (L < RightEnd) {
		center = (L + RightEnd) / 2;
		Msort(A, temA, L, center);
		Msort(A, temA, center + 1, RightEnd);
		Merge(A, temA, L, center + 1, RightEnd);
	}
}
void Merge(int A[], int temA[], int L, int R, int RightEnd) {
	int LeftEnd = R - 1;
	int temPoint=L;
	int p = L;//因为L会变，所以先把它保留下来
	for (; L <= LeftEnd && R <= RightEnd;) {
		if (A[L] > A[R]) temA[temPoint++] = A[R++];
		else temA[temPoint++] = A[L++];
	}
	while (L <= LeftEnd) {
		temA[temPoint++] = A[L++];
	}
	while (R <= RightEnd) {
		temA[temPoint++] = A[R++];
	}
	for (int i =p; i<=RightEnd; i++) {
		A[i] = temA[i];
	}
}
void Heap_Sort(int A[], int N) {
	BuildHeap(A, N - 1);
	Swap(A[0], A[N-1]);
	for (int i = N -2; i > 0; i--) {
		PercDown(A, 0, i);
		Swap(A[0], A[i]);
	}
}
void PercDown(int A[],int m,int last) {//调整第m个元素，数组的最后一个元素位置为last
	int temp;
	int parent, child;
	parent = m;
	temp = A[parent];
	for (; 2 * parent + 1 <= last;) {
		child = 2 * parent + 1;
		if (childA[child]) {
			child++;
		}
		if (temp > A[child]) break;
		else {
			A[parent] = A[child];
			parent = child;
		}
	}
	A[parent] = temp;
}
void BuildHeap(int A[],int last) { //堆和堆的最后一个元素的位置,这里的堆从零开始计数
	int i;
	for (i = (last - 1) / 2; i >= 0; i--) {
		PercDown(A, i, last);
	}

}
void Selection_Sort(int A[], int N) {
	for (int i = 0; i < N; i++) {
		Swap(A[i],A[MinPostion(A, i,N)]);
	}
}
int MinPostion(int A[], int left, int right) {
	int minv = left;
	for (int i = left; i < right; i++) {
		if (A[i] < A[minv]) { 
			minv =i; 
		}
	}
	return minv;
}
void Shell_Sort(int A[], int N) {
	int Sedgewick[] = { 1 ,5 ,19 ,41 ,109 ,209, 505, 929, 2161, 3905, 8929, 16001, 36289, 64769, 146305 };
	int D;
	int temp;
	int i,j,P;
	for (j = 14; j >= 0; j--) {
		D = Sedgewick[j];
		for (P = D; P < N;P++) {
			temp = A[P];
			for (i = P; i - D >= 0 && A[i - D] > temp;i=i-D) {
				A[i] = A[i-D];
			}
			A[i] = temp;
		}
	}
}
void Insertion_Sort(int A[], int N) {
	int temp, i;
	for (int k = 1; k < N; k++) {
		temp = A[k];
		for (i = k; A[i - 1] > temp && i - 1 >= 0; i--) {
			A[i] = A[i - 1];
		}
		A[i] = temp;
	}
}
void Bubble_Sort(int A[], int N) {
	for (int p = N; p > 1; p--) {
		for (int i = 0; i < p - 1; i++) {
			if (A[i] > A[i + 1]) {
				Swap(A[i], A[i + 1]);
			}
		}
	}
}
void Swap(int& a, int& b) {
	int temp;
	temp = a;
	a = b;
	b = temp;
}