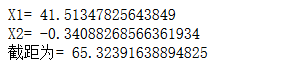人工智能与机器学习——梯度下降法求函数极值

一、原理介绍

1. 梯度下降法的原理

梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。

2. 梯度下降法求解过程

顾名思义，梯度下降法的计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）。

其迭代公式为, 其中代表梯度负方向，
表示梯度方向上的搜索步长。梯度方向我们可以通过对函数求导得到，步长的确定比较麻烦，太大了的话可能会发散，太小收敛速度又太慢。一般确定步长的方法是由线性搜索算法来确定，即把下一个点的坐标看做是ak+1的函数，然后求满足f(ak+1)的最小值的ak+1即可。

因为一般情况下，梯度向量为0的话说明是到了一个极值点，此时梯度的幅值也为0.而采用梯度下降算法进行最优化求解时，算法迭代的终止条件是梯度向量的幅值接近0即可，可以设置个非常小的常数阈值。

3. 牛顿法原理

牛顿法（英语：Newton’s method）又称为牛顿-拉弗森方法（英语：Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数的泰勒级数的前面几项来寻找方程的根。

4. 牛顿法方法说明

二、用Excel完成函数极值的求解

1. 求解函数题目

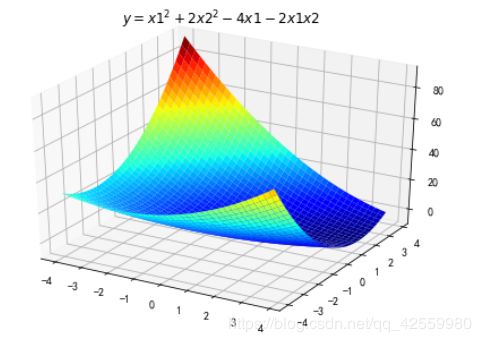
用梯度法求二次函数的极小点及极小值，函数如下：
已知初始点,迭代精度

2. 用excel计算

① ∂z/∂x1 计算方法

② ∂z/∂x2 计算方法

③ ⊿x1 计算方法

η*∂z/∂x1

④ ⊿x2 计算方法

η*∂z/∂x2

3. 计算结果

极小点（4,2） 极小值-8

三、用 Python编程完成函数极值的求解

1. 显示函数图像

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings
 
# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
%matplotlib inline
 

"""
二维原始图像
1、构建一个函数为 y = x1^2 + 2 x2^2 - 4 x1 - 2 x1 x2 的图像。
2、随机生成X1,X2点，根据X1,X2点生成Y点。
3、画出图像。
"""
def f2(x1,x2):
    return x1**2 + 2 * x2**2 - 4*x1 - 2 * x1 * x2 
 
X1 = np.arange(-4,4,0.2)
X2 = np.arange(-4,4,0.2)
X1, X2 = np.meshgrid(X1, X2) # 生成xv、yv，将X1、X2变成n*m的矩阵，方便后面绘图
Y = np.array(list(map(lambda t : f2(t[0],t[1]),zip(X1.flatten(),X2.flatten()))))
Y.shape = X1.shape # 1600的Y图还原成原来的（40,40）
 
%matplotlib inline
#作图
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.set_title(u'$ y = x1^2 + 2 x2^2 - 4 x1 - 2 x1 x2 $')
plt.show()

运行结果：

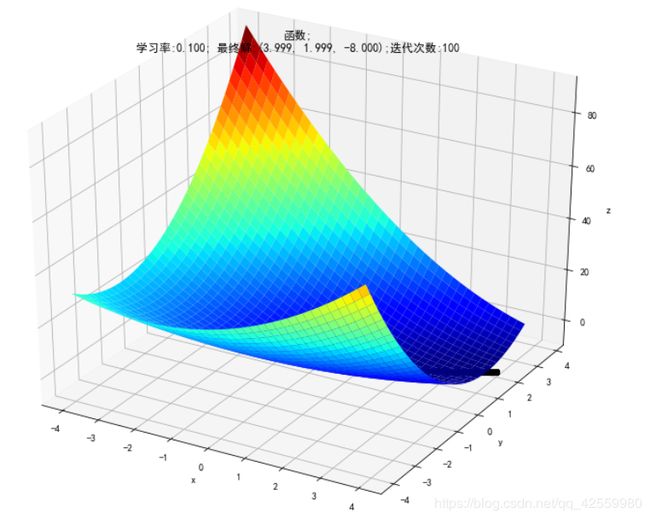
2. 求函数极值

"""
对当前二维图像求最小点¶
1、随机取一个点（x1,x2）,设定α参数值  
2、对这个点分别求关于x1、x2的偏导数，x1 =x1 - α*(dY/dx1),x2 =x2 - α*(dY/dx2)  
3、重复第二补，设置 y的变化量 小于多少时 不再重复。
"""
# 二维原始图像
def f2(x, y):
    return x**2+2*(y)**2 - 4*(x)-2*(x)*(y)  
## 偏函数
def hx1(x, y):
    return 2*x-4-2*y
def hx2(x, y):
    return 4*y-2*x

X1 = np.arange(-4,4,0.2)
X2 = np.arange(-4,4,0.2)

X1, X2 = np.meshgrid(X1, X2) # 生成xv、yv，将X1、X2变成n*m的矩阵，方便后面绘图
Y = np.array(list(map(lambda t : f2(t[0],t[1]),zip(X1.flatten(),X2.flatten()))))
Y.shape = X1.shape # 1600的Y图还原成原来的（40,40）


x1 = 1
x2 = 1
alpha = 0.1
#保存梯度下降经过的点
GD_X1 = [x1]
GD_X2 = [x2]
GD_Y = [f2(x1,x2)]
# 定义y的变化量和迭代次数
y_change = f2(x1,x2)
iter_num = 0
 
while(y_change < 1e-10 and iter_num < 100) :
    tmp_x1 = x1 - alpha * hx1(x1,x2)
    tmp_x2 = x2 - alpha * hx2(x1,x2)
    tmp_y = f2(tmp_x1,tmp_x2)
    
    f_change = np.absolute(tmp_y - f2(x1,x2))
    x1 = tmp_x1
    x2 = tmp_x2
    GD_X1.append(x1)
    GD_X2.append(x2)
    GD_Y.append(tmp_y)
    iter_num += 1
print(u"最终结果为:(%.5f, %.5f, %.5f)" % (x1, x2, f2(x1,x2)))
print(u"迭代过程中X的取值，迭代次数:%d" % iter_num)
print(GD_X1)
 
# 作图
fig = plt.figure(facecolor='w',figsize=(6,4))
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(GD_X1,GD_X2,GD_Y,'ko-')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title(u'$ y = x1^2+2(x2)^2 - 4(x1)-2(x1) (x2) $')
 
ax.set_title(u'函数;\n学习率:%.3f; 最终解:(%.3f, %.3f, %.3f);迭代次数:%d' % (alpha, x1, x2, f2(x1,x2), iter_num))
plt.show()

运行结果：

四、梯度下降法求店铺面积与营业额问题

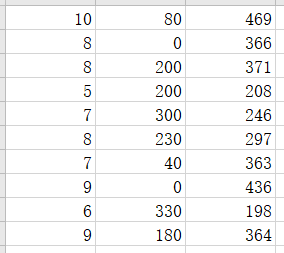
1. excel表格

2. python代码

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
%matplotlib inline

data=np.genfromtxt('E:\面积距离车站数据.csv',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,2]
#定义学习率、斜率、截据
#设方程为y=theta1x1+theta2x2+theta0
lr=0.00001
theta0=0
theta1=0
theta2=0
#定义最大迭代次数，因为梯度下降法是在不断迭代更新k与b
epochs=10000
#定义最小二乘法函数-损失函数（代价函数）
def compute_error(theta0,theta1,theta2,x_data,y_data):
    totalerror=0
    for i in range(0,len(x_data)):#定义一共有多少样本点
        totalerror=totalerror+(y_data[i]-(theta1*x_data[i,0]+theta2*x_data[i,1]+theta0))**2
    return totalerror/float(len(x_data))/2
#梯度下降算法求解参数
def gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs):
    m=len(x_data)
    for i in range(epochs):
        theta0_grad=0
        theta1_grad=0
        theta2_grad=0
        for j in range(0,m):
            theta0_grad-=(1/m)*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta2)+y_data[j])
            theta1_grad-=(1/m)*x_data[j,0]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
            theta2_grad-=(1/m)*x_data[j,1]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
        theta0=theta0-lr*theta0_grad
        theta1=theta1-lr*theta1_grad
        theta2=theta2-lr*theta2_grad
    return theta0,theta1,theta2
#进行迭代求解
theta0,theta1,theta2=gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs)
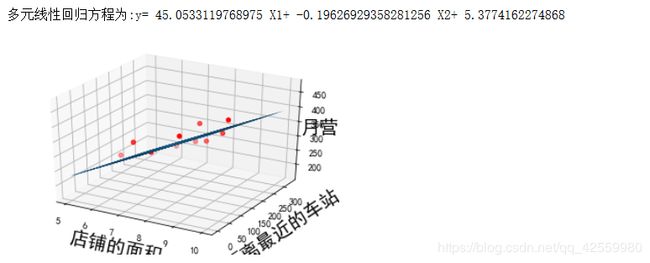
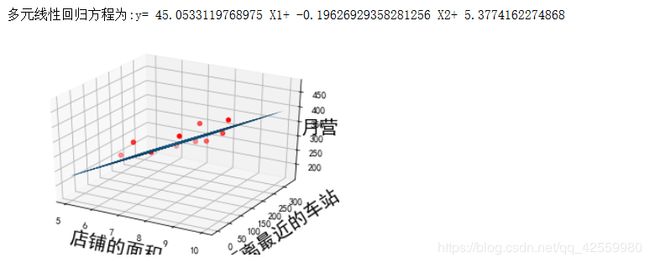
print("多元线性回归方程为:y=",theta1,"X1+",theta2,"X2+",theta0)
ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o')
x0=x_data[:,0]
x1=x_data[:,1]
#生成网格矩阵
x0,x1=np.meshgrid(x0,x1)
z=theta0+theta1*x0+theta2*x1
#画3d图
ax.plot_surface(x0,x1,z)
ax.set_xlabel('店铺的面积',fontsize=20)
ax.set_ylabel('距离最近的车站',fontsize=20)
ax.set_zlabel("月营业额",fontsize=20)
plt.show()

3. 运行结果

五、最小二乘法求店铺面积与营业额问题

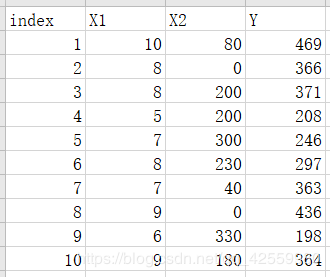
1. excel表格

2. 求解二元线性回归方程

from sklearn import linear_model        #表示，可以调用sklearn中的linear_model模块进行线性回归。
import pandas as pd
import seaborn as sns  
import matplotlib.pyplot as plt
%matplotlib inline

data=pd.read_excel('E:\营业额数据.xlsx')

X=data[['X1','X2']]   
y=data['Y']    
y=data.Y   

model = linear_model.LinearRegression()
model.fit(X,y)  

print("X1=",model.coef_[0])
print("X2=",model.coef_[1])
print("截距为=",model.intercept_)

print("多元线性回归方程为:y=",model.coef_[0],"X1",model.coef_[1],"X2+",model.intercept_)

sns.pairplot(data, x_vars=['X1','X2'], y_vars='Y', height=3, aspect=0.8, kind='reg')  
plt.show()  

六、比较最小二乘法和梯度下降法

1. 梯度下降法

2. 最小二乘法

七、参考文献

① 《梯度下降》.天眼侍者.搜狗百科.2019-01-18
链接: 梯度下降.

② 《牛顿法》.≈风过无痕≈.搜狗百科.2018-10-25
链接: 牛顿法.