Doing Math with Python读书笔记-第2章：Visualizing Data with Graphs

本章我们会使用绘图包matplotlib，因此先安装：

$ pip3 install --user matplotlib 
WARNING: pip is being invoked by an old script wrapper. This will fail in a future version of pip.
Please see https://github.com/pypa/pip/issues/5599 for advice on fixing the underlying issue.
To avoid this problem you can invoke Python with '-m pip' instead of running pip directly.
Collecting matplotlib
  Downloading matplotlib-3.1.3-cp38-cp38-manylinux1_x86_64.whl (13.1 MB)
     |████████████████████████████████| 13.1 MB 4.5 kB/s 
Collecting numpy>=1.11
  Downloading numpy-1.18.1-cp38-cp38-manylinux1_x86_64.whl (20.6 MB)
     |████████████████████████████████| 20.6 MB 12 kB/s 
Collecting pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.1
  Using cached pyparsing-2.4.6-py2.py3-none-any.whl (67 kB)
Collecting cycler>=0.10
  Using cached cycler-0.10.0-py2.py3-none-any.whl (6.5 kB)
Collecting kiwisolver>=1.0.1
  Downloading kiwisolver-1.1.0-cp38-cp38-manylinux1_x86_64.whl (91 kB)
     |████████████████████████████████| 91 kB 10 kB/s 
Collecting python-dateutil>=2.1
  Using cached python_dateutil-2.8.1-py2.py3-none-any.whl (227 kB)
Requirement already satisfied: six in /home/xiaoyu/.local/lib/python3.8/site-packages (from cycler>=0.10->matplotlib) (1.14.0)
Requirement already satisfied: setuptools in /usr/local/lib/python3.8/site-packages (from kiwisolver>=1.0.1->matplotlib) (41.2.0)
Installing collected packages: numpy, pyparsing, cycler, kiwisolver, python-dateutil, matplotlib
Successfully installed cycler-0.10.0 kiwisolver-1.1.0 matplotlib-3.1.3 numpy-1.18.1 pyparsing-2.4.6 python-dateutil-2.8.1

了解笛卡尔坐标平面

横轴x，纵轴y。坐标(x,y)，原点为(0,0)

LIST 和 TUPLE

list和tuple是存储一组值(不仅仅是数值)的两种方法。区别是list可以修改，tuple不行。
因此如果你一开始就可以确定这些数值，就用tuple，否则用list。
使用这两种方法的好处是不必为每一个数值赋予变量名，只需要用数字索引就可以引用它们。

>>> list1 = [1, 2, 3, 4]
>>> list1[0]
1
>>> tuple1 = (1, 2, 3, 4)
>>> tuple1[0]
1

list后续可以增删成员：

>>> emptylist = []
>>> emptylist.append(1)
>>> emptylist.append(2)
>>> emptylist
[1, 2]
>>> del(emptylist[0])
>>> emptylist
[2]

索引可以为负数，表示倒数：

>>> list1[-1]
4
>>> list1[-2]
3

遍历

>>> for i in list1:
...     print(i)
... 
1
2
3
4

enumerate在遍历的同时可以返回索引值：

>>> for idx, n in enumerate(list1):
...     print(idx, n)
... 
0 1
1 2
2 3
3 4

用MATPLOTLIB绘图

matplotlib是一个package，包含很多module。

>>> x = [1, 2, 3]
>>> y = [2, 4, 6]
>>> from pylab import plot, show	# pylab是matplotlib的一部分
>>> plot(x, y)
[<matplotlib.lines.Line2D object at 0x7fb5d6d378b0>]
>>> show()	# 显示图形，程序阻塞直到你关闭图形。

从图形中可看到，左下角的坐标并非(0, 0)，而是两个list中的最小值(1, 2)，而右上角则是两个list中的最大值(3, 6)

画点

>>> plot(x, y, marker='o')	# 标记可以是'o', '*', 'x', 和 '+'。
>>> show()	# 三个点会用'o'标记，并被连接

>>> plot(x, y, 'o')
>>> show()	# 仅显示三个点，没有线连接

绘制纽约年度平均温度
2000-2012年，每年一个值。

>>> nyc_temp = [53.9, 56.3, 56.4, 53.4, 54.5, 55.8, 56.8, 55.0, 55.3, 54.0, 56.7, 56.4, 57.3]
>>> plot(nyc_temp, marker='o')	# 由于x轴可以不指定，因此这里的nyc_temp表示y轴
# 如果希望上面的点表示x轴，可以plot(nyc_temp, [0]*13, marker='o')
>>> show()

上图有几点注意，这些都可以调整：

• 温差不大，但图形显示差距很大，这是由于y轴的最小和最大值和温度数据关联
• x轴整数，y轴是浮点数

将横坐标设置为年度：

>>> years = range(2000, 2013)
>>> plot(years, nyc_temp, marker='o')
[<matplotlib.lines.Line2D object at 0x7fb5d6468a30>]
>>> show()

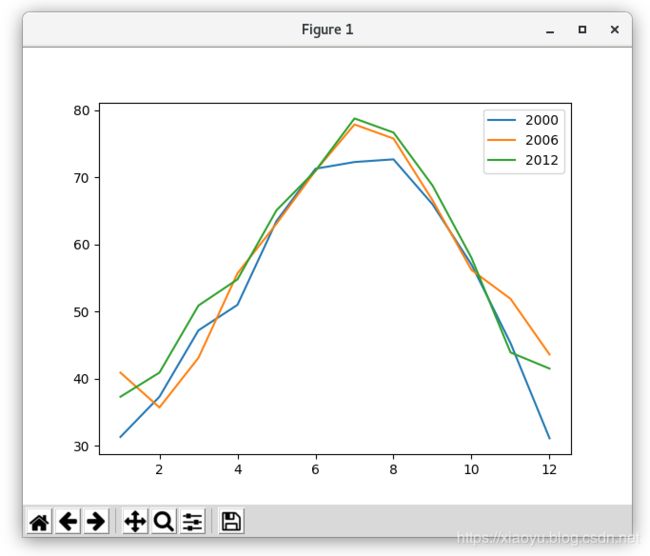
比较纽约的月度温度趋势
选取了3年，每年12个月。运行以下代码：

nyc_temp_2000 = [31.3, 37.3, 47.2, 51.0, 63.5, 71.3, 72.3, 72.7, 66.0, 57.0, 45.3, 31.1]
nyc_temp_2006 = [40.9, 35.7, 43.1, 55.7, 63.1, 71.0, 77.9, 75.8, 66.6, 56.2, 51.9, 43.6]
nyc_temp_2012 = [37.3, 40.9, 50.9, 54.8, 65.1, 71.0, 78.8, 76.7, 68.8, 58.0, 43.9, 41.5]
months = range(1, 13)
# 以下的plot等同于plot(months, nyc_temp_2000)加上plot(months, nyc_temp_2006), 加上plot(months, nyc_temp_2012)，一次性返回3个matplotlib.lines.Line2D对象
plot(months, nyc_temp_2000, months, nyc_temp_2006, months, nyc_temp_2012)
from pylab import legend	# 用于加图例，可选。默认位置在右上，可设置。
legend([2000, 2006, 2012])	# 顺序和3个plot对象对应

定制图表
前面谈到的加图例是定制的一种。
加标题和标签

>>> from pylab import plot, show, title, xlabel, ylabel, legend
>>> title('Average monthly temperature in NYC')
Text(0.5, 1.0, 'Average monthly temperature in NYC')
>>> xlabel('Month')
Text(0.5, 0, 'Month')
>>> ylabel('Temperature')
Text(0, 0.5, 'Temperature')

定制坐标轴
回顾之前纽约年度平均气温的例子，温度相差不大，但图形显示上差别很大。这可以通过设置横纵坐标的起始值调整：

>>> from pylab import plot, show
>>> nyc_temp = [53.9, 56.3, 56.4, 53.4, 54.5, 55.8, 56.8, 55.0, 55.3, 54.0, 56.7, 56.4, 57.3]
>>> plot(nyc_temp, marker='o')
[<matplotlib.lines.Line2D object at 0x7fe691f5fa60>]
>>> from pylab import axis
>>> axis()	返回的tuple为(xmin, xmax, ymin, ymax)
(-0.6000000000000001, 12.6, 53.205, 57.495)
>>> axis(ymin=0)
(-0.6000000000000001, 12.6, 0, 57.495)

使用pyplot绘图
以上我们都是用pylab绘图，这在IDLE或交互式shell中是合适的，但对于大型程序，建议用pyplot。
用户和pylab类似，例如：

import matplotlib.pyplot	# 引入整个pyplot模块
x_numbers = [1, 2, 3]
y_numbers = [2, 4, 6]
matplotlib.pyplot.plot(x_numbers, y_numbers)
matplotlib.pyplot.show()

简介的写法可以为引入的模块加别名，例如：

import matplotlib.pyplot as plt
...
plt.plot(x_numbers, y_numbers)
plt.show()

保存绘图
在显示的图表上有保存按钮。
无论是pylab还是pyplot，都可以用savefig(filename)，可以保存为PDF，PNG和SVG格式。

通过公式绘图

牛顿万有引力定律（Newton’s Law of Universal Gravitation）
如下，$m_1$和$m_1$表示两个物体的质量，r表示两个物体的距离，G是重力常数：
$F=\frac{G{m}_1{m}_2}{r^2}$
这里假定$m_1$和$m_1$分布为0.5和1.5公斤，需绘制F和r的关系。
代码如下：

import matplotlib.pyplot as plt
m1 = 0.5; m2 = 1.5; G = 6.674*(10**-11)
r = range(100, 1001, 50)
F = []
for dist in r:
	force = G*(m1*m2)/(dist**2)
	F.append(force)

plt.plot(r, F, marker='o')
plt.xlabel('Distance in meters')
plt.ylabel('Gravitational force in newtons')
plt.title('Gravitational force and distance')
plt.show()

输出如下：

抛体运动（Projectile Motion）
若初始速度为$\mu$，投射角度为$\theta$，则：
${\mu }_x=\mu \ast cos\theta$
${\mu }_y=\mu \ast sin\theta$
公式的推演暂不赘述。Latex数学公式的语法见这里。

这一段程序需要了解的几点。

1. 模拟range()编写了frange()函数提供浮点数的列表
2. 利用了math库中radians()和sin()和cos()函数

以下复习下数学。
radians是将角度转换为弧度，记住$2\pi =360^0$就好。

>>> import math
>>> math.radians(45)
0.7853981633974483
>>> math.radians(180)
3.141592653589793

cos和sin的原理：

三角函数表见这里：

>>> math.cos(math.radians(90))
6.123233995736766e-17
>>> math.sin(math.radians(90))
1.0
>>> math.sin(math.radians(45))
0.7071067811865475
>>> 2**(1/2)/2
0.7071067811865476
>>> math.cos(0)
1.0

编程挑战

条形图
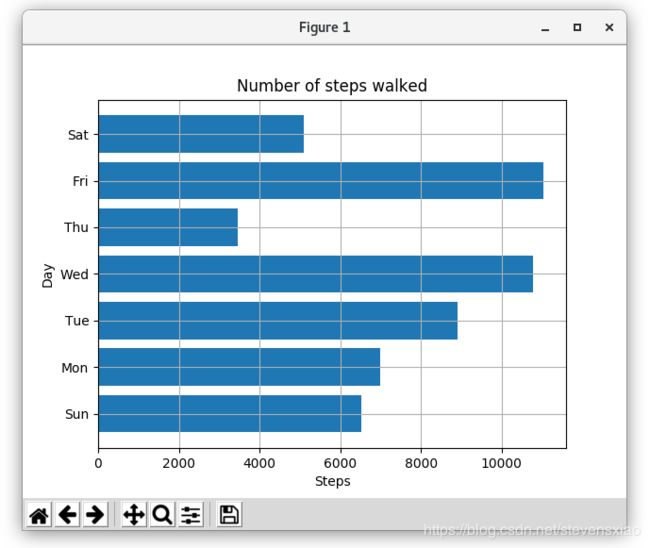
这一部分讲述了如何使用pyplot.barh()做条形图(Bar Chart):

>>> import matplotlib.pyplot as plt
>>> labels = ['Sun', 'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat']
>>> steps = [6534, 7000, 8900, 10786, 3467, 11045, 5095]
>>> positions = range(1, len(steps)+1)
>>> plt.barh(positions, steps, align='center')
<BarContainer object of 7 artists>
>>> plt.yticks(positions, labels)
([<matplotlib.axis.YTick object at 0x7f43a1c14c70>, <matplotlib.axis.YTick object at 0x7f43a1c14850>, <matplotlib.axis.YTick object at 0x7f43a48c4f70>, <matplotlib.axis.YTick object at 0x7f43a1bf10a0>, <matplotlib.axis.YTick object at 0x7f43a1bf1640>, <matplotlib.axis.YTick object at 0x7f43a1bf1be0>, <matplotlib.axis.YTick object at 0x7f43a1bf61c0>], <a list of 7 Text yticklabel objects>)
>>> plt.xlabel('Steps')
Text(0.5, 0, 'Steps')
>>> plt.ylabel('Day')
Text(0, 0.5, 'Day')
>>> plt.title('Number of steps walked')
Text(0.5, 1.0, 'Number of steps walked')
>>> plt.grid()
>>> plt.show()

输出为：

Fibonacci序列黄金比例
我实现的代码如下：

def fibo(n):
    f = [1, 2]
    if n <= 2:
        return f[:n]

    for i in range(2, n):
        f.append(f[i-2] + f[i-1])

    return f

def gold_ratio(f):
    r = []
    size = len(f)
    if size >= 2:
        for i in range(2, size + 1):
            r.append(f[i-1]/f[i-2])

    return r


import matplotlib.pyplot as plt
items=50
plt.title('Golden Ratio for Fibonacci Sequence')
plt.xlabel('n')
plt.ylabel('ratio')
plt.plot(gold_ratio(fibo(items)))
plt.show()

输出如下，当n增加时，比例趋近黄金比例1.618：