线性分类的数学基础与应用、Fisher判别的推导（python）、Fisher分类器（线性判别分析，LDA）

一、线性分类的数学基础与应用

1、Fisher基本介绍

Fisher判别法是一种投影方法，把高维空间的点向低维空间投影。在原来的坐标系下，可能很难把样品分开，而投影后可能区别明显。一般说，可以先投影到一维空间(直线)上，如果效果不理想，在投影到另一条直线上(从而构成二维空间)，依此类推，每个投影可以建立一个判别函数。

2、Fisher判别思想

①以二维模式样本为例

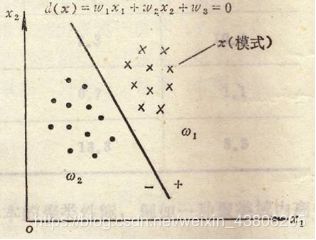
②用判别函数进行模式分类依赖的两个因素
a.判别函数的几何性质：线性的和非线性的函数。 线性的是一条直线； 非线性的可以是曲线、折线等； 线性判别函数建立起来比较简单（实际应用较多）； 非线性判别函数建立起来比较复杂。
b. 判别函数的系数：判别函数的形式确定后，主要就是确定判别函数的系数问题。 只要被研究的模式是可分的，就能用给定的模式样本集来确定判别函数的系数。

③n维线性判别函数的一般形式
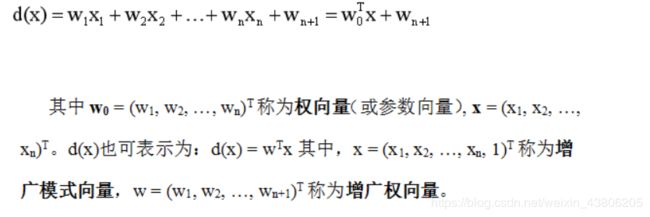④两类情况：判别函数d(x)
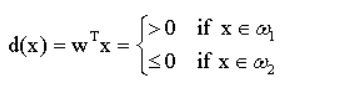⑤多类情况
设模式可分成ω1, ω2,…, ωM共M类，则有三种划分方法

3、举例

①例题
②手工推导

二、Fisher判别的推导（python）

1、代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt 
import seaborn as sns
path=r'C:/Users/LOL/Desktop/Iris.csv'
df = pd.read_csv(path, header=0)
Iris1=df.values[0:50,0:4]
Iris2=df.values[50:100,0:4]
Iris3=df.values[100:150,0:4]

#类均值向量
m1=np.mean(Iris1,axis=0)
m2=np.mean(Iris2,axis=0)
m3=np.mean(Iris3,axis=0)

#各类内离散度矩阵
s1=np.zeros((4,4))
s2=np.zeros((4,4))
s3=np.zeros((4,4))
for i in range(0,30,1):
    a=Iris1[i,:]-m1
    a=np.array([a])
    b=a.T
    s1=s1+np.dot(b,a)    
for i in range(0,30,1):
    c=Iris2[i,:]-m2
    c=np.array([c])
    d=c.T
    s2=s2+np.dot(d,c) 
for i in range(0,30,1):
    a=Iris3[i,:]-m3
    a=np.array([a])
    b=a.T
    s3=s3+np.dot(b,a) 

#总类内离散矩阵
sw12=s1+s2
sw13=s1+s3
sw23=s2+s3
#投影方向
a=np.array([m1-m2])
sw12=np.array(sw12,dtype='float')
sw13=np.array(sw13,dtype='float')
sw23=np.array(sw23,dtype='float')
#判别函数以及T
#需要先将m1-m2转化成矩阵才能进行求其转置矩阵
a=m1-m2
a=np.array([a])
a=a.T
b=m1-m3
b=np.array([b])
b=b.T
c=m2-m3
c=np.array([c])
c=c.T
w12=(np.dot(np.linalg.inv(sw12),a)).T
w13=(np.dot(np.linalg.inv(sw13),b)).T
w23=(np.dot(np.linalg.inv(sw23),c)).T
#print(m1+m2) #1x4维度  invsw12 4x4维度  m1-m2 4x1维度
#判别函数以及阈值T（即w0）
T12=-0.5*(np.dot(np.dot((m1+m2),np.linalg.inv(sw12)),a))
T13=-0.5*(np.dot(np.dot((m1+m3),np.linalg.inv(sw13)),b))
T23=-0.5*(np.dot(np.dot((m2+m3),np.linalg.inv(sw23)),c))
kind1=0
kind2=0
kind3=0
newiris1=[]
newiris2=[]
newiris3=[]
for i in range(30,49):
    x=Iris1[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
        kind1=kind1+1
    elif g12<0 and g23>0:
        newiris2.extend(x)
    elif g13<0 and g23<0 :
        newiris3.extend(x)
#print(newiris1)
for i in range(30,49):
    x=Iris2[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
    elif g12<0 and g23>0:
 
        newiris2.extend(x)
        kind2=kind2+1
    elif g13<0 and g23<0 :
        newiris3.extend(x)
for i in range(30,49):
    x=Iris3[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
    elif g12<0 and g23>0:     
        newiris2.extend(x)
    elif g13<0 and g23<0 :
        newiris3.extend(x)
        kind3=kind3+1
correct=(kind1+kind2+kind3)/60
print("样本类内离散度矩阵S1：",s1,'\n')
print("样本类内离散度矩阵S2：",s2,'\n')
print("样本类内离散度矩阵S3：",s3,'\n')
print("总体类内离散度矩阵Sw12：",sw12,'\n')
print("总体类内离散度矩阵Sw13：",sw13,'\n')
print("总体类内离散度矩阵Sw23：",sw23,'\n')
print('判断出来的综合正确率：',correct*100,'%')

2、代码结果

三、Fisher分类器

1、定义

Fisher分类器也叫Fisher线性判别（Fisher Linear Discriminant），或称为线性判别分析（Linear Discriminant Analysis，LDA）。LDA有时也被称为Fisher’s LDA。最初于1936年，提出Fisher线性判别，后来于1948年，进行改进成如今所说的LDA。

2、scikit-learn中LDA的函数的代码测试

①代码

from sklearn import model_selection
from sklearn import datasets
from sklearn import discriminant_analysis
#用莺尾花数据集
def load_data():
    iris=datasets.load_iris()
    return model_selection.train_test_split(iris.data,iris.target,test_size=0.25,random_state=0,stratify=iris.target)  
    #返回为: 一个元组，依次为：训练样本集、测试样本集、训练样本的标记、测试样本的标记 
def test_LinearDiscriminantAnalysis(*data):
    x_train,x_test,y_train,y_test=data
    lda=discriminant_analysis.LinearDiscriminantAnalysis()
    lda.fit(x_train,y_train)
    print('Coefficients:%s, intercept %s'%(lda.coef_,lda.intercept_))#输出权重向量和b
    print('Score: %.2f' % lda.score(x_test, y_test))#测试集
    print('Score: %.2f' % lda.score(x_train, y_train))#训练集 
x_train,x_test,y_train,y_test=load_data()
test_LinearDiscriminantAnalysis(x_train,x_test,y_train,y_test)

②结果
由实验结果可知：在测试集上预测准确率为100%，而在训练集上预测准确率为97%

3、监督降维技术

该数据集是原始的数据集经过Fisher的投影
①代码

from sklearn import model_selection
from sklearn import datasets
from sklearn import discriminant_analysis
#用莺尾花数据集
def load_data():
    iris=datasets.load_iris()
    return model_selection.train_test_split(iris.data,iris.target,test_size=0.25,random_state=0,stratify=iris.target)  
    #返回为: 一个元组，依次为：训练样本集、测试样本集、训练样本的标记、测试样本的标记 
def plot_LDA(converted_X,y):
    '''
    绘制经过 LDA 转换后的数据
    :param converted_X: 经过 LDA转换后的样本集
    :param y: 样本集的标记
    :return:  None
    '''
    from mpl_toolkits.mplot3d import Axes3D
    import matplotlib.pyplot as plt 
    fig=plt.figure()
    ax=Axes3D(fig)
    colors='rgb'
    markers='o*s'
    for target,color,marker in zip([0,1,2],colors,markers):
        pos=(y==target).ravel()
        X=converted_X[pos,:]
        ax.scatter(X[:,0], X[:,1], X[:,2],color=color,marker=marker,
        label="Label %d"%target)
    ax.legend(loc="best")
    fig.suptitle("Iris After LDA")
    plt.show()
import numpy as np
x_train,x_test,y_train,y_test=load_data()
X=np.vstack((x_train,x_test))#沿着竖直方向将矩阵堆叠起来，把训练与测试的数据放一起来看
Y=np.vstack((y_train.reshape(y_train.size,1),y_test.reshape(y_test.size,1)))#沿着竖直方向将矩阵堆叠起来
lda = discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(X, Y)
converted_X=np.dot(X,np.transpose(lda.coef_))+lda.intercept_
plot_LDA(converted_X,Y)

②运行结果
由实验结果可以看出，Fisher确实能够实现降维。假设存在M个类，则多分类LDA可以将样本投影到M-1维空间。

四、参考文献

1、https://www.cnblogs.com/chihaoyuIsnotHere/p/9720457.html

2、https://blog.csdn.net/gwplovekimi/article/details/80299070?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1

3、http://bob0118.club/?p=266