线性规划Python实现：使用库函数和不使用库函数进行单纯形法（大M法）线性规划

单纯形法的原理

可以参考：线性规划之单纯形法【超详解+图解】.
大M法(big M method)是线性规划问题的约束条件(=)等式或（≥）大于型时，使用人工变量法后，寻找其初始基可行解的一种方法。
应用单纯形法在改进目标函数的过程中，如果原问题存在最优解，必然使人工变量逐步变为非基变量，或使其值为零。否则，目标函数值将不可能达到最小或最大。在迭代过程中，若全部人工变量变成非基变量，则可把人工变量所在的列从单纯形表中删去，此时便找到原问题的一个初始基可行解。若此基可行解不是原问题的最优解，则继续迭代，直至所有的检验数都小于等于0，求得最优解为止。（来源百度百科）
用单纯形法求解线性规划要先将线性规划变为标准形式，然后添加人工变量进行求解
max $2x_1+x_2+x_3$
$$s.t=\{\begin{array}{l}-2x_2\ge 2\\ \\ x_1-x_2+x_3=2\\ \\ x_2-x_3\le 1\\ \\ x_1,x_2,x_3\ge 0\end{array}$$
变为标准形式
max $2x_1+x_2+x_3+0x4+0x5$
$$s.t=\{\begin{array}{l}-2x_2-x4=2\\ \\ x_1-x_2+x_3=2\\ \\ x_2-x_3+x5=1\\ \\ x_1,x_2,x_3\ge 0\end{array}$$
加入人工变量：
max $2x_1+x_2+x_3+0x4+0x5-Mx6-Mx7$
$$s.t=\{\begin{array}{l}-2x_2-x4=2\\ \\ x_1-x_2+x_3+x5+x6=2\\ \\ x_2-x_3+x6+x7=1\\ \\ x_1,x_2,x_3\ge 0\end{array}$$
M是一个任意值的正数
根据上述方程组可以得到初始的基可行解，列出初始单纯形表

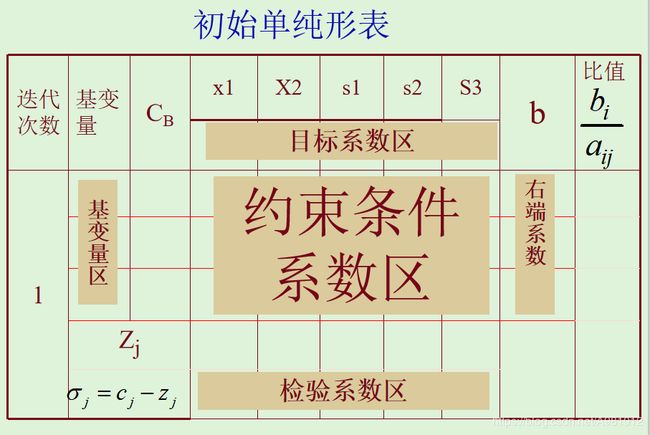
进行单纯形法迭代计算，根据检验数系数是否有正数，来判断是否要换基，然后又求检验数系数，判断是否换基，直到校验系数区没有正数时，若是基变量中含有非零的人工变量，则没有可行解，否则就有最优解

使用scipy库进行单纯形法线性规划

给出的线性规划为：max $2x_1+x_2+x_3$
$$s.t=\{\begin{array}{l}-2x_2\ge 2\\ \\ x_1-x_2+x_3=2\\ \\ x_2-x_3\le 1\\ \\ x_1,x_2,x_3\ge 0\end{array}$$

import numpy as np
from scipy.optimize import linprog 

a = np.array([2,1,1])#函数未知数的系数
A_ub = np.array([[0,2,-1],[0,1,-1]])#不等式约束变换为<=之后的系数
b_ub = np.array([-2,1])#为不等式约束的常数
A_eq = np.array([[1,-1,1]])#等式约束的系数
b_eq = np.array([2])#等式约束的常数
s = linprog(a,A_ub,b_ub,A_eq,b_eq,bounds=((0,None),(0,None),(0,None)))
print(s)

得到的结果：最优值为1.999999，$x_1=0,x_2=0,x_3=2$

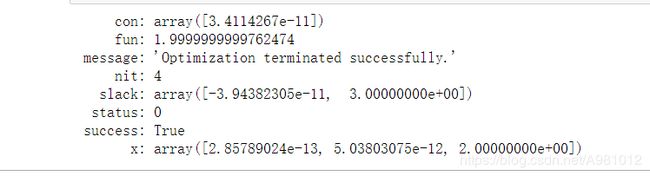
当然进行函数运行时，提前要检验是否有最优解。

不使用库函数进行单纯形法线

这个就比较难了就要先验证是否有最优解，然后才能通过程序进行运算。如果一个线性规划没有最优解，程序就会陷入死循环，不能得出运行结果。
给出的线性规划为：max $z=4x_1+3x_2$
$$s.t=\{\begin{array}{l}x1\le 6\\ \\ 2x2\le 8\\ \\ 2x1+3x2\le 18\\ \\ x1,x2\ge 0\\ \end{array}$$
加入松弛变量后
max $z=4x1+3x2+0x3+0x4+0x5$
$$s.t=\{\begin{array}{l}x1+x3=6\\ \\ 2x2+x4=8\\ \\ 2x1+3x2+x5=18\\ \\ x1,x2\ge 0\end{array}$$
根据约束条件和函数，可以看出函数是有最优解的：

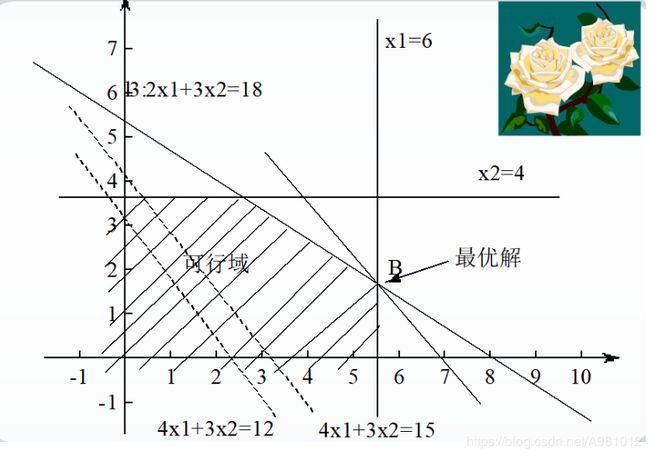
data.text中所存放的数据为

import numpy as np

def pivot():
    l = list(d[0][:-2])
    jnum = l.index(max(l)) #转入编号
    m = []
    for i in range(bn):
        if d[i][jnum] == 0:
            m.append(0.)
        else:
            m.append(d[i][-1]/d[i][jnum])
    inum = m.index(min([x for x in m[1:] if x!=0]))  #转出下标
    print("下标",inum)
    s[inum-1] = jnum
    r = d[inum][jnum]
    d[inum] /= r
    for i in [x for x in range(bn) if x !=inum]:
        r = d[i][jnum]
        d[i] -=r * d[inum]
        
def solve():
    flag = True
    while flag:
        if max(list(d[0][:-1])) <= 0: #直至所有系数小于等于0
            flag = False
        else:
            pivot()
            
def printSol():
    for i in range(cn - 1):
        if i in s:
            print("x"+str(i+1)+"=%.2f" % d[s.index(i)+1][-1])
        else:
            print("x"+str(i+1)+"=0.00")
    print("objective is %.2f"%(-d[0][-1]))
d = np.loadtxt("data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) #基变量列表
solve()
printSol()

结果显示为：

而对于最优解的线性规划：
给出的线性规划为：max $z=x_1+x_2$
$$s.t=\{\begin{array}{l}2x1-x2\ge 3\\ \\ x1-2x2\le 4\\ \\ x1+x2\ge 12\\ \\ x1,x2\ge 0\end{array}$$
加入松弛变量后：max $z=x_1+x_2+0x3+0x4$
$$s.t=\{\begin{array}{l}-2x1+x2+x3=3\\ \\ x1-2x2+x4=4\\ \\ x1+x2=12\\ \\ x1,x2,x3,x4\ge 0\end{array}$$
图中显示若是添加一个限制条件x1+x2>12，就不存在最优解

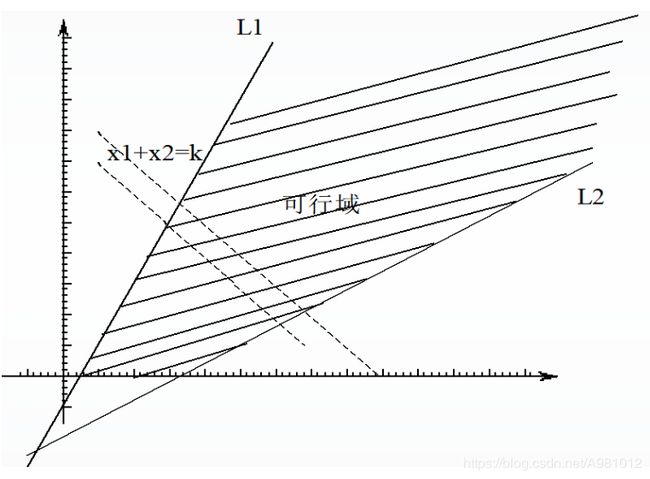
data1.text文件中的数据为：

程序运行的结果为：一直输出下标，说明一直在换基

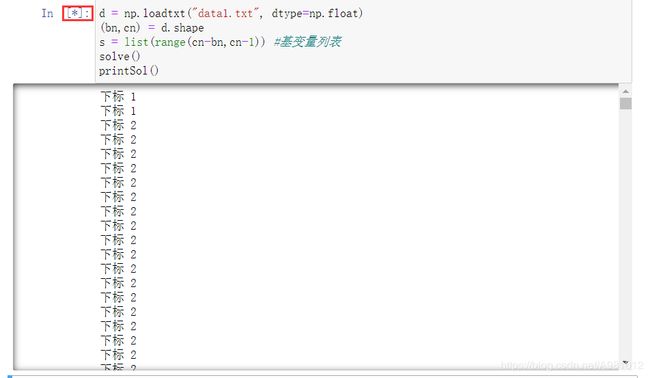
但是我用scipy库的代码进行运算的时候，得出的结果是有值输出，我不理解：

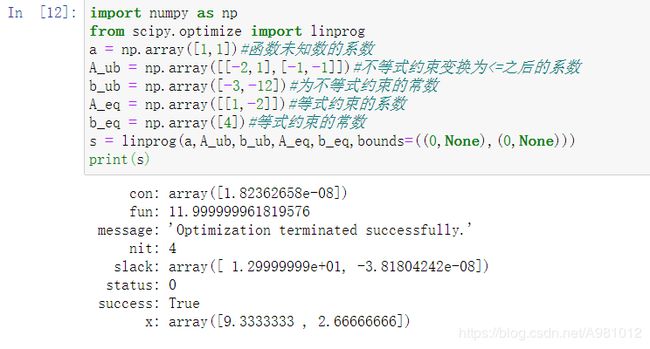
有知道的路过的大佬，方便的话告诉我一下。
如有错误请指正！
代码参考：线性规划：单纯形法python代码.