人工智能基础学习:Fisher判别的python推导和Fisher线性分类判断的理解
Fisher线性分类判断的理解和Fisher判别的python推导
- Fisher线性分类判断
- 类内离散度概念和几何意义
- 类间离散度概念和几何意义
- Fisher判别python推导
Fisher线性分类判断
Fisher线性判别函数是研究线性判别函数中最有影响的方法之一。对线性判别函数的研究就是从R.A.Fisher在1936年发表的论文开始的。
Fisher 线性判别函数的提出:在用统计方法进行模式识别时,许多问题涉及到维数,在低维空间行得通的方法,在高维空间往往行不通。因此,降低维数就成为解决实际问题的关键。Fisher的方法,就是解决维数压缩问题。
对xn的分量做线性组合可得标量
yn=wTxn ,n=1,2,…,Ni
这样便得到N个一维样本yn组成的集合。从而将多维转换到了一维。
Fisher线性判别分析的基本思想:选择一个投影方向(线性变换,线性组合),将高维问题降低到一维问题来解决,同时变换后的一维数据满足每一类内部的样本尽可能聚集在一起,不同类的样本相隔尽可能地远。
Fisher线性判别分析,就是通过给定的训练数据,确定投影方向W和阈值w0, 即确定线性判别函数,然后根据这个线性判别函数,对测试数据进行测试,得到测试数据的类别。
线性判别函数的一般形式可表示成 g ( X ) = W T X + w 0 ) g(X)=W^T X+w_0) g(X)=WTX+w0) 其中
X = ( x 1 . . . x d ) W = ( w 1 w 2 . . . w d ) X=\begin{pmatrix} x_1 \\\\ ... \\\\ x_d \end{pmatrix} W=\begin{pmatrix} w_1 \\\\ w_2 \\\\ ... \\\\ w_d \end{pmatrix} X=⎝⎜⎜⎜⎜⎛x1...xd⎠⎟⎟⎟⎟⎞W=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛w1w2...wd⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞
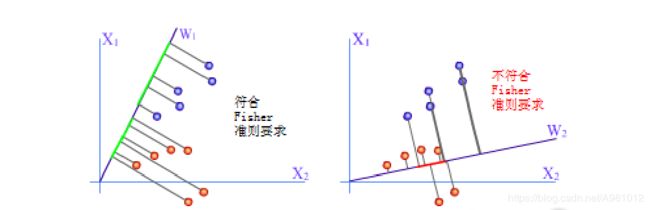
Fisher选择投影方向W的原则,即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开,类内样本投影尽可能密集的要求。
一、 首先确定类w
各类样本均值向量mi
m i = 1 N i ∑ x ∈ X i X , i = 1 , 2 m_i=\frac{1}{N_i}\sum_{x\in X_i} X,i=1,2 mi=Ni1x∈Xi∑X,i=1,2
在投影后的一维空间中,各类样本均值为 m i ‘ = W T m i m_i^`=W^Tm_i mi‘=WTmi,求类内离散度矩阵和类间离散度矩阵变换为一维空间后,就是类内离散度和类间离散度。
根据这些可以求出Fisher准则函数为
m a x J F ( W ) = ( m 1 ~ − m 2 ~ ) 2 S 1 ~ 2 + S 2 ~ 2 maxJ_F(W)=\frac{(\tilde{m_1}-\tilde{m_2})^2}{\tilde{S_1}^2+\tilde{S_2}^2} maxJF(W)=S1~2+S2~2(m1~−m2~)2
二、然后确定阈值
w 0 w_0 w0是一个常数,称为阈值权,对于两类问题的线性分类器可以采用这种决策规则:
令 g ( x ) = g 1 ( x ) − g 2 ( x ) g(x)=g_1(x)-g_2(x) g(x)=g1(x)−g2(x),如果g(x)>0,则决策 x ∈ w 1 x \in w_1 x∈w1,如果g(x)<0,则决策 x ∈ w 2 x \in w_2 x∈w2;如果g(x)=0,则可将x任意分到某一类,或拒绝。
三、进行Fisher线性判别的决策规则
Fisher的准则函满足连个性质:
1.投影后,各类样本内部尽可能密集,即总类内离散度越小越好。
2.投影后,各类样本尽可能离得远,即样本类间离散度越大越好。根据这个求解得到准则函数的最大值
可求出 w = S w − 1 ( m 1 , − m 2 ) w=S_w^{-1} (m_1,-m_2) w=Sw−1(m1,−m2)
这句就是Fisher判别准则下的最优投影方向。
四、最后得到决策规则
若 g ( x ) = W T ( x − 1 2 ( m 1 + m 2 ) ) > 或 < log P ( w 2 ) P ( w 1 ) , 则 x ∈ { w 1 w 2 g(x)=W^T(x-\frac{1}{2}(m_1+m_2))>或<\log \frac{P_(w_2)}{P_(w_1)},则x\in \lbrace {w_1}{w_2} g(x)=WT(x−21(m1+m2))>或<logP(w1)P(w2),则x∈{w1w2
若对于某一个未知类别的样本向量x,如果 y = W T , x > y > 0 y=W^T,x>y>0 y=WT,x>y>0,则 x ∈ w 1 x \in w_1 x∈w1;否则 x ∈ w 2 x \in w_2 x∈w2
类内离散度概念和几何意义
类内离散度刻画的是从总体来看类内各个样本与类之间(这里所刻画的类特性是由是类内各个样本的平均值矩阵构成)离散度

样本类内离散度矩阵 S i S_i Si为
S i = ∑ x ∈ X i ( X − m i ) ( X − m i ) T , i = 1 , 2 S_i=\sum_{x \in X_i } (X-m_i)(X-m_i)^T, i=1,2 Si=x∈Xi∑(X−mi)(X−mi)T,i=1,2
总类内离散度为
S w = S 1 + S 2 S_w=S_1+S_2 Sw=S1+S2
在投影后的一维空间中,样本类内离散度矩阵为
S i ‘ = W T S i W S_i^`=W^TS_iW Si‘=WTSiW ,总类内离散度为 S w ‘ = W T S W W S_w^`=W^TS_WW Sw‘=WTSWW
类间离散度概念和几何意义
类间离散度就是把所有样本中各个样本根据自己所属的类计算出样本与总体的协方差矩阵的总和,这从宏观上描述了所有类和总体之间的离散冗余程度。

样本类间离散度矩阵 S b S_b Sb为
S b = ( m 1 − m 2 ) ( m 1 − m 2 ) T S_b=(m_1-m_2)(m_1-m_2)^T Sb=(m1−m2)(m1−m2)T
在投影后的一维空间中,样本类间离散度矩阵为
S b ‘ = W T S b W S_b^`=W^TS_bW Sb‘=WTSbW
Fisher判别python推导
用Iris数据集为例,来进行Fisher判别的推导。 Iris数据集以鸢尾花的特征作为数据来源,数据集包含150个数据集,有4维,分为3 类,每类50个数据,每个数据包含4个属性,是在数据挖掘、数据分类中非常常用的测试集、训练集。
首先要导入需要的库和读取Iris数据集中的数据
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
import math
# prepare the data
iris = datasets.load_iris()
X = iris.data
y = iris.target
names = iris.feature_names
labels = iris.target_names
y_c = np.unique(y)
求出各类别的平均值
np.set_printoptions(precision=4)
mean_vector = [] # 类别的平均值
for i in y_c:
mean_vector.append(np.mean(X[y == i], axis=0))
print('Mean Vector class %s:%s\n' % (i, mean_vector[i]))
求出类内离散度和类间离散度
S_W = np.zeros((X.shape[1], X.shape[1]))
for i in y_c:
Xi = X[y == i] - mean_vector[i]
S_W += np.mat(Xi).T * np.mat(Xi)
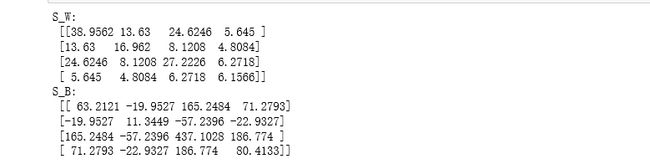
print('S_W:\n', S_W)
S_B = np.zeros((X.shape[1], X.shape[1]))
mu = np.mean(X, axis=0) # 所有样本平均值
for i in y_c:
Ni = len(X[y == i])
S_B += Ni * np.mat(mean_vector[i] - mu).T * np.mat(mean_vector[i] - mu)
print('S_B:\n', S_B)
然后求出W
eigvals, eigvecs = np.linalg.eig(np.linalg.inv(S_W) * S_B) # 求特征值,特征向量
np.testing.assert_array_almost_equal(np.mat(np.linalg.inv(S_W) * S_B) * np.mat(eigvecs[:, 0].reshape(4, 1)),
eigvals[0] * np.mat(eigvecs[:, 0].reshape(4, 1)), decimal=6, err_msg='',
verbose=True)
# sorting the eigenvectors by decreasing eigenvalues
eig_pairs = [(np.abs(eigvals[i]), eigvecs[:, i]) for i in range(len(eigvals))]
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)
W = np.hstack((eig_pairs[0][1].reshape(4, 1), eig_pairs[1][1].reshape(4, 1)))
X_trans = X.dot(W)
assert X_trans.shape == (150, 2)
plt.figure(figsize=(8, 4))
plt.subplot(121)
plt.scatter(X_trans[y == 0, 0], X_trans[y == 0, 1], c='r')
plt.scatter(X_trans[y == 1, 0], X_trans[y == 1, 1], c='g')
plt.scatter(X_trans[y == 2, 0], X_trans[y == 2, 1], c='b')
plt.title('my LDA')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.legend(labels, loc='best', fancybox=True)
最后进行判别并输出正确率
直接用Iris数据集里的 划分为三类,然后判断准确率
from sklearn import discriminant_analysis
from sklearn.model_selection import train_test_split
import numpy
data = numpy.genfromtxt('iris.data', delimiter=',', usecols=(0,1,2,3))
target = numpy.genfromtxt('iris.data', delimiter=',', usecols=(4), dtype=str)
t = numpy.zeros(len(target))
t[target == 'Iris-setosa'] = 1
t[target == 'Iris-versicolor'] = 2
t[target == 'Iris-virginica'] = 3
clf = discriminant_analysis.LinearDiscriminantAnalysis()
train, test, t_train, t_test = train_test_split(data, t, test_size=0.5, random_state=0)
clf.fit(train, t_train)
print(clf.score(test,t_test))
最后输出为![]()
如有错误请指正!
参考博客:https://blog.csdn.net/pengjian444/article/details/71138003
https://blog.csdn.net/mengjizhiyou/article/details/103309372.