采用线性LDA、k-means和SVM算法对鸢尾花数据集和月亮数据集进行二分类可视化分析

SVM，k-means，线性LDA算法简介

SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。
k-means是将对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。
线性LDA是将数据投影到低维空间之后，使得同一类数据尽可能的紧凑，不同类的数据尽可能分散。

对两个数据集采用线性LDA进行分类

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

# 读取数据，并提取花瓣长度和宽度特征
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width

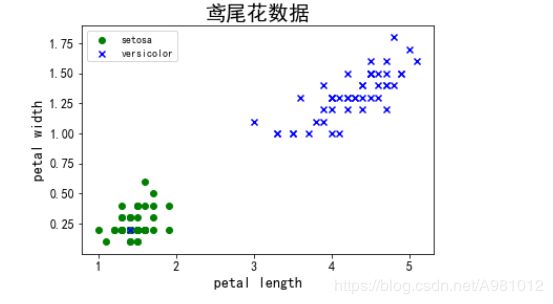
plt.scatter(X[:49, 0], X[:49, 1], color='green', marker='o', label='setosa')
plt.scatter(X[49:99, 0], X[49: 99, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc='upper left')
plt.title("鸢尾花数据",fontsize=20)
plt.show()

结果显示：

月亮数据集分类有错误，没有进行分类，等待修改

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)

def plot_dataset(X, y, axes):
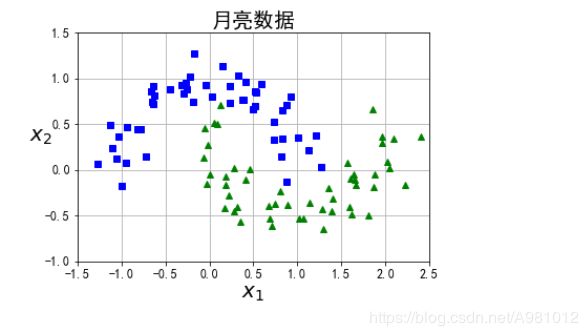
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
    plt.title("月亮数据",fontsize=20)

plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()

结果显示：

采用k-means进行分类

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.cluster import KMeans

# 读取数据，并提取花瓣长度和宽度特征
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
x_axis = iris["data"][:, (2)]

y_axis = iris["data"][:, (3)]
model = KMeans(n_clusters=2)

#训练模型
model.fit(X)
#选取行标为150的那条数据，进行预测
prddicted_label= model.predict([[71.67, 74]])
#预测全部数据

all_predictions = model.predict(X)
#all_predictions=np.array(all_predictions).reshape(-1,1)
#打印出来数据的聚类散点图
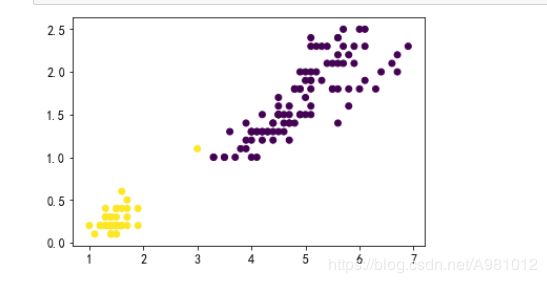
plt.scatter(x_axis,y_axis,c=all_predictions)
plt.show()

结果显示：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
x_axis=X[:,0]
y_axis=X[:,1]
model = KMeans(n_clusters=2)

#训练模型
model.fit(X)
#选取行标为100的那条数据，进行预测
prddicted_label= model.predict([[0.12784118,  0.7055097 ]])
#预测全部数据

all_predictions = model.predict(X)
#all_predictions=np.array(all_predictions).reshape(-1,1)
#打印出来数据的聚类散点图
plt.scatter(x_axis,y_axis,c=all_predictions)
plt.show()

结果显示：

采用SVM算法进行分类

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

X, y = make_moons(n_samples=100, noise=0.15, random_state=42)

polynomial_svm_clf = Pipeline([
        # 将源数据 映射到 3阶多项式
        ("poly_features", PolynomialFeatures(degree=3)),
        # 标准化
        ("scaler", StandardScaler()),
        # SVC线性分类器
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
    ])
polynomial_svm_clf.fit(X, y)
import numpy as np
def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
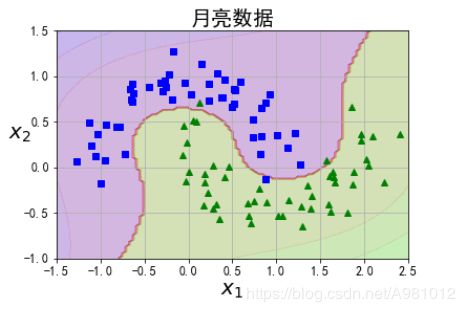
    plt.title("月亮数据",fontsize=20)
def plot_predictions(clf, axes):
    # 打表
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)

    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()

结果为：

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

# 读取数据，并提取花瓣长度和宽度特征
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
# 二分类
y = (iris["target"] == 2).astype(np.float64)  # Iris-Virginica
scaler = StandardScaler()
# 构建两个svc线性分类器，一个C为1 一个C为100
svm_clf1 = LinearSVC(C=100, loss="hinge", random_state=42)

scaled_svm_clf1 = Pipeline([
        ("scaler", scaler),
        ("linear_svc", svm_clf1),
    ])
scaled_svm_clf1.fit(X, y)
# Convert to unscaled parameters
# 将标准化的参数转化为未标准化的
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf1.coef_ = np.array([w1])

# Find support vectors (LinearSVC does not do this automatically)
t = y * 2 - 1
support_vectors_idx1 = (t * (X.dot(w1) + b1) < 1).ravel()
svm_clf1.support_vectors_ = X[support_vectors_idx1]
plt.figure(figsize=(12,3.2))
plt.subplot(121)
# 画数据点
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Iris-Virginica")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs", label="Iris-Versicolor")
# 画svc的决策边界
plot_svc_decision_boundary(svm_clf1, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
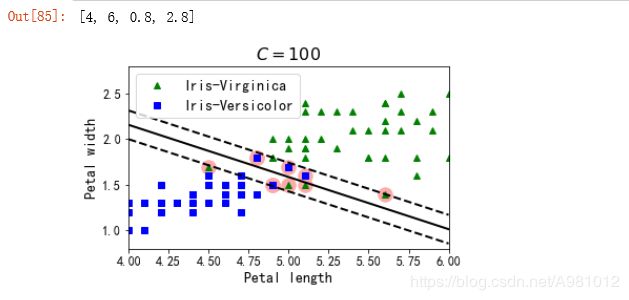
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])

结果显示：

SVM算法的优点

解决高维特征的分类问题和回归问题很有效,在特征维度大于样本数时依然有很好的效果。
仅仅使用一部分支持向量来做超平面的决策，无需依赖全部数据。
有大量的核函数可以使用，从而可以很灵活的来解决各种非线性的分类回归问题。
样本量不是海量数据的时候，分类准确率高，泛化能力强。

如有错误请指正！