一、概述
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个典型应用。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段之间有序。将两个有序表合并成一个有序表,称为二路归并。
二、归并排序的基本思想
将待排序序列R[0...n-1]看成是n个长度为1的有序序列,将相邻的有序表成对归并,得到n/2个长度为2的有序表;将这些有序序列再次归并,得到n/4个长度为4的有序序列;如此反复,最后得到一个长度为n的有序序列。
归并排序需要做两件事:
1)分解:将序列每次折半划分
2)合并:将划分后的序列段两两合并后排序
如何合并?
在每次合并过程中,都是对两个有序的序列段进行合并,然后再排序。这两个有序的序列段分别为R[low, mid]和R[mid+1, high],先将它们合并到一个局部的暂存数组R2中,待合并完成后再将R2复制回R中。
每次从两个段中取出一个记录进行关键字的比较,将较小者放入R2中,最后将各段中余下的部分直接复制到R2中。经过这样的过程,R2已经是一个有序的序列,再将其复制回R中,一次合并排序就完成了。
在某趟归并中,设各子表的长度为gap,则归并前R[0...n-1]中共有n/gap个有序的子表:R[0...gap-1], R[gap...2*gap-1], ... , R[(n/gap)*gap ... n-1]。
在将相邻的子表归并时,需要对表的特殊情况进行处理:
1)若子表个数为奇数,最后一个子表无须和其他子表归并(即本趟处理轮空);
2)若子表个数为偶数,到最后一对子表中后一个子表区间的上限为n-1;
三、排序性能
时间复杂度:归并排序的形式就是一棵二叉树,需要遍历的次数就是二叉树的深度,时间复杂度是O(nlogn)。
空间复杂度:算法处理过程中,需要一个大小为n的临时存储空间用来保存合并序列。
算法稳定性:在归并排序中,相等元素的顺序不会改变,所以它是稳定的算法。
总结:
1)时间复杂度:O(nlogn)
2)空间复杂度:O(n)
3)稳定性:稳定
4)复杂性:较复杂
四、选择对比
1)空间复杂度考虑:选择优先级为[堆排序>快速排序>归并排序]。
2)稳定性考虑:应选归并排序,堆排序和快速排序都是不稳定的。
3)平均排序速度考虑:应选快速排序。
五、代码实现
import java.util.Arrays;
/**
* 归并排序
* 效率O(nlogn),归并的最佳、平均和最糟用例效率之间没有差异,适用于排序大列表,基于分治法。
*/
public class MergeSort {
public static void main(String[] args) {
int[] array = {9, 1, 5, 3, 4, 2, 6, 8, 7};
MergeSort merge = new MergeSort();
System.out.println("排序前:"+Arrays.toString(array));
merge.sort(array);
System.out.println("排序后:"+Arrays.toString(array));
}
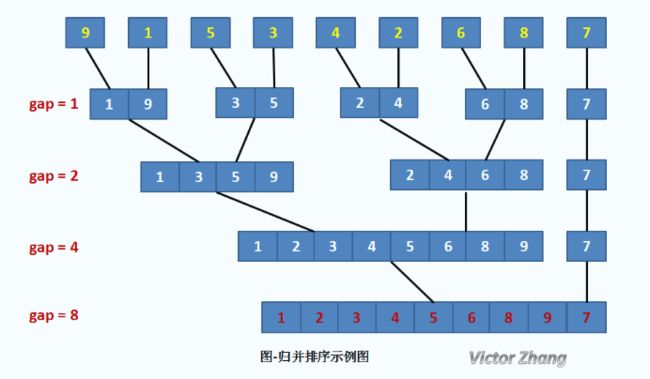
private static int[] sort(int[] list){
for(int gap = 1;gap MergePass(list,gap,list.length); System.out.println("gap="+gap+":"+Arrays.toString(list)); } return list; } private static void MergePass(int[] arr,int gap,int length){ int i=0; // 归并gap长度的两个相邻子表 for(i=0;i+2*gap-1 < length;i = i+2*gap){ Merge(arr, i, i + gap - 1, i + 2 * gap - 1); } // 余下两个子表,后者长度小于gap if (i + gap - 1 < length) { Merge(arr, i, i + gap - 1, length - 1); } } private static void Merge(int[] arr,int low,int mid,int high){ int i=low;// i是第一段序列的下标 int j = mid +1;// j是第二段序列的下标 int k = 0;// k是临时存放合并序列的下标 int[] array2 = new int[high - low + 1]; // array2是临时合并序列 // 扫描第一段和第二段序列,直到有一个扫描结束 while (i <= mid && j <= high) { // 判断第一段和第二段取出的数哪个更小,将其存入合并序列,并继续向下扫描 if (arr[i] <= arr[j]) { array2[k] = arr[i]; i++; k++; } else { array2[k] = arr[j]; j++; k++; } } // 若第一段序列还没扫描完,将其全部复制到合并序列 while(i <= mid){ array2[k] = arr[i]; i++; k++; } // 若第二段序列还没扫描完,将其全部复制到合并序列 while(j <= high){ array2[k] = arr[j]; j++; k++; } // 将合并序列复制到原始序列中 for (k = 0, i = low; i <= high; i++, k++) { arr[i] = array2[k]; } } } 运行结果: 排序前: 9 1 5 3 4 2 6 8 7 gap = 1: 1 9 3 5 2 4 6 8 7 gap = 2: 1 3 5 9 2 4 6 8 7 gap = 4: 1 2 3 4 5 6 8 9 7 gap = 8: 1 2 3 4 5 6 7 8 9 排序后: 1 2 3 4 5 6 7 8 9