图之从一个顶点到其余各个顶点的最短路径(有向图)
目录
- 从一个顶点到其余各个顶点最短路径的简介
- 举例以及详细分析
- 代码块
- 测试结果
从一个顶点到其余各个顶点最短路径的简介(又名单元最短路径)
1.定义概览
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。注意该算法要求图中不存在负权边。
问题描述:在无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短路径。(单源最短路径)
算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
举例以及详细分析

a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则(u,v)正常有权值,若u不是v的出边邻接点,则(u,v)权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
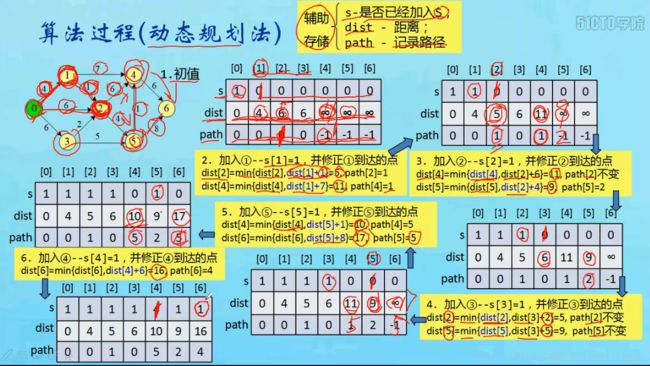
首先先定义三个辅助数组:
int s[MAX]用来表示这个顶点是否加入了最短距离路径。
int dist[MAX]用来表示起始点到这个顶点的最短路径是多少。
int path[MAX]用来表示这个顶点的上一个顶点是什么,即表示的是路径。
初始化时 假设其实点是v
s[MAX]存放的都是0,表示还未有顶点加入最短路径。dist[MAX]存放的是起始点与其邻接点的最短距离即g->edges[v][j],不是起始点的邻接点的顶点用∞表示。path[MAX]存放的也都是v,表示都是从起始点v开始的,如果顶点与起始点没有直接联系则用-1表示。
又因为起始点为v,所以初始化的最后s[v]=1,path[v]=0;
之后在dist[]中找到(dist[i]最小的并且s[i]==0)的顶点,作为最短路径的下一个顶点(下标为u),并将其s[u]变为1。
找到下一个顶点后,图的最短路径可能发生了相应的变化;将新顶点与其他s[i]!=0的顶点进行联立,寻找他们之间的最小路径并改变其相应的path[],dist[]的值。

在最后的输出函数中必须严格遵守递归规则

红圈中的顺序不能颠倒否则输出的数值中
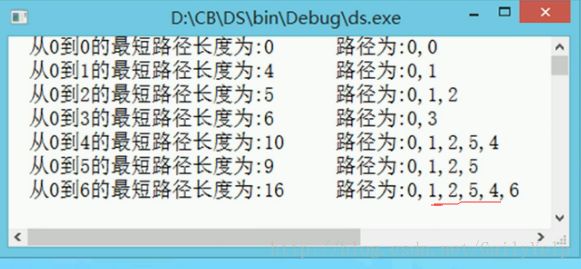
划线部分会输出逆序(请自行体会);
代码块
#includen; i++)
{
scanf("%d%d", &(G->vexs[i].no), &(G->vexs[i].info));
}
for (i = 0; in; i++)
{
for (j = 0; jn; j++)
{
if (i == j)
{
G->edges[i][j] = 0;
}
else
{
G->edges[i][j] = LIMITLESS;
}
}
}
printf("请输入 图的顶点 边和它的权值:\n");
for (k = 0; ke; k++)
{
scanf("%d%d%d", &start, &end, &w);
G->edges[start][end] = w;
}
}
void print(MGraph *G)
{
int i, j;
printf("顶点数:%d, 边数:%d\n", G->n, G->e);
printf("%d个顶点的信息:\n", G->n);
for (i = 0; in; i++)
{
printf("%5d%5d", G->vexs[i].no, G->vexs[i].info);
}
printf("\n各个顶点的连接情况:\n");
printf("\t");
for (i = 0; in; i++)
{
printf("[%d]\t", i);
}
printf("\n");
for (i = 0; in; i++)
{
printf("[%d]\t", i);
for (j = 0; jn; j++)
{
if (G->edges[i][j] == LIMITLESS)
{
printf("oo\t");
}
else
{
printf("%d\t", G->edges[i][j]);
}
}
printf("\n");
}
}
void Ppath(int path[], int i, int v) //前向递归查找路径上的顶点
{
int k;
k = path[i];
if (k == v)
{
return;
}
Ppath(path, k, v);
printf("%d", k);
}
void Dispath(int dist[], int path[], int s[], int n, int v)
{
int i;
for (i = 0; i < n; i++)
{
if (s[i] == 1)
{
printf("从%d到%d的最短路径长度为:%d\t路径为:", v, i, dist[i]);
printf("%d", v);//输出路径上的起点
Ppath(path, i, v); //输出路径上的中间点
printf("%d\n", i);//输出路径上的终点
}
else
{
printf("从%d到%d不存在路径\n", v, i);
}
}
}
void Dijkstra(MGraph *g, int v)
{
int mindis, i, j, u;
int s[MAXV]; //表示这个顶点是否存入最短路线中
int dist[MAXV];//表示起始点到此顶点的距离
int path[MAXV];//表示此点的上一步是哪一个顶点
for (i = 0; i < g->n; i++)
{
s[i] = 0;
dist[i] = g->edges[v][i];
if (g->edges[v][i] < LIMITLESS)
{
path[i] = v;
}
else
{
path[i] = -1;
}
}
s[v] = 1;
path[v] = 0;
for (i = 0; i < g->n; i++)
{
mindis = LIMITLESS;//mindis置最小长度初值
for (j = 0; j < g->n; j++) //选取不在s中且具有最小距离的顶点u
{
if (s[j] == 0 && dist[j] s[u] = 1;
for (j = 0; j < g->n; j++)
{
if (s[j] == 0)
{
if (g->edges[u][j] < LIMITLESS&&dist[u] + g->edges[u][j] < dist[j])
{
dist[j] = dist[u] + g->edges[u][j];
path[j] = u;
}
}
}
}
Dispath(dist, path, s, g->n, v);
}
int main(void)
{
MGraph *g;
g = malloc(sizeof(MGraph));
creat(g);
print(g);
Dijkstra(g, 0);
system("pause");
return 0;
}