GrowingIO 大数据多维分析自动化测试实践
作者:郝阔君 GrowingIO QA Lead,曾任职于中国惠普、奇虎 360。带领 QA 团队负责 GrowingIO
全产品线质量保证工作,目前专注于 DevOps 实践,帮助团队提升质量和效率。
1.问题背景
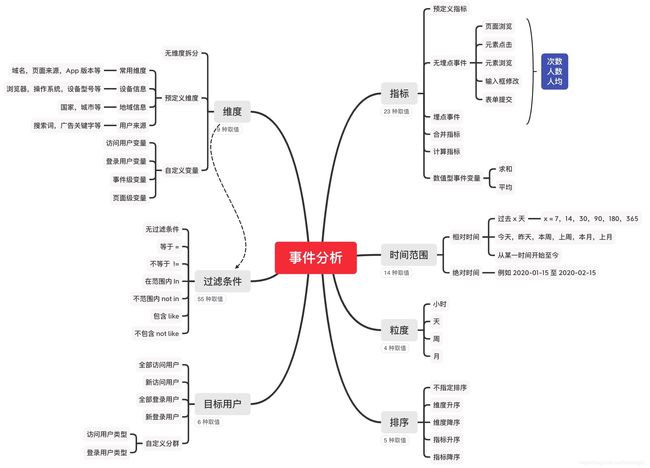
「事件分析」是 GrowingIO 为用户提供的一个非常灵活、强大的基于大数据平台的交互式多维分析工具,下面是一个简单的单指标、单维度、带过滤条件的事件分析图表:
如何对事件分析产生的图表进行测试呢?经过分析,我们发现一个事件分析图表包含指标、维度、目标用户、过滤条件、时间范围、粒度、排序多个因素,这些因素会影响其查询结果。
而每个因素又有多个取值,有的取值多达几十种,即使每个因素都使用等价类划分取最小值,其组合产生的测试用例数为:
指标数(23) * 维度数(9) * 目标用户数(6) * 过滤条件(无过滤条件(1) + 维度数(9) * 过滤类型(6)=55) * 时间范围(14) * 粒度(4) * 排序(5) = 22314600。
即使仅选取其中最关键的指标、维度、目标用户、过滤条件 4 个因素,其组合数也高达 23 * 9 * 7 * 55 = 79695 。如此多的测试用例数量,如何测试呢?
2.寻找测试方案
显然,通过手工测试的方式是无法完成如此海量的测试任务的,必然需要使用自动化测试的方式。但如果采用 UI 自动化方式,其实现成本高,执行慢,不稳定,结果判定难, API 测试显然更合适。
GrowingIO 的可视化图表数据都来自 Charts 服务,Charts 服务定义了一种强大灵活的被称为 GQL(GrowinIO Query Language) 的 DSL,用于描述图表查询(可以类比 SQL)。以上面事件分析图表为例其 GQL 简化的表达如下:
{
"metrics": [
{
"id": "pv",
"name": "页面浏览量"
}
],
"dimensions": [
"city"
],
"granularities": [
{
"id": "tm",
"interval": 86400000
}
],
"filter": {
"op": "and",
"exprs": [
{
"key": "bw",
"op": "=",
"values": [
"Chrome"
],
"name": "浏览器"
}
]
},
"orders": null,
"timeRange": "day:8,1",
"targetUser": "uv",
"limit": 20
}
返回结果如下:
{
"data": [
[
"北京",
1111
],
[
"上海",
2222
],
[
"深圳",
3333
],
[
"杭州",
4444
],
[
"广州",
5555
]
],
"meta": {
"columns": [
{
"id": "city",
"name": "城市",
"isDim": true,
"isRate": false,
"isDuration": false
},
{
"id": "pv",
"name": "页面浏览量",
"isDim": false,
"isRate": false,
"isDuration": false
}
]
}
}
熟悉了接口请求的结构,实现接口自动化就比较容易了,只需选取合适的测试数据,构造请求,发送请求,验证结果。
但在实现自动化测试的时候,不免疑惑:这真的是好的方案吗?
经过简单计算我们发现,即使选择较少的覆盖 79695 条用例,假设平均每个执行 10 秒钟,也需要耗时 221.375 个小时。当然可以采用并行执行加速,并行 100 个进程,每次也需要执行 2.2 小时。
2 个小时似乎还可以接受,但是实际执行发现,测试执行的稳定性很难保证,主要原因是分析数据都来自后端的 OLAP 系统,其数据量相当庞大,很难承受如此高密度的频繁查询。
此外,如此多的用例真的都是有效覆盖吗?执行这么多用例实际发现缺陷的可能性又有多少?ROI 又是多少?实际上,这几个问题很难给出精确的答案,需要不断地执行测试,统计其发现的缺陷才能给出答案。
3.更好的解决方案
使用最少的用例,发现尽可能多的缺陷,是测试用例设计追求的目标,也是测试工程师价值所在。
上面的测试用例使用了全组合的方式进行覆盖,如果使用更少的因素组合必将大大减少用例数量,但是减少组合数能否保证测试效果?答案是肯定的。
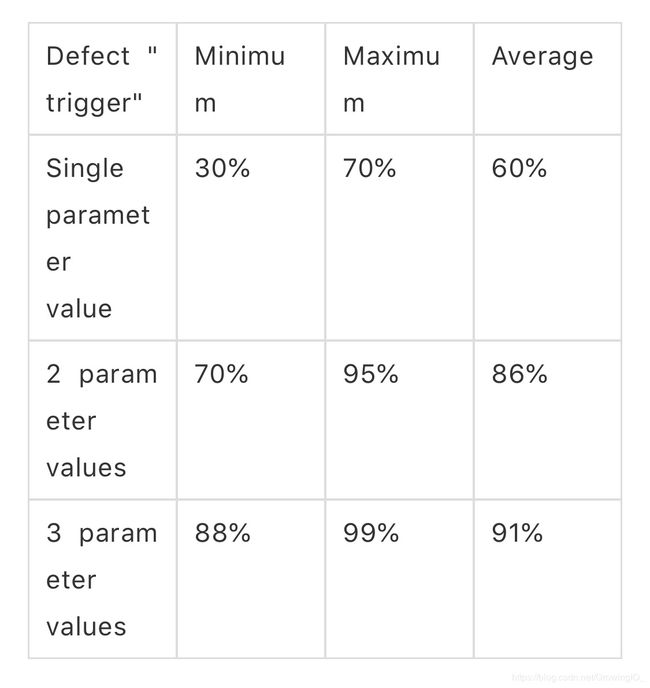
据了解,IEEE 根据交付给客户的软件系统中漏测缺陷的特征分析,发表了回顾性研究结果:
其研究结果指出,很少有缺陷是由 4 个和 5 个参数相互作用引起的,6 个参数相互作用引起的缺陷更是罕见。
关键结论:平均超过 90% 以上缺陷是由 3 个或更少的参数组合引起的。因此任何测试设计中都应该至少保证两因素组合的 100% 的覆盖测试。有着高可靠性需求的应用,比如医疗设备或者航空电子设备,应该保证至少 3-way 因素组合的 100% 的覆盖测试。
由于两因素组合测试在测试用例个数和错误检测能力上达到了较好的平衡,它是目前主流的组合测试方法。
那么如何有效地生成两因素组合的测试用例呢?这个已经有前辈给出了方法和工具。对于多输入参数组合类的测试方法,目前业界主要有两种测试用例设计方法,成对测试 (Pairwise Testing) 和正交表测试 (OAT: Orthogonal Array Testing)。
由于我们现有的自动化 API 测试都是使用 Python 语言实现的,并且有一个开源的 Python 库 allpairspy 可以很容易的实现成对测试用例生,所以很自然的就选择了这个工具。
4.Pairwise Testing 应用
Pairwise Testing 又被称为全对测试(All-Pairs Testing), 是软件测试的组合方法,对于软件系统中的每对输入参数对,它们都将测试这些参数的所有可能离散组合。
通过“并行化”参数对的测试,使用精心选择的测试向量,可以比穷举搜索所有参数的所有组合更快地完成操作。简单地说,就是保证所因素的的变量都至少两两组合一次。
Pairwise Testing 例子
仍然以上面事件分析为例,为了方便说明做一些简化,假设有下面指标、维度和目标用户组合。
采用全组合将生成 27 条测试用例:
使用 Pairwise Testing 筛选后的组合,保证指标和维度,指标与目标用户,维度与目标用户两两组合都覆盖,用例数减少到 9 条,下面是其中一种排列方式,需要注意的是同一组输入可以输出多组个满足 Pairwise 的结果,其测试效果等价。
from allpairspy import AllPairs
M = ['M1','M2','M3']
D = ['D1','D2','D3']
U = ['U1','U2','U3']
parameters = [M,D,U]
print("PAIRWISE:")
for i, pairs in enumerate(AllPairs(parameters)):
print("|{}|{}|{}|{}|".format(i, *pairs))
使用 piarwise 对事件分析用例进行优化
下面是一段简单的测试脚本,对事件分析所有组合用例使用 AllPairs 生成的用例数进行计算。经计算其组合数为 1269, 仅占原来 22314600 种组合的 0.0057%,极大的减少了用例数。
from allpairspy import AllPairs
def get_arrays(*values):
r = []
for d in values:
r.append(range(d))
return r
print(len(list(AllPairs(get_arrays(23,9,7,55,14,4,5),filter_func=is_valid_combination))))
5.进一步优化
通过上面实验,测试用例里数已经大大减少了,但是根据实际业务和测试需要我们可以进行进一步的优化,来提升测试效果。
根据业务规则过滤
上面用例没有考虑各个因素之间的相互关系,比如仅有指标为埋点事件时,维度值和过滤条件才可以为事件变量。allpairspy 支持对组合结果进行自定义过滤。下面是一段模拟代码,模拟量非法组合的过滤,经过计算有效组合为 954 个,又在原来基础上减少了近 1/4 。
from allpairspy import AllPairs
def get_arrays(*values):
r = []
for v in values:
r.append(range(v))
return r
def is_valid_combination(row):
n = len(row)
if n > 1:
# 假设指标 1 是埋点事件,维度 1 为事件变量
if 1 == row[0] and 1 != row[1]:
return False
if n > 3:
# 假设指标 1 是埋点事件,过滤条件中有 6 个是埋点事件相关
if 1 == row[0] and row[3] < 6:
return False
return True
print(len(list(AllPairs(get_arrays(23,9,7,55,14,4,5)))))
每次生成不同的组合
同样的因素变量满足 Pairwise 的组合不止一种,如果每次生成的测试用例组合都不一样,那么随着测试的执行次数增加,会不断的测试新的组合,更有可能发现某些特定组合的缺陷,提升测试效果。很遗憾 allpairspy 没有提供随机种子的参数,每次生成的用例组合都相同。
不过在生成测试用例前先随机打乱每个因素的变量值顺序,即可实现。可以用一下代码验证,每次生成的用例组合都会发生变化。
from allpairspy import AllPairs
from random import shuffle
M = ['M1','M2','M3']
D = ['D1','D2','D3']
U = ['U1','U2','U3']
shuffle(M)
shuffle(D)
shuffle(U)
parameters = [M,D,U]
print("PAIRWISE:")
for i, pairs in enumerate(AllPairs(parameters)):
print("|{}|{}|{}|{}|".format(i, *pairs))
N-wise 组合覆盖
上面都是 Pairwise (即 2-wise) 组合覆盖,如果因素和变量较少时可以增加到 3-wise 甚至更多组合,以提升覆盖率。allpairspy 支持生成 n-wise 组合,只需要在其构造参数添加 n=x 参数即可,示例如下:
from allpairspy import AllPairs
M = ['M1','M2','M3']
D = ['D1','D2','D3']
U = ['U1','U2','U3']
F = ['F1','F2','F3','F4']
parameters = [M,D,U,F]
print("PAIRWISE:")
for i, pairs in enumerate(AllPairs(parameters,n=2)):
print("|{}|{}|{}|{}|{}|".format(i, *pairs))
print("3-WISE:")
for i, pairs in enumerate(AllPairs(parameters,n=3)):
print("|{}|{}|{}|{}|{}|".format(i, *pairs))
6.Pairwise 的不足
没有银弹,任何测试方法都不可能 100% 的发现所有缺陷,Pairwise 方法也存在一定的不足。
- Pairwise对于因素的选择,需要对业务很熟悉,了解各个因素对输出的影响,以及各个因素之间的相互约束关系。如果构造的输入不正确,也难达到预期测试效果。
- Pairwise 算法对于多于 2 个因素相互作用所产生的 Bug 没有覆盖到,可以使用 N-wise
一定程度上解决,但是又会增加用例数,提高测试成本,实际使用中要综合考量。
但是综合考虑成本、效率和测试覆盖等因素,当前其仍然是组合测试领域的优秀解决方案。
参考文档:
《Pairwise Testing》
《allpairspy 》
《OATS PK Pairwise Testing》
《深入浅出 pairwise 算法》
《组合测试从理论到实践——从吃货的角度实现组合测试用例的自动设计》