机器学习 第9章 聚类 概念总结和简单实践

一  解决的问题

聚类属于无监督学习中的方法，目的在于在未标注label的数据集中找到潜在规律，并将数据进行聚类。

因为没有给定label，基本流程都是先随机产生样本作为计算中心，计算其他样本与中心的距离，距离近的划为同类；

迭代簇的数据中心，再进行下一轮计算，直到簇内数据不再变化或者达到停止条件，比如到达设定的簇数。

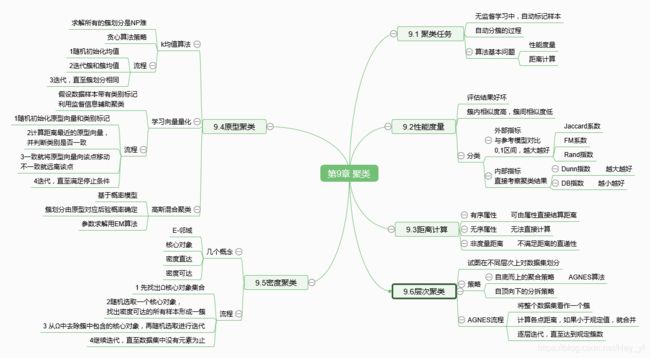
二 概念总结

三 习题

题9.4 基于西瓜集4.0设置三组不同k值，三组不同初始中心点，进行比较。讨论什么样的初始中心有利于取得好结果。

import pandas as pd
data = pd.read_csv('./CH9-DATA4.0.csv')
from sklearn.cluster import KMeans
import numpy as np
X = np.array(data)
# 不同簇数设置
kmeans1 = KMeans(n_clusters=3, random_state=0).fit(X)
kmeans2 = KMeans(n_clusters=4, random_state=0).fit(X)
kmeans3 = KMeans(n_clusters=5, random_state=0).fit(X)

# 绘图网格点准备
h = 0.01
x_max,x_min = max(data.density)+0.1,min(data.density)-0.1
y_max,y_min = max(data.sweety)+0.1, min(data.sweety)-0.1
xx , yy =  np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z1 = kmeans1.predict(np.c_[xx.ravel(), yy.ravel()])
Z1 = Z1.reshape(xx.shape)
Z2 = kmeans2.predict(np.c_[xx.ravel(), yy.ravel()])
Z2 = Z2.reshape(xx.shape)
Z3 = kmeans3.predict(np.c_[xx.ravel(), yy.ravel()])
Z3 = Z3.reshape(xx.shape)

# 绘制不同簇数的边界
import matplotlib.pyplot as plt 
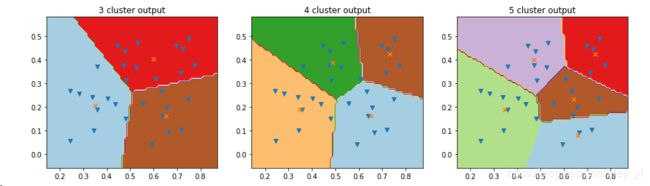
f, (ax1, ax2,ax3) = plt.subplots(1, 3, figsize=(15, 4))
ax1.set_title('3 cluster output')
ax1.contourf(xx, yy, Z1, cmap=plt.cm.Paired)
ax1.scatter( X[:,0], X[:,1], marker = 'v' )
centroids1 = kmeans1.cluster_centers_
ax1.scatter(centroids1[:, 0], centroids1[:, 1], marker='x')

ax2.set_title('4 cluster output')
ax2.contourf(xx, yy, Z2, cmap=plt.cm.Paired)
ax2.scatter( X[:,0], X[:,1], marker = 'v' )
centroids2 = kmeans2.cluster_centers_
ax2.scatter(centroids2[:, 0], centroids2[:, 1], marker='x')

ax3.set_title('5 cluster output')
ax3.contourf(xx, yy, Z3, cmap=plt.cm.Paired)
ax3.scatter( X[:,0], X[:,1], marker = 'v' )
centroids3 = kmeans3.cluster_centers_
ax3.scatter(centroids3[:, 0], centroids3[:, 1], marker='x')
plt.show()

# 同理，绘制不同初始状态的边界
kmeans4 = KMeans(n_clusters=5, random_state=0).fit(X)
kmeans5 = KMeans(n_clusters=5, random_state=10).fit(X)
kmeans6 = KMeans(n_clusters=5, random_state=20).fit(X)
Z4 = kmeans4.predict(np.c_[xx.ravel(), yy.ravel()])
Z4 = Z4.reshape(xx.shape)
Z5 = kmeans5.predict(np.c_[xx.ravel(), yy.ravel()])
Z5 = Z5.reshape(xx.shape)
Z6 = kmeans6.predict(np.c_[xx.ravel(), yy.ravel()])
Z6 = Z6.reshape(xx.shape)
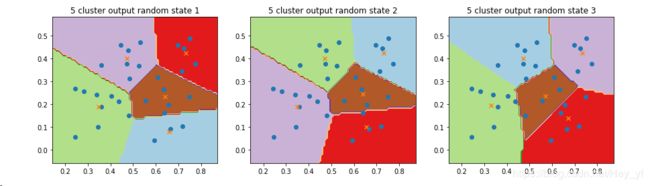
f, (ax4, ax5,ax6) = plt.subplots(1, 3, figsize=(15, 4))
ax4.set_title('5 cluster output random state 1')
ax4.contourf(xx, yy, Z4, cmap=plt.cm.Paired)
ax4.scatter( X[:,0], X[:,1], marker = 'o' )
# ax4.scatter( X[27,0], X[27,1], marker = 'v' )
# ax4.scatter( X[12,0], X[12,1], marker = 'v' )
# ax4.scatter( X[24,0], X[24,1], marker = 'v' )
# ax4.scatter( X[28,0], X[28,1], marker = 'v' )
# ax4.scatter( X[13,0], X[13,1], marker = 'v' )
centroids4 = kmeans4.cluster_centers_
ax4.scatter(centroids4[:, 0], centroids4[:, 1], marker='x')

ax5.set_title('5 cluster output random state 2')
ax5.contourf(xx, yy, Z5, cmap=plt.cm.Paired)
ax5.scatter( X[:,0], X[:,1], marker = 'o' )
# ax5.scatter( X[18,0], X[18,1], marker = 'v' )
# ax5.scatter( X[1,0], X[1,1], marker = 'v' )
# ax5.scatter( X[13,0], X[13,1], marker = 'v' )
# ax5.scatter( X[15,0], X[15,1], marker = 'v' )
centroids5 = kmeans5.cluster_centers_
ax5.scatter(centroids5[:, 0], centroids5[:, 1], marker='x')

ax6.set_title('5 cluster output random state 3')
ax6.contourf(xx, yy, Z6, cmap=plt.cm.Paired)
ax6.scatter( X[:,0], X[:,1], marker = 'o' )
# ax6.scatter( X[28,0], X[28,1], marker = 'v' )
# ax6.scatter( X[23,0], X[23,1], marker = 'v' )
# ax6.scatter( X[21,0], X[21,1], marker = 'v' )
# ax6.scatter( X[25,0], X[25,1], marker = 'v' )
# ax6.scatter( X[24,0], X[24,1], marker = 'v' )
centroids6 = kmeans6.cluster_centers_
ax6.scatter(centroids6[:, 0], centroids6[:, 1], marker='x')
plt.show()

不同簇数边界比较：

不同初始状态比较：