论文分享 -- >Graph Embedding -- >struc2vec

博客内容将首发在微信公众号"跟我一起读论文啦啦"，上面会定期分享机器学习、深度学习、数据挖掘、自然语言处理等高质量论文，欢迎关注！

本次要总结和分享的论文是struc2vec，参考的代码code，不同于以往根据顶点在图中位置以及与其他顶点距离关系来学习顶点的表示，本论文提出的一种独立于顶点位置，属性的方法来捕捉顶点的stronger notions of structural identity，并且学习到顶点之间的structural similarity。这样对于距离很远的相似顶点，也能学习到相似的潜在表示。

论文动机以及创新点

• 以往的 state-of-the-art 图表示方法，都是根据顶点在图中位置以及与其他顶点距离关系来学习顶点的表示，对于距离很远的相似顶点，无法很好的适用。

• 大量的实验表明，对于现有节点表示学习的state-of-the-art 方法，未能捕捉到顶点间structural similarity和structural equivalence，而struc2vec在对此能有更优异的表现。

• 本论文提出一种无监督的方法来捕捉顶点的 structural identity，该方法简称为struc2vec，主要有以下三个点：

  1. 独立于顶点标签和边属性及其在网络中的位置来学习节点之间的结构相似性。该方法可以判断相距很远，并在不同子图中识别结构相似的顶点。
  2. 建立一个多层结构图（multilayer graph）来衡量顶点间的结构相似性，层次越高，对structural similarity越严格。特别是，在层次的底部，顶点之间的结构相似性仅取决于它们的度，而在层次的顶部，相似性则取决于整个网络（从顶点的角度）。
  3. 为顶点生成随机上下文，这些节点是通过遍历多层结构图（注意：是构建的multilayer graph，而不是原始图网络）的加权随机游动观察到的结构相似的顶点序列。因此，经常出现的具有相似上下文的两个节点可能具有相似的结构。语言模型可以利用这种上下文来学习顶点的潜在表示。

struc2vec

主要有以下步骤：

1. 由原图，构建带权重的多层结构图（multilayer graph），每个层次都表示在不同跳数（layer）上的一个无向图，无向图上每两个顶点都是相连的，其中边的权重由该相邻顶点的度序列的相似度决定，度序列越相似边权重越大。相同顶点在不同层次（layer）上是相连的。
2. 在构建好的multilayer graph上进行带权重的随机游走，构建顶点的上下文向量，然后利用NLP中skipGram进行表示学习。

原图以及度序列

在本文中 以下图进行举例

第一跳：与顶点直接相连的顶点集合；第二跳：与顶点隔边相连的顶点集合；第三跳：与顶点隔了三条边的顶点集合
度序列：$s(R_k(i))$ 表示与顶点i相隔k条边的顶点集合内，所有顶点的度组成的有序度序列。

构建多层结构图（multilayer graph）及随机游走

请结合论文详看下图

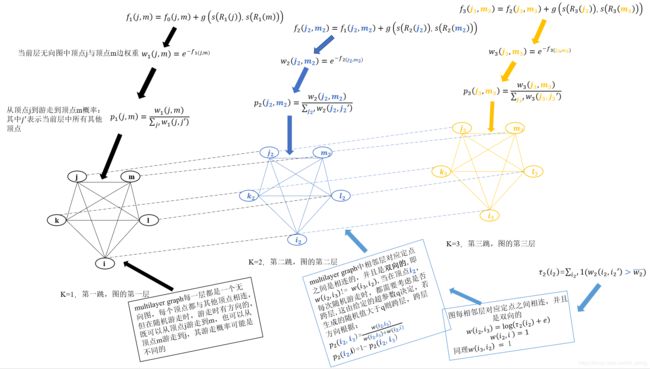
$g(s(R_k(j)),s(R_k(m)))$：表示顶点 $j,m$ 在第k跳的度序列的相似度，论文中采用的是dtw（动态时间规整）方法来衡量两序列的相似度，g 值越大，相似度越小，反之相似度越大。至于dtw如何衡量序列相似度，需要读者自行查看相关资料，这里不详述了。

$w_k(j,m)$：表示 $multilayergraph$ 第k层无向图中，顶点$j$ 与$m$ 边的权重，其权重值由原图中顶点 $j,m$ 在第k跳的度序列的相似度与$f_{k-1}(j,m)$（其中$f_0(j,m)=0$）决定。由此可以构建 $multilayergraph$ 每一层中无向图中两两顶点相连。由上图中可以看出，$f_k$ 是单调不递减的，故$w_k$ 是单调不递增的。

$w(i_k,i_{k+1})、w(i_k,i_{k-1})$： $multilayergraph$ 中相邻层中对应顶点是相连的，如上图中顶点$i、i_2与i_2、i_3$ 都是有边相连，并且这些边是有方向的，即$w(i_2,i_3)!=w(i_3,i_2)$

$p_k(j,m)、p_k(i_2,i_3)$：随机游走的边概率，随机游走概率由边权重决定，边权重越大，选择该边进行游走的概率越大。需要注意的是：每次随机游走时，都需要考虑是否跨层游走，这个由超参数q决定，当生成的随机数大于q，则跨层，反之还留在本层游走。若跨层，还需要考虑向更高层还是更低层跨，这里有：
$$w(i_k,i_{k+1})=log({\tau }_k(i)+e)$$
$${\tau }_k(i)=\sum _{i^{\prime }}1(w_k(i,i^{\prime })>\overline{w_k}$$

若顶点i在第k层的无向图中，与其他顶点的边权重都较大，说明当前层顶点不太适合作为该顶点$i$ 的上下文，应该考虑跳到更高层去找合适的上下文，寻找更高级的上下文特征，因为更高层考虑的视野越大。

由以上规则可由原图构建multilayer graph，并根据边概率进行带权重的随机游走（论文代码里采用alias method，每次对multilayer graph中其他顶点进行游走概率采样，作为下一个要游走的顶点），来学习顶点的潜在表示，显然游走序列中的顶点具有结构相似性，这样即使两顶点即使相距很远，只要结构具有相似性，其学习到的潜在表示也会很类似。

优化

• OPT1：改变 $s(R_k(i))$ 定义方式，例如$s(R_k(i))=(1,1,2,2,2,3,3,4)$，现在定义为：$s(R_k(i))=(1,1,2,2,2,3,3,4)$ 压缩成 $(1,2,2,3,3,2,4,1)$，同时需要变更dtw中计算两定顶点距离计算方式，详情请看论文。
• OPT2：在上面的多层结构图（multilayer graph）中，在每一层中需要计算两两顶点之间的边权重以及游走概率，其实对于structural distance相差很大的两顶点（例如一个顶点度为20，另外一个顶点度为2，当在第一跳时，他们的structural distance就很大了）完全没必要计算，可用二分查找与顶点度相近的顶点，作为multilayer graph中与目标顶点相连的顶点，此时不是所有顶点两两相连；再计算他们之间的边权重，时间复杂度降低到$O(logn)$。
• OPT3：算法总共要计算$k\ast$ 层，很多情况下，网络直径比平均距离要大得多，可以使用一个更小的k，比如平均距离等等来代替这个值。

代码

对于本论文方法，实现代码较为复杂，这里参考的代码为：code，大约花了不到一个下午时间把代码看明白了，下面详细讲下整个代码实现过程。

读图

def load_edgelist(file_, undirected=True):                                                                     
  G = Graph()                                                                                                  
  with open(file_) as f:                                                                                       
    for l in f:                                                                                                
    ┆ if(len(l.strip().split()[:2]) > 1):                                                                      
    ┆   x, y = l.strip().split()[:2]                                                                           
    ┆   x = int(x)                                                                                             
    ┆   y = int(y)                                                                                             
    ┆   G[x].append(y)                                                                                         
    ┆   if undirected:                                                                                         
    ┆   ┆ G[y].append(x)                                                                                       
    ┆ else:                                                                                                    
    ┆   x = l.strip().split()[:2]                                                                              
    ┆   x = int(x[0])                                                                                          
    ┆   G[x] = []                                                                                              
                                                                                                               
  G.make_consistent()  ##返回一个字典，key为顶点，value为原图中与该顶点有边相连的有序顶点列表                                                                                        
  return G

采用OPT1优化，层次遍历寻找每个顶点在不同跳（depth）上的度序列

def getCompactDegreeListsVertices(g,vertices,maxDegree,calcUntilLayer):
    degreeList = {}

    for v in vertices:
    ┆   degreeList[v] = getCompactDegreeLists(g,v,maxDegree,calcUntilLayer)

    return degreeList


def getCompactDegreeLists(g, root, maxDegree,calcUntilLayer):
    #pdb.set_trace()
    t0 = time()

    listas = {}
    vetor_marcacao = [0] * (max(g) + 1)

    # Marcar s e inserir s na fila Q
    queue = deque()
    queue.append(root)
    vetor_marcacao[root] = 1
    l = {}

    ## Variáveis de controle de distância
    depth = 0
    pendingDepthIncrease = 0 ## 用来记录当前顶点depth跳上顶点个数
    timeToDepthIncrease = 1 ## 用来标记当前顶点的depth跳上的顶点集和是否遍历完成

    while queue:
    ┆   vertex = queue.popleft()
    ┆   timeToDepthIncrease -= 1

    ┆   d = len(g[vertex]) ##当前顶点的度
    ┆   if(d not in l):
    ┆   ┆   l[d] = 0
    ┆   l[d] += 1 ## 记录度的频次

    ┆   for v in g[vertex]:
    ┆   ┆   if(vetor_marcacao[v] == 0):
    ┆   ┆   ┆   vetor_marcacao[v] = 1
    ┆   ┆   ┆   queue.append(v)
    ┆   ┆   ┆   pendingDepthIncrease += 1

    ┆   if(timeToDepthIncrease == 0): ## 若depth跳上的顶点遍历完成，则记录该层上度序列

    ┆   ┆   list_d = []
    ┆   ┆   for degree,freq in l.iteritems():
    ┆   ┆   ┆   list_d.append((degree,freq))
    ┆   ┆   list_d.sort(key=lambda x: x[0])
    ┆   ┆   listas[depth] = np.array(list_d,dtype=np.int32)

    ┆   ┆   l = {}

    ┆   ┆   if(calcUntilLayer == depth):
    ┆   ┆   ┆   break

    ┆   ┆   depth += 1
    ┆   ┆   timeToDepthIncrease = pendingDepthIncrease
    ┆   ┆   pendingDepthIncrease = 0


    t1 = time()
    logging.info('BFS vertex {}. Time: {}s'.format(root,(t1-t0)))

    return listas ## 返回该顶点上度序列字典，key为depth，value为元组（度，频次）

采用OPT2优化，二分查找与顶点度相近的顶点

def create_vectors(self):
        logging.info("Creating degree vectors...")
         degrees = {}
         degrees_sorted = set()
         G = self.G
         for v in G.keys():
                 degree = len(G[v])
                 degrees_sorted.add(degree)
                 if(degree not in degrees):
                         degrees[degree] = {}
                         degrees[degree]['vertices'] = deque()
                 degrees[degree]['vertices'].append(v)
         degrees_sorted = np.array(list(degrees_sorted),dtype='int')
         degrees_sorted = np.sort(degrees_sorted)

         l = len(degrees_sorted)
         for index, degree in enumerate(degrees_sorted):
                 if(index > 0):
                         degrees[degree]['before'] = degrees_sorted[index - 1]
                 if(index < (l - 1)):
                         degrees[degree]['after'] = degrees_sorted[index + 1]
         logging.info("Degree vectors created.")
         logging.info("Saving degree vectors...")
         saveVariableOnDisk(degrees,'degrees_vector') 
         ## 存储字典{度数：{对应度数的顶点集合，存在的与之相邻的上一个度数，存在的与之相邻的下一个度数}}，用来为后面的二分查找

二分查找与顶点度邻近的顶点

def verifyDegrees(degrees,degree_v_root,degree_a,degree_b):

    if(degree_b == -1):
    ┆   degree_now = degree_a
    elif(degree_a == -1):
    ┆   degree_now = degree_b
    elif(abs(degree_b - degree_v_root) < abs(degree_a - degree_v_root)):
    ┆   degree_now = degree_b
    else:
    ┆   degree_now = degree_a

    return degree_now

def get_vertices(v,degree_v,degrees,a_vertices):
    a_vertices_selected = 2 * math.log(a_vertices,2)
    #logging.info("Selecionando {} próximos ao vértice {} ...".format(int(a_vertices_selected),v))
    vertices = deque()

    try:
    ┆   c_v = 0

    ┆   for v2 in degrees[degree_v]['vertices']:
    ┆   ┆   if(v != v2):
    ┆   ┆   ┆   vertices.append(v2)
    ┆   ┆   ┆   c_v += 1
    ┆   ┆   ┆   if(c_v > a_vertices_selected):
    ┆   ┆   ┆   ┆   raise StopIteration

    ┆   if('before' not in degrees[degree_v]):
    ┆   ┆   degree_b = -1
    ┆   else:
    ┆   ┆   degree_b = degrees[degree_v]['before']
    ┆   if('after' not in degrees[degree_v]):
    ┆   ┆   degree_a = -1
    ┆   else:
    ┆   ┆   degree_a = degrees[degree_v]['after']
    ┆   if(degree_b == -1 and degree_a == -1):
    ┆   ┆   raise StopIteration
    ┆   degree_now = verifyDegrees(degrees,degree_v,degree_a,degree_b)

    ┆   while True:
    ┆   ┆   for v2 in degrees[degree_now]['vertices']:
    ┆   ┆   ┆   if(v != v2):
    ┆   ┆   ┆   ┆   vertices.append(v2)
    ┆   ┆   ┆   ┆   c_v += 1
    ┆   ┆   ┆   ┆   if(c_v > a_vertices_selected):
    ┆   ┆   ┆   ┆   ┆   raise StopIteration

    ┆   ┆   if(degree_now == degree_b):
    ┆   ┆   ┆   if('before' not in degrees[degree_b]):
    ┆   ┆   ┆   ┆   degree_b = -1
    ┆   ┆   ┆   else:
    ┆   ┆   ┆   ┆   degree_b = degrees[degree_b]['before']
    ┆   ┆   else:
    ┆   ┆   ┆   if('after' not in degrees[degree_a]):
    ┆   ┆   ┆   ┆   degree_a = -1
    ┆   ┆   ┆   else:
    ┆   ┆   ┆   ┆   degree_a = degrees[degree_a]['after']
    ┆   ┆
    ┆   ┆   if(degree_b == -1 and degree_a == -1):
    ┆   ┆   ┆   raise StopIteration
    ┆   ┆   degree_now = verifyDegrees(degrees,degree_v,degree_a,degree_b)

    except StopIteration:
    ┆   #logging.info("Vértice {} - próximos selecionados.".format(v))
    ┆   return list(vertices)

    return list(vertices) ## 返回与顶点v度相近的顶点列表

def splitDegreeList(part,c,G,compactDegree):
    if(compactDegree):
    ┆   logging.info("Recovering compactDegreeList from disk...")
    	# degreeList:字典{顶点：{depth:(度，频次)}} 
    ┆   degreeList = restoreVariableFromDisk('compactDegreeList') 
    else:
    ┆   logging.info("Recovering degreeList from disk...")
    ┆   degreeList = restoreVariableFromDisk('degreeList')

    logging.info("Recovering degree vector from disk...")
    # 字典{度数：{对应度数的顶点集合，存在的与之相邻的上一个度数，存在的与之相邻的下一个度数}}
    degrees = restoreVariableFromDisk('degrees_vector') 

    degreeListsSelected = {}
    vertices = {}
    a_vertices = len(G)

    for v in c:
    ┆   nbs = get_vertices(v,len(G[v]),degrees,a_vertices)
    ┆   vertices[v] = nbs ## 记录与顶点v度相近的顶点列表
    ┆   degreeListsSelected[v] = degreeList[v]
    ┆   for n in nbs:
    ┆   ┆   degreeListsSelected[n] = degreeList[n]
    
	## 存储每个顶点所选定的要计算的顶点集合
    saveVariableOnDisk(vertices,'split-vertices-'+str(part)) 
     ## 存储每个顶点的要计算顶点集合的度序列,用作后面的边权重计算
    saveVariableOnDisk(degreeListsSelected,'split-degreeList-'+str(part))

计算二分查找得到顶点之间的相似度（非边权重和游走概率）

def calc_distances(part, compactDegree = False):

    vertices = restoreVariableFromDisk('split-vertices-'+str(part))
    degreeList = restoreVariableFromDisk('split-degreeList-'+str(part))

    distances = {}

    if compactDegree:
    ┆   dist_func = cost_max
    else:
    ┆   dist_func = cost

    for v1,nbs in vertices.iteritems():
    ┆   lists_v1 = degreeList[v1]

    ┆   for v2 in nbs:
    ┆   ┆   t00 = time()
    ┆   ┆   lists_v2 = degreeList[v2]

    ┆   ┆   max_layer = min(len(lists_v1),len(lists_v2))
    ┆   ┆   distances[v1,v2] = {}

    ┆   ┆   for layer in range(0,max_layer):
    ┆   ┆   ┆   dist, path = fastdtw(lists_v1[layer],lists_v2[layer],radius=1,dist=dist_func)

    ┆   ┆   ┆   distances[v1,v2][layer] = dist

    ┆   ┆   t11 = time()
    ┆   ┆   logging.info('fastDTW between vertices ({}, {}). Time: {}s'.format(v1,v2,(t11-t00)))


    preprocess_consolides_distances(distances)
    ## 存储字典{(顶点1，顶点2)：{第k层layer: 相似度}}
    saveVariableOnDisk(distances,'distances-'+str(part))
    return

构建多层结构图（multilayer graph）

这个有点麻烦，我们一个个的来看怎么实现的

def generate_distances_network_part1(workers):
    parts = workers
    weights_distances = {}
    for part in range(1,parts + 1):
    ┆
    ┆   logging.info('Executing part {}...'.format(part))
     	## 加载字典{(顶点1，顶点2)：{第k层layer: 相似度}}
    ┆   distances = restoreVariableFromDisk('distances-'+str(part))
    ┆
    ┆   for vertices,layers in distances.iteritems():
    ┆   ┆   for layer,distance in layers.iteritems():
    ┆   ┆   ┆   vx = vertices[0]
    ┆   ┆   ┆   vy = vertices[1]
    ┆   ┆   ┆   if(layer not in weights_distances):
    ┆   ┆   ┆   ┆   weights_distances[layer] = {}
    ┆   ┆   ┆   weights_distances[layer][vx,vy] = distance

    ┆   logging.info('Part {} executed.'.format(part))

    for layer,values in weights_distances.iteritems():
    	## 存储每一层的字典{(顶点1，顶点2):相似度}
    ┆   saveVariableOnDisk(values,'weights_distances-layer-'+str(layer))
    return

def generate_distances_network_part2(workers):
    parts = workers
    graphs = {}
    for part in range(1,parts + 1):

    ┆   logging.info('Executing part {}...'.format(part))
    	## 加载字典{(顶点1，顶点2)：{k(第k层layer): 相似度}}
    ┆   distances = restoreVariableFromDisk('distances-'+str(part))

    ┆   for vertices,layers in distances.iteritems():
    ┆   ┆   for layer,distance in layers.iteritems():
    ┆   ┆   ┆   vx = vertices[0]
    ┆   ┆   ┆   vy = vertices[1]
    ┆   ┆   ┆   if(layer not in graphs):
    ┆   ┆   ┆   ┆   graphs[layer] = {}
    ┆   ┆   ┆   if(vx not in graphs[layer]):
    ┆   ┆   ┆   ┆  graphs[layer][vx] = []
    ┆   ┆   ┆   if(vy not in graphs[layer]):
    ┆   ┆   ┆   ┆  graphs[layer][vy] = []
    ┆   ┆   ┆   graphs[layer][vx].append(vy)
    ┆   ┆   ┆   graphs[layer][vy].append(vx)
    ┆   logging.info('Part {} executed.'.format(part))

    for layer,values in graphs.iteritems():
    	## 存储每一层中：字典{该层顶点：需要计算的顶点列表}
    ┆   saveVariableOnDisk(values,'graphs-layer-'+str(layer))

    return

计算所有层所有边的游走概率，并构建alias method中的Alias Table

def generate_distances_network_part3():

    layer = 0
    while(isPickle('graphs-layer-'+str(layer))):
    	## 加载每一层中：字典{k(第k层layer):{顶点：需要计算的顶点列表}}
    ┆   graphs = restoreVariableFromDisk('graphs-layer-'+str(layer))
    	## 加载每一层的字典{(顶点1，顶点2):相似度}
    ┆   weights_distances = restoreVariableFromDisk('weights_distances-layer-'+str(layer))

    ┆   logging.info('Executing layer {}...'.format(layer))
    ┆   alias_method_j = {}
    ┆   alias_method_q = {}
    ┆   weights = {}

    ┆   for v,neighbors in graphs.iteritems():
    ┆   ┆   e_list = deque()
    ┆   ┆   sum_w = 0.0

    ┆   ┆   for n in neighbors:
    ┆   ┆   ┆   if (v,n) in weights_distances:
    ┆   ┆   ┆   ┆   wd = weights_distances[v,n]
    ┆   ┆   ┆   else:
    ┆   ┆   ┆   ┆   wd = weights_distances[n,v]
    ┆   ┆   ┆   w = np.exp(-float(wd))
    ┆   ┆   ┆   e_list.append(w)
    ┆   ┆   ┆   sum_w += w

    ┆   ┆   e_list = [x / sum_w for x in e_list]
    ┆   ┆   weights[v] = e_list ## 计算游走概率
    ┆   ┆   J, q = alias_setup(e_list) ## 构建Alias Table
    ┆   ┆   alias_method_j[v] = J
    ┆   ┆   alias_method_q[v] = q

		## 存储每一层的：字典{顶点：与该顶点相连的所有边的游走概率}
    ┆   saveVariableOnDisk(weights,'distances_nets_weights-layer-'+str(layer))
    	## 存储每一层的Alias Table的alias
    ┆   saveVariableOnDisk(alias_method_j,'alias_method_j-layer-'+str(layer))
    	## 存储每一层的Alias Table的prob
    ┆   saveVariableOnDisk(alias_method_q,'alias_method_q-layer-'+str(layer))
    ┆   logging.info('Layer {} executed.'.format(layer))
    ┆   layer += 1

    logging.info('Weights created.')

    return

alias method，可以参考https://blog.csdn.net/haolexiao/article/details/65157026，理解下代码

def alias_setup(probs):
    '''
    Compute utility lists for non-uniform sampling from discrete distributions.
    Refer to https://hips.seas.harvard.edu/blog/2013/03/03/the-alias-method-efficient-sampling-with-many-discrete-outcomes/
    for details
    '''
    K = len(probs)
    q = np.zeros(K)
    J = np.zeros(K, dtype=np.int)

    smaller = []
    larger = []
    for kk, prob in enumerate(probs):
    ┆   q[kk] = K*prob
    ┆   if q[kk] < 1.0:
    ┆   ┆   smaller.append(kk)
    ┆   else:
    ┆   ┆   larger.append(kk)

    while len(smaller) > 0 and len(larger) > 0:
    ┆   small = smaller.pop()
    ┆   large = larger.pop()

    ┆   J[small] = large ## 小列的别名
    ┆   q[large] = q[large] + q[small] - 1.0 ## 将大的列填满小的列，同时记录prob，当在采样时大于该prob取alias
    ┆   if q[large] < 1.0:
    ┆   ┆   smaller.append(large)
    ┆   else:
    ┆   ┆   larger.append(large)

    return J, q

def generate_distances_network_part4():
    logging.info('Consolidating graphs...')
    graphs_c = {}
    layer = 0
    while(isPickle('graphs-layer-'+str(layer))):
    ┆   logging.info('Executing layer {}...'.format(layer))
    	## 加载每一层中：字典{该层顶点：需要计算的顶点列表}
    ┆   graphs = restoreVariableFromDisk('graphs-layer-'+str(layer))
    ┆   graphs_c[layer] = graphs
    ┆   logging.info('Layer {} executed.'.format(layer))
    ┆   layer += 1


    logging.info("Saving distancesNets on disk...")
    ## 存储字典{layer:{该层顶点：需要计算的顶点列表}}
    saveVariableOnDisk(graphs_c,'distances_nets_graphs')
    logging.info('Graphs consolidated.')
    return

def generate_distances_network_part5():
    alias_method_j_c = {}
    layer = 0
    while(isPickle('alias_method_j-layer-'+str(layer))):
    ┆   logging.info('Executing layer {}...'.format(layer))
    ┆   alias_method_j = restoreVariableFromDisk('alias_method_j-layer-'+str(layer))
    ┆   alias_method_j_c[layer] = alias_method_j
    ┆   logging.info('Layer {} executed.'.format(layer))
    ┆   layer += 1

    logging.info("Saving nets_weights_alias_method_j on disk...")
    saveVariableOnDisk(alias_method_j_c,'nets_weights_alias_method_j')

    return

def generate_distances_network_part6():
    alias_method_q_c = {}
    layer = 0
    while(isPickle('alias_method_q-layer-'+str(layer))):
    ┆   logging.info('Executing layer {}...'.format(layer))
    ┆   alias_method_q = restoreVariableFromDisk('alias_method_q-layer-'+str(layer))
    ┆   alias_method_q_c[layer] = alias_method_q
    ┆   logging.info('Layer {} executed.'.format(layer))
    ┆   layer += 1

    logging.info("Saving nets_weights_alias_method_q on disk...")
    saveVariableOnDisk(alias_method_q_c,'nets_weights_alias_method_q')

    return

随机游走

def generate_parameters_random_walk(workers):

    logging.info('Loading distances_nets from disk...')

    sum_weights = {}
    amount_edges = {}

    layer = 0
    while(isPickle('distances_nets_weights-layer-'+str(layer))):
    ┆   logging.info('Executing layer {}...'.format(layer))
    	## 加载每一层的：字典{顶点：与该顶点相连的所有边的游走概率}
    ┆   weights = restoreVariableFromDisk('distances_nets_weights-layer-'+str(layer))

    ┆   for k,list_weights in weights.iteritems():
    ┆   ┆   if(layer not in sum_weights):
    ┆   ┆   ┆   sum_weights[layer] = 0
    ┆   ┆   if(layer not in amount_edges):
    ┆   ┆   ┆   amount_edges[layer] = 0

    ┆   ┆   for w in list_weights:
    ┆   ┆   ┆   sum_weights[layer] += w ##记录当前层顶点权重和
    ┆   ┆   ┆   amount_edges[layer] += 1 ## 记录当前层边的数量
    ┆
    ┆   logging.info('Layer {} executed.'.format(layer))
    ┆   layer += 1

    average_weight = {}
    for layer in sum_weights.keys():
    ┆   average_weight[layer] = sum_weights[layer] / amount_edges[layer] ## 当前层的平均权重

    logging.info("Saving average_weights on disk...")
    ## 存储每一层的平均权重
    saveVariableOnDisk(average_weight,'average_weight')

    amount_neighbours = {}

    layer = 0
    while(isPickle('distances_nets_weights-layer-'+str(layer))):
    ┆   logging.info('Executing layer {}...'.format(layer))
    	## 加载每一层的：字典{顶点：与该顶点相连的所有边的游走概率}
    ┆   weights = restoreVariableFromDisk('distances_nets_weights-layer-'+str(layer))

    ┆   amount_neighbours[layer] = {}

    ┆   for k,list_weights in weights.iteritems():
    ┆   ┆   cont_neighbours = 0
    ┆   ┆   for w in list_weights:
    ┆   ┆   ┆   if(w > average_weight[layer]):
    ┆   ┆   ┆   ┆   cont_neighbours += 1
    ┆   ┆   amount_neighbours[layer][k] = cont_neighbours

    ┆   logging.info('Layer {} executed.'.format(layer))
    ┆   layer += 1

    logging.info("Saving amount_neighbours on disk...")
    ## 存储字典{layer:{顶点：Γk(顶点)}}
    saveVariableOnDisk(amount_neighbours,'amount_neighbours')

alias按概率采样，作为随机游走的下个顶点

def alias_draw(J, q):
    '''
    Draw sample from a non-uniform discrete distribution using alias sampling.
    '''
    K = len(J) 
    
    kk = int(np.floor(np.random.rand()*K))
    if np.random.rand() < q[kk]:
    ┆   return kk
    else:   
    ┆   return J[kk]

def chooseNeighbor(v,graphs,alias_method_j,alias_method_q,layer):
    v_list = graphs[layer][v]

    idx = alias_draw(alias_method_j[layer][v],alias_method_q[layer][v])
    v = v_list[idx]

    return v

def exec_random_walk(graphs,alias_method_j,alias_method_q,v,walk_length,amount_neighbours):
    original_v = v ## 游走的起点
    t0 = time()
    initialLayer = 0
    layer = initialLayer


    path = deque()
    path.append(v)

    while len(path) < walk_length:
    ┆   r = random.random()

    ┆   if(r < 0.3): ## 在当前层游走，这个0.3就是上面说的超参数q
    ┆   ┆   ┆   v = chooseNeighbor(v,graphs,alias_method_j,alias_method_q,layer)
    ┆   ┆   ┆   path.append(v)

    ┆   else: ## 跨层游走
    ┆   ┆   r = random.random()
    ┆   ┆   limiar_moveup = prob_moveup(amount_neighbours[layer][v])
    ┆   ┆   if(r > limiar_moveup): ## 往低层游走
    ┆   ┆   ┆   if(layer > initialLayer):
    ┆   ┆   ┆   ┆   layer = layer - 1
    ┆   ┆   else: ## 往高层游走
    ┆   ┆   ┆   if((layer + 1) in graphs and v in graphs[layer + 1]):
    ┆   ┆   ┆   ┆   layer = layer + 1

    t1 = time()
    logging.info('RW - vertex {}. Time : {}s'.format(original_v,(t1-t0)))
	
    return path ## 以顶点v为起点，游走的路径

def exec_ramdom_walks_for_chunck(vertices,graphs,alias_method_j,alias_method_q,walk_length,amount_neighbours):
    walks = deque()
    for v in vertices:
    ┆   walks.append(exec_random_walk(graphs,alias_method_j,alias_method_q,v,walk_length,amount_neighbours))
    return walks ## 所有顶点为起点的游走路径

skipGram学习表示

def learn_embeddings():
        '''
        Learn embeddings by optimizing the Skipgram objective using SGD.
        '''
        logging.info("Initializing creation of the representations...")
        walks = LineSentence('random_walks.txt')
        model = Word2Vec(walks, size=args.dimensions, window=args.window_size, min_count=0, hs=1, sg=1, workers=args.workers, iter=args.iter)
        model.wv.save_word2vec_format(args.output)
        logging.info("Representations created.")

        return

实验

略

个人总结

• 论文中提出的学习顶点的structural identity，和顶点之间的structural similarity，没有利用任何顶点的位置信息，和一些距离特征，完全由顶点k跳的度序列来学习这种结构相似性，这样避免了距离很远的结构相似顶点却学不到相似的潜在表达，论文中关于构造多层结构图，边权重、随机游走概率、度序列相似度等过程很有意思，论文实验结果也证明了其有效性。
• 相比Deepwalk、Line等图表示方面的论文，该论文稍微有点难读，而本文的介绍较为精炼，如读者有疑惑建议可以看看【论文笔记】struc2vec，写的很详细。

参考

• https://arxiv.org/pdf/1704.03165.pdf
• https://zhuanlan.zhihu.com/p/63175042 (写的很细，推荐看看）
• https://github.com/leoribeiro/struc2vec
• https://blog.csdn.net/haolexiao/article/details/65157026