分布式哈希表与Kademlia算法

在我们总结分布式哈希表之前不妨让我们先来回想一下，什么是哈希？下面是wikipedia的定义：

散列（英语：Hashing）是计算机科学中一种对数据的处理方法，通过某种特定的函数/算法（称为散列函数/算法）将要检索的项与用来检索的索引（称为散列，或者散列值）关联起来，生成一种便于搜索的数据结构（称为散列表）。旧译哈希（误以为是人名而采用了音译）。它也常用作一种信息安全的实现方法，由一串数据中经过散列算法（Hashing algorithms）计算出来的数据指纹（data fingerprint），经常用来识别文件与数据是否有被窜改，以保证文件与数据确实是由原创者所提供。

很多语言的内置数据结构像Python中的dict，Java中的HashMap，都是基于哈希表的实现。但是大多数语言的哈希表实现中哈希表的数据都是需要存放在同一台机器中的内存。如果哈希表的数据量巨大，一台机器的内存根本放不下怎么办呢？

分布式哈希表

分布式哈希表对应的英文名称是Distributed Hash Table，简称DHT。分布式哈希表在概念上类似于传统的哈希表，差异在于：

• 传统的哈希表主要用于单机上的某个软件中；
• 分布式哈希表主要用于分布式系统，用于来存储大量甚至是海量的数据。
  
  如下是Wikipedia中分布式哈希表的定义：

A distributed hash table (DHT) is a class of a decentralized distributed system that provides a lookup service similar to a hash table: (key, value) pairs are stored in a DHT, and any participating node can efficiently retrieve the value associated with a given key. Keys are unique identifiers which map to particular values, which in turn can be anything from addresses, to documents, to arbitrary data.[1] Responsibility for maintaining the mapping from keys to values is distributed among the nodes, in such a way that a change in the set of participants causes a minimal amount of disruption. This allows a DHT to scale to extremely large numbers of nodes and to handle continual node arrivals, departures, and failures.

说的简单一点，分布式哈希表就是把哈希表存储在多个节点上，每个节点存储一部分的文件，和路由信息，从而实现整个系统的寻址和存储功能，并且能容忍新增节点、删除节点以及节点故障的分布式哈希表系统（当然这个分布式哈希表系统也能实现根据key查找对应value的基本功能）。

为什么会出现分布式哈希表？

在P2P文件共享的发展史上，出现过3种不同技术路线（三代）。

第一代

采用中央服务器的模式——每个结点都需要先连接到中央服务器，然后才能查找自己想要的文件在哪里。这种技术最大的缺点是中央服务器成为整个P2P网络的单点故障。这种P2P的典型代表是Napster。

第二代

由于第一代的单点故障，第二代P2P在查找文件的时候，修改为向和自己相连的所有节点进行询问；被询问的节点如果不知道这个文件在哪里，就再次进行广播……如此反复，知道找到所需文件。显而易见这种技术的最大缺点就是广播风暴，并且严重占用了网络带宽，也会严重消耗节点的系统资源。即使在协议层通过设置TTL（Time To Live），限制查询过程只递归N轮，依然无法彻底解决此弊端。因为这种方法太吓人，获得了Query Flooding的绰号。这类P2P的典型代表是Gnutella的早期版本。

第三代

第三代就是今天要讨论的分布式哈希表。通过分布式哈希表，不但避免了单点故障也避免了广播风暴。

分布式哈希表有哪些应用场景？

分布式哈希表目前被广泛应用于分布式系统中，比如：

• 分布式文件系统
• 分布式缓存
• 区块链
• 无中心的聊天工具/IM（比如:TOX）

Kademlia（Kad）算法

注意：由于“Kademlia”这个词太长，所以很多资料上该算法采用“Kad”这个简写。

分布式哈希表有需要实现方案，这里我为大家总结一下常见一种算法Kademlia。Kademlia算法是一种分布式存储及路由的算法。试想一下，一所10000人的学校，现在学校决定拆除图书馆（不设立中央服务器，即去中心化），将图书馆里的所有的书都分发到每位学生手里（所有的分拣分散存储在各个节点上）。即所有的学生共同组成一个分布式的图书馆。

在这种场景下，有几个关键问题需要回答：

1. 每个同学手上都分配那些书？学校新购买的图书又如何分配？即如何分配存储内容（文件）到各个节点，新增或者删除内容（文件）如何处理；
2. 学校有10000人，每个学生可能只认识学校里的一部分人，那么当你需要查找例如《算法导论》的时候如何知道哪位同学手上有这本书呢（对全校同学一个一个问一遍，“你有没有《算法导论》？”，这很明显是个不经济的做法）？又如何联系这位同学呢？即一个节点只知道整个系统中一部分节点存储的文件和地址，那么在某一个节点如何获取某个特定的文件，如何找到存储该特定文件的节点的IP与port。
3. 如果手上有《算法导论》的同学某天请假了，那是不是这本书就找不到了？即如果某个结点故障或者下线了，那是不是会导致改节点上存储的文件了？

节点的要素

接下来，让我来看看Kademlia算法是如何巧妙的解决这些问题的。
首先我们来看看每个同学（节点）都有哪些属性：

• 学号（NodeId，2进制，160位）
• 手机号码（节点IP地址及端口）

每个同学都会维护一下内容：

• 从图书馆发下来的书本（被分配需要存储的内容（文件）），每本书当然都有书名和书本内容（内容以对的形式存储，可以理解为文件名和文件内容）；
• 一个通讯录，包含一小部分其他同学的学号和手机号，通讯录按照学号分层（这个通讯录就是一个路由表，称为k-bucket，按照NodeId分层，记录有限个数的其他节点的Id和IP地址及端口，这里暂时不需要完全理解这个路由表，后面会详细说明）。

根据上面那个类比，可以得出一下表格：

关于为什么不是每个同学都有全量通讯录（每个节点维护全量路由信息）：其一，分布式系统中节点的进入和退出时相当频繁的，每次有变动时都全网广播通讯录更新，通讯录会很大；其二，一旦一个同学被坏人绑架了（节点被黑客攻破），则坏人马上就拥有了所有人的手机号码，这并不安全。其三，分布式系统中的节点可能会数量巨大，如果维护全量通讯录会使的通讯录巨大。

文件的存储及查找

原来收藏在图书馆里的图书，以一种什么样的方式分发到同学们的手里呢？大致的原则是：1. 书本能够比较均匀的分布式在同学们的手里，不会出现部分同学手机书籍特别多，而部分同学连一本书都没有的情况；2. 同学想找一本特定的书的时候能够以一种相对比较简单的方式找到这本书。
Kademlia算法做了下面这种安排：
假设《算法导论》这本书的书名hash值是00010000，那么这本书就会被要求存在学号为00010000的同学手上（这要求hash算法的值域和NodeId的值域一致，即要求书名在经过hash之后存在对应的NodeId。当然此处仅仅是进行假设，实际场景中，应该是文件数量大大高于节点数量，所以更多的场合时，文件上传是找不到命名完全一致的节点，然后就去找异或距离最近的节点进行存储。）。还需要考虑到会有同学缺勤。万一00010000今天没有来上学（节点没有上线或者彻底退出网络），那《算法导论》这本书岂不是谁都看不到了？所以算法要求这本书不能只存在一个同学手上，而是被要求同时存储在学号最相近00010000的k位同学手上，即00010001、00010010、00010011……等同学手上都会有这本书。同样的，当你需要找《算法导论》这本书的时候，将书名hash一下，得到00010000，你就知道该找那几位同学了。剩下的问题，就是找到这几位同学的手机号码。

节点的异或距离

由于你手上只有一部分同学的通讯录，你很可能并没有00010000的手机号码（IP地址）。那如何联系上该位同学呢？一个可行的思路就是在你的通讯录找到一个拥有这位同学的手机号码的同学。算法的设计是，如果一个同学的学号前几位数字相同的越多，则你们在同班的可能性越大，你手上的通讯录里存有他的手机号码的概率就越大。算法的核心思路就是：当你知道目标同学Z与你之间的距离，你可以在你的通讯录上先找到一个你认为与同学Z最相近的同学B，请同学B再进一步去查找同学Z的手机号码。

在Kademlia算法中，距离是学号（NodeId）之间的异或距离（xor distance）。异或是针对二进制的运算。如下是百度百科中异或操作的解释：

异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1）

举两个例子：
01010000和01010010距离是00000010，也就是2。；
0100000与00000001距离是01000001，也就是65；
如此类推。

那路由表是如何按距离分层的呢？按异或距离分层，基本上可以理解为按位数分层。设想一下情景：
以00000110为基础节点，如果一个节点的NodeId，前面所有位数都与它相同，只有最后1位不同，这样的节点只有一个——00000111，与基础节点的异或值为00000001，即距离为1；对于00000110而言，这样的节点归为k-bucket 1；
如果一个节点的NodeId，前面的所有位数相同，从倒数第二位开始不同，这样的节点只有2个：00000101、00000100，与基础节点的异或值为00000011和00000010，即距离范围为3和2；对于00000110而言，这样的节点归为k-bucket 2；
……
如果一个节点的NodeId，前面所有的位数相同，从倒数第N位开始不同，这样的节点只有2^(i-1)个，与基础节点的距离范围[2^(i-1)，2ⁱ);对于000000110而言，这样的节点归为k-bucket i；

对上面描述的另外一种理解方式：如果将整个网络的节点梳理为一个按照节点NodeId排列的二叉树，树最末端的每个叶子便是一个节点，则下图就比较直观的展现出，节点之间的距离关系。

上图中，右下角的黑色实心圆是基础节点00000110。

回到我们的类比，每个同学只维护了一部分的通讯录，这个通讯录按照距离分层（可以理解为按照序号与自己学号从第几位开始不同而分层），即k-bucket 1，k-bucket 2，k-bucket 3……虽然每个k-bucket中实际存在的同学人数在逐渐增多，但每个同学在他自己的每个k-bucket中只记录k位同学的手机号码（k个节点的地址与端口，这里的k是一个可调节的常量参数）。
默认情况下Kademlia算法的节点NodeId有160位，所以每个同学的通讯录共分160层（节点共有160个k-bucket）。整个网络最多可以容纳2^160个同学（节点），但是每个同学（节点）最多只维护160*k行通讯录（其他节点的地址与端口）。

节点定位

我们现在来阐述一下完整的找书的流程。
A同学（学号00000110）先找《算法导论》，A首先需要计算书名的哈希值，hash（《算法导论》）=00010000.那么A就知道他需要找到00010000（命名为Z同学）或者学号与Z相邻的同学。
Z的学号00010000与自己的额激活距离是00010110，距离范围在[2⁴，2⁵)，所以这个Z同学可能在k-bucket 5中（或者说，Z同学的学号与A同学的学号从第5位开始不同，所以Z同学可能在k-bucket 5中）。
然后A同学看看自己的k-bucket 5有没有Z同学：

• 如果有，那就直接联系Z同学要书；
• 如果没有，在k-bucket 5里随便找一个B同学（注意任意B同学，他的学号第5位肯定与Z相同，即它与Z同学的距离会小于2⁴相当于比Z、A之间的距离缩短了一半以上），请求B同学在它自己的通讯录里按同样的搜索方法，可以在自己的通讯录里找到一个离Z更近的C同学（Z与C之间距离小于2³），把C同学推荐给A；A同学请求C同学进行下一步查找。
  
  Kademlia的这种查询机制，优点像是将一张纸不断的对折来收缩搜索范围，保证对于任意N个学生，最多只需要查询log₂(N)次，即可找到获取目标同学的联系方式（即在对于任意一个[2_(n-1)，2_n)节点的网络，做多只需要N步就可以找到目标节点）。
  
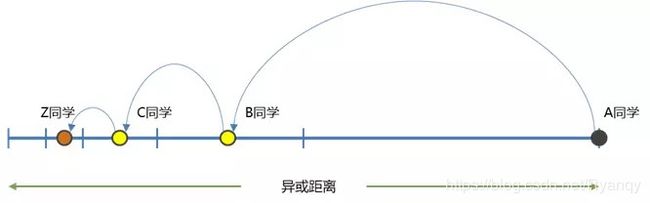
  以上便是Kademlia算法的基本原理。

Kademlia算法的三个参数：keyspace，k和α

• keyspace
  即NodeId有多少位，默认是160位，决定每个节点通讯录有几层。
• k
  每一层k-bucket里装k个node的信息，每次查找node的时候，返回k个node的信息，对于某个特定的data，离key最近的k个节点都会要求存储这个data，默认k的值是8
• α
  每次向其他node请求查询某个node时，会向α个node发出请求。

参考：
聊聊分布式散列表（DHT）的原理——以 Kademlia（Kad） 和 Chord 为例
易懂分布式 | Kademlia算法
Kademlia: A Peer-to-peer information system based on the XOR Metric