matlab实现RSSI定位

一、要求

要求一：RSSI的测量值由对数路径损耗模型产生，为减小波动造成的误差，其值可由多次测量取平均值来得到。

要求二：对数路径损耗模型中的参考距离路径损耗和路径损耗因子可通过参考点相互之间的测量值估计。

要求三：完成理想情况下（参考距离路径损耗和路径损耗因子已知）与实际情况下的RMSE曲线对比图，横坐标为噪声方差，纵坐标为RMSE。

二、设计

1.RSSI定位原理
利用已知发射信号强度和接收节点收到的信号强度，计算在传输过程的损耗，使用信号模型将损耗转化为待定位目标与已知节点之间的距离。

Pd=Pd0-10nlg(d/d0)+ξ

2.采用最小二乘法，估计路径损耗，接收功率里面的两个位置参数

3.采用TOALLOP算法计算未知节点坐标

三、代码

TOALLOP：

function theta=TOALLOP(A,p,j)
[m,~]=size(A);  
k=sum(A.^2,2);
k1=k([1:j-1,j+1:m],:); %取出J行
A1=A([1:j-1,j+1:m],:); %取出J行
A2=A1-ones(m-1,1)*A(j,:); 
p1=p([1:j-1,j+1:m],:); %取出J行
p2=p(j).^2*ones(m-1,1)-p1.^2-(k(j)*ones(m-1,1)-k1); 
theta=1/2*inv(A2'*A2)*A2'*p2; %利用最小二乘解，得
theta=theta';%转换为（x,y）形式

parameter_est：

function [pd0_est,n_est]=parameter_est(A,sigma) 
[m,~]=size(A); 
pd0=0;
n=3; 
d=zeros(m,m); 
tt=5; 
sigma1=10^(sigma/10); 
h1=[];
G1=[]; 
for i=1:m 
    for j=1:m 
        if i~=j 
           d(i,j)=norm(A(i,:)-A(j,:));
           for k=1:tt 
               prd(k)=pd0-10*n*log10(d(i,j))-sigma1*randn; 
           end 
           RSSI=mean(prd);
           d_distance=-10*log10(d(i,j)); 
           h1=[h1;RSSI];
           G1=[G1;d_distance]; 
        end
     end
end
h=h1;
[m1,~]=size(h); 
G=[ones(m1,1),G1];
x=inv(G'*G)*G'*h; 
pd0_est=x(1,1);
n_est=x(2,1);
end

主函数：

clear all; 
clc; 
BS1=[0,0];
BS2=[500,0];
BS3=[500,500];
BS4=[0,500]; 
MS=[100,100]; 
std_var=[0,2,4,6]; 
A=[BS1;BS2;BS3;BS4]; 
number=300; 
pd0=0;
n=3; 
tt=20; 
% the number of RSSI measurement for each BS
for j=1:length(std_var)
    error1=0;
    error2=0; 
    std_var1=std_var(j); 
    for i=1:number 
        r1=A-ones(4,1)*MS; 
        r2=(sum(r1.^2,2)).^(1/2); 
        for k=1:tt 
            rssi(:,k)=pd0-10*n*log10(r2)-10^(std_var1/10)*randn(4,1); 
        end 
        RSSI1=mean(rssi,2);
        % ideal situation 
        r1=10.^((RSSI1-pd0)/(-10*n)); 
        % real situation 
        [p_est,n_est]=parameter_est(A,std_var1); 
        r2=10.^((RSSI1-p_est)/(-10*n_est)); 
        theta1=TOALLOP(A,r1,1); 
        theta2=TOALLOP(A,r2,1); 
        error1=error1+norm(MS-theta1)^2; 
        error2=error2+norm(MS-theta2)^2; 
    end 
    RMSE1(j)=(error1/number)^(1/2); 
    RMSE2(j)=(error2/number)^(1/2); 
end
% plot 
plot(std_var,RMSE1,'-O',std_var,RMSE2,'-s') 
xlabel('The standard deviation of RSS measurement (db)'); 
ylabel('RMSE'); 
legend('Ideal','Real');

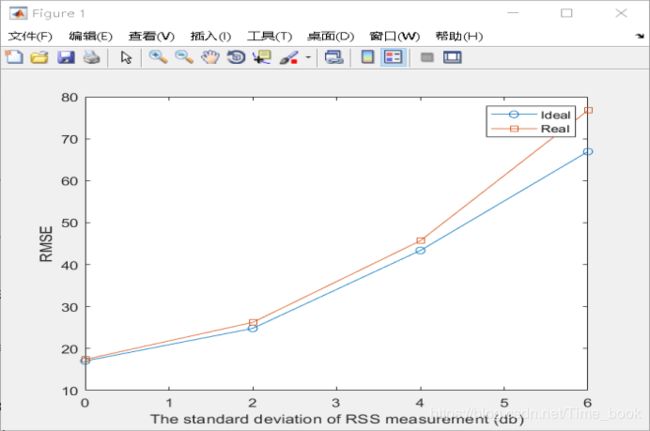
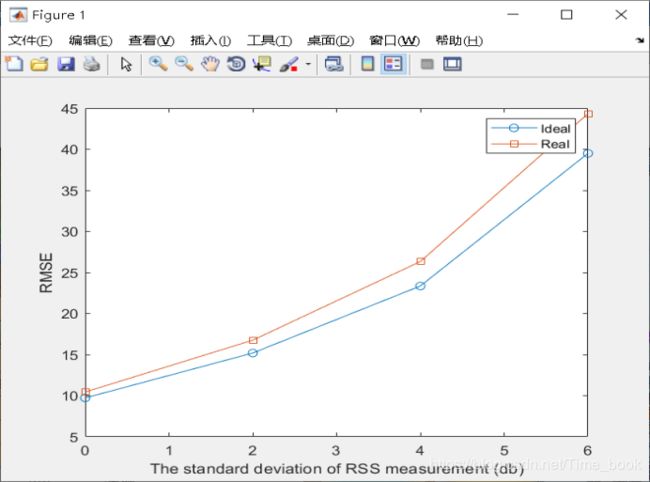
四、结果

tt=5

tt=10

tt=15

五、结论

由上图所示，横坐标表示的RSSI的标准偏差、纵坐标表示的是均方根误差。蓝色表示的是理想情况，红色代表的是实际情况。
1.当RSSI较小时，理想情况与实际情况的RMSE相差不大，近似一致。2.随着RSSI的增大，理想情况与实际情况开始出现差距，并且差距开始变大。
3.随着tt（锚节点的个数）的增加，在RSSI一定的情况下，理想情况与实际情况的RMSE值均减小，也就是说，随着锚节点的个数的增加，定位精度也随之增加。