deeplearning.ai课程作业：Recurrent Neural Networks- Course 5 Week1

deeplearning.ai课程作业：Recurrent Neural Networks- Course 5 Week1

---

需要的依赖文件可以点击这里下载 ，三个部分所需的依赖包都在里面，保存路径的方法可以查看本人头几篇deeplearning.ai的博文，里面有详细说明。

---

Part 1

Building your Recurrent Neural Network - Step by Step

Welcome to Course 5’s first assignment! In this assignment, you will implement your first Recurrent Neural Network in numpy.

Recurrent Neural Networks (RNN) are very effective for Natural Language Processing and other sequence tasks because they have “memory”. They can read inputs $x^{⟨t⟩}$ (such as words) one at a time, and remember some information/context through the hidden layer activations that get passed from one time-step to the next. This allows a uni-directional RNN to take information from the past to process later inputs. A bidirection RNN can take context from both the past and the future.

Notation:

• Superscript $[l]$ denotes an object associated with the $l^{th}$ layer.

  • Example: $a^{[4]}$ is the $4^{th}$ layer activation. $W^{[5]}$ and $b^{[5]}$ are the $5^{th}$ layer parameters.

• Superscript $(i)$ denotes an object associated with the $i^{th}$ example.

  • Example: $x^{(i)}$ is the $i^{th}$ training example input.

• Superscript $⟨t⟩$ denotes an object at the $t^{th}$ time-step.

  • Example: $x^{⟨t⟩}$ is the input x at the $t^{th}$ time-step. $x^{(i)⟨t⟩}$ is the input at the $t^{th}$ timestep of example $i$.

• Lowerscript $i$ denotes the $i^{th}$ entry of a vector.

  • Example: $a_i^{[l]}$ denotes the $i^{th}$ entry of the activations in layer $l$.

We assume that you are already familiar with numpy and/or have completed the previous courses of the specialization. Let’s get started!

Let’s first import all the packages that you will need during this assignment.

import numpy as np
from rnn_utils import *

1 - Forward propagation for the basic Recurrent Neural Network

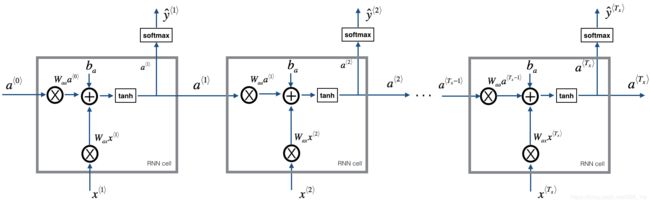
Later this week, you will generate music using an RNN. The basic RNN that you will implement has the structure below. In this example, $T_x=T_y$.

Figure 1: Basic RNN model

Here’s how you can implement an RNN:

Steps:

1. Implement the calculations needed for one time-step of the RNN.
2. Implement a loop over $T_x$ time-steps in order to process all the inputs, one at a time.

Let’s go!

1.1 - RNN cell

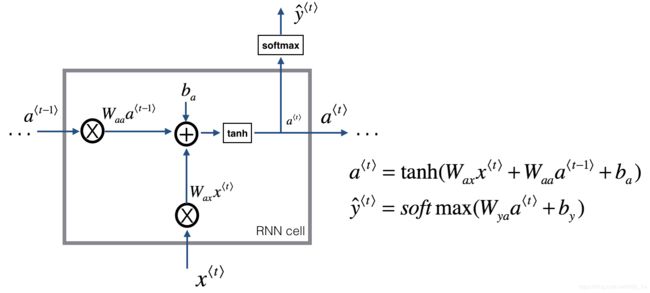
A Recurrent neural network can be seen as the repetition of a single cell. You are first going to implement the computations for a single time-step. The following figure describes the operations for a single time-step of an RNN cell.

Figure 2: Basic RNN cell. Takes as input $x^{⟨t⟩}$ (current input) and $a^{⟨t-1⟩}$ (previous hidden state containing information from the past), and outputs $a^{⟨t⟩}$ which is given to the next RNN cell and also used to predict $y^{⟨t⟩}$

Exercise: Implement the RNN-cell described in Figure (2).

Instructions:

1. Compute the hidden state with tanh activation: $a^{⟨t⟩}=\tanh (W_{aa}{a}^{⟨t-1⟩}+W_{ax}{x}^{⟨t⟩}+b_a)$.
2. Using your new hidden state $a^{⟨t⟩}$, compute the prediction ${\hat{y}}^{⟨t⟩}=softmax(W_{ya}{a}^{⟨t⟩}+b_y)$. We provided you a function: softmax.
3. Store $(a^{⟨t⟩},a^{⟨t-1⟩},x^{⟨t⟩},parameters)$ in cache
4. Return $a^{⟨t⟩}$ , $y^{⟨t⟩}$ and cache

We will vectorize over $m$ examples. Thus, $x^{⟨t⟩}$ will have dimension $(n_x,m)$, and $a^{⟨t⟩}$ will have dimension $(n_a,m)$.

# GRADED FUNCTION: rnn_cell_forward

def rnn_cell_forward(xt, a_prev, parameters):
    """
    Implements a single forward step of the RNN-cell as described in Figure (2)

    Arguments:
    xt -- your input data at timestep "t", numpy array of shape (n_x, m).
    a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
    parameters -- python dictionary containing:
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        ba --  Bias, numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
    Returns:
    a_next -- next hidden state, of shape (n_a, m)
    yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
    cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
    """
    
    # Retrieve parameters from "parameters"
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]
    
    ### START CODE HERE ### (≈2 lines)
    # compute next activation state using the formula given above
    a_next = np.tanh(np.dot(Waa,a_prev)+np.dot(Wax,xt)+ba)
    # compute output of the current cell using the formula given above
    yt_pred = softmax(np.dot(Wya,a_next)+by)   
    ### END CODE HERE ###
    
    # store values you need for backward propagation in cache
    cache = (a_next, a_prev, xt, parameters)
    
    return a_next, yt_pred, cache

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}

a_next, yt_pred, cache = rnn_cell_forward(xt, a_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", a_next.shape)
print("yt_pred[1] =", yt_pred[1])
print("yt_pred.shape = ", yt_pred.shape)

a_next[4] =  [ 0.59584544  0.18141802  0.61311866  0.99808218  0.85016201  0.99980978
 -0.18887155  0.99815551  0.6531151   0.82872037]
a_next.shape =  (5, 10)
yt_pred[1] = [ 0.9888161   0.01682021  0.21140899  0.36817467  0.98988387  0.88945212
  0.36920224  0.9966312   0.9982559   0.17746526]
yt_pred.shape =  (2, 10)

Expected Output:

a_next[4]:	[ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978 -0.18887155 0.99815551 0.6531151 0.82872037]
a_next.shape:	(5, 10)
yt[1]:	[ 0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212 0.36920224 0.9966312 0.9982559 0.17746526]
yt.shape:	(2, 10)

1.2 - RNN forward pass

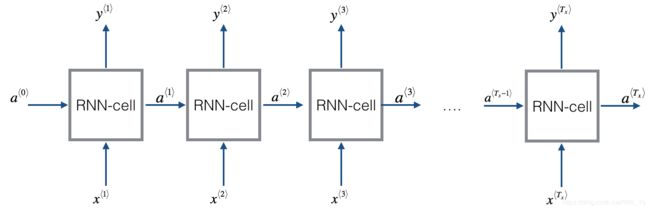
You can see an RNN as the repetition of the cell you’ve just built. If your input sequence of data is carried over 10 time steps, then you will copy the RNN cell 10 times. Each cell takes as input the hidden state from the previous cell ($a^{⟨t-1⟩}$) and the current time-step’s input data ($x^{⟨t⟩}$). It outputs a hidden state ($a^{⟨t⟩}$) and a prediction ($y^{⟨t⟩}$) for this time-step.

Figure 3: Basic RNN. The input sequence $x=(x^{⟨1⟩},x^{⟨2⟩},...,x^{⟨T_x⟩})$ is carried over $T_x$ time steps. The network outputs $y=(y^{⟨1⟩},y^{⟨2⟩},...,y^{⟨T_x⟩})$.

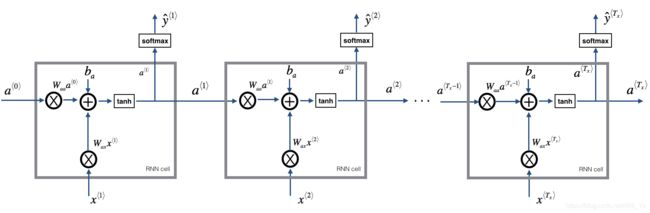
Exercise: Code the forward propagation of the RNN described in Figure (3).

Instructions:

1. Create a vector of zeros ($a$) that will store all the hidden states computed by the RNN.
2. Initialize the “next” hidden state as $a_0$ (initial hidden state).
3. Start looping over each time step, your incremental index is $t$ :
   • Update the “next” hidden state and the cache by running rnn_cell_forward
   • Store the “next” hidden state in $a$ ($t^{th}$ position)
   • Store the prediction in y
   • Add the cache to the list of caches
4. Return $a$, $y$ and caches

# GRADED FUNCTION: rnn_forward

def rnn_forward(x, a0, parameters):
    """
    Implement the forward propagation of the recurrent neural network described in Figure (3).

    Arguments:
    x -- Input data for every time-step, of shape (n_x, m, T_x).
    a0 -- Initial hidden state, of shape (n_a, m)
    parameters -- python dictionary containing:
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        ba --  Bias numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)

    Returns:
    a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
    y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
    caches -- tuple of values needed for the backward pass, contains (list of caches, x)
    """
    
    # Initialize "caches" which will contain the list of all caches
    caches = []
    
    # Retrieve dimensions from shapes of x and parameters["Wya"]
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wya"].shape
    
    ### START CODE HERE ###
    
    # initialize "a" and "y" with zeros (≈2 lines)
    a = np.zeros((n_a, m, T_x))
    y_pred = np.zeros((n_y, m, T_x))
    
    # Initialize a_next (≈1 line)
    a_next = a0
    
    # loop over all time-steps
    for t in range(T_x):
        # Update next hidden state, compute the prediction, get the cache (≈1 line)
        a_next, yt_pred, cache = rnn_cell_forward(x[:,:,t], a_next, parameters)
        # Save the value of the new "next" hidden state in a (≈1 line)
        a[:,:,t] = a_next
        # Save the value of the prediction in y (≈1 line)
        y_pred[:,:,t] = yt_pred
        # Append "cache" to "caches" (≈1 line)
        caches.append(cache)
        
    ### END CODE HERE ###
    
    # store values needed for backward propagation in cache
    caches = (caches, x)
    
    return a, y_pred, caches

np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}

a, y_pred, caches = rnn_forward(x, a0, parameters)
print("a[4][1] = ", a[4][1])
print("a.shape = ", a.shape)
print("y_pred[1][3] =", y_pred[1][3])
print("y_pred.shape = ", y_pred.shape)
print("caches[1][1][3] =", caches[1][1][3])
print("len(caches) = ", len(caches))

a[4][1] =  [-0.99999375  0.77911235 -0.99861469 -0.99833267]
a.shape =  (5, 10, 4)
y_pred[1][3] = [ 0.79560373  0.86224861  0.11118257  0.81515947]
y_pred.shape =  (2, 10, 4)
caches[1][1][3] = [-1.1425182  -0.34934272 -0.20889423  0.58662319]
len(caches) =  2

Expected Output:

a[4][1]:	[-0.99999375 0.77911235 -0.99861469 -0.99833267]
a.shape:	(5, 10, 4)
y[1][3]:	[ 0.79560373 0.86224861 0.11118257 0.81515947]
y.shape:	(2, 10, 4)
cache[1][1][3]:	[-1.1425182 -0.34934272 -0.20889423 0.58662319]
len(cache):	2

Congratulations! You’ve successfully built the forward propagation of a recurrent neural network from scratch. This will work well enough for some applications, but it suffers from vanishing gradient problems. So it works best when each output $y^{⟨t⟩}$ can be estimated using mainly “local” context (meaning information from inputs $x^{⟨t^{\prime }⟩}$ where $t^{\prime }$ is not too far from $t$).

In the next part, you will build a more complex LSTM model, which is better at addressing vanishing gradients. The LSTM will be better able to remember a piece of information and keep it saved for many timesteps.

2 - Long Short-Term Memory (LSTM) network

This following figure shows the operations of an LSTM-cell.

Figure 4: LSTM-cell. This tracks and updates a “cell state” or memory variable $c^{⟨t⟩}$ at every time-step, which can be different from $a^{⟨t⟩}$.

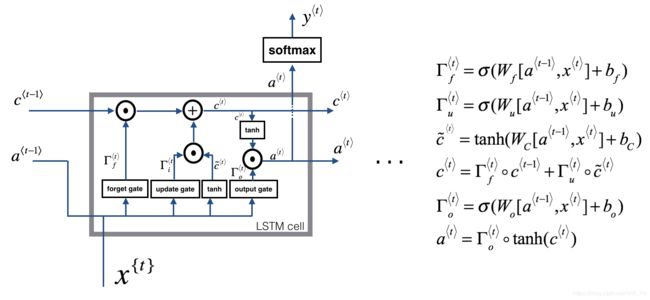
Similar to the RNN example above, you will start by implementing the LSTM cell for a single time-step. Then you can iteratively call it from inside a for-loop to have it process an input with $T_x$ time-steps.

About the gates

- Forget gate

For the sake of this illustration, lets assume we are reading words in a piece of text, and want use an LSTM to keep track of grammatical structures, such as whether the subject is singular or plural. If the subject changes from a singular word to a plural word, we need to find a way to get rid of our previously stored memory value of the singular/plural state. In an LSTM, the forget gate lets us do this:

$${\Gamma }_f^{⟨t⟩}=\sigma (W_f[a^{⟨t-1⟩},x^{⟨t⟩}]+b_f)\text{\hspace{1em}(1)}$$

Here, $W_f$ are weights that govern the forget gate’s behavior. We concatenate $[a^{⟨t-1⟩},x^{⟨t⟩}]$ and multiply by $W_f$. The equation above results in a vector ${\Gamma }_f^{⟨t⟩}$ with values between 0 and 1. This forget gate vector will be multiplied element-wise by the previous cell state $c^{⟨t-1⟩}$. So if one of the values of ${\Gamma }_f^{⟨t⟩}$ is 0 (or close to 0) then it means that the LSTM should remove that piece of information (e.g. the singular subject) in the corresponding component of $c^{⟨t-1⟩}$. If one of the values is 1, then it will keep the information.

- Update gate

Once we forget that the subject being discussed is singular, we need to find a way to update it to reflect that the new subject is now plural. Here is the formulat for the update gate:

$${\Gamma }_u^{⟨t⟩}=\sigma (W_u[a^{⟨t-1⟩},x^{\{t\}}]+b_u)\text{\hspace{1em}(2)}$$

Similar to the forget gate, here ${\Gamma }_u^{⟨t⟩}$ is again a vector of values between 0 and 1. This will be multiplied element-wise with ${\tilde{c}}^{⟨t⟩}$, in order to compute $c^{⟨t⟩}$.

- Updating the cell

To update the new subject we need to create a new vector of numbers that we can add to our previous cell state. The equation we use is:

$${\tilde{c}}^{⟨t⟩}=\tanh (W_c[a^{⟨t-1⟩},x^{⟨t⟩}]+b_c)\text{\hspace{1em}(3)}$$

Finally, the new cell state is:

$$c^{⟨t⟩}={\Gamma }_f^{⟨t⟩}\ast c^{⟨t-1⟩}+{\Gamma }_u^{⟨t⟩}\ast {\tilde{c}}^{⟨t⟩}\text{\hspace{1em}(4)}$$

- Output gate

To decide which outputs we will use, we will use the following two formulas:

$${\Gamma }_o^{⟨t⟩}=\sigma (W_o[a^{⟨t-1⟩},x^{⟨t⟩}]+b_o)\text{\hspace{1em}(5)}$$
$$a^{⟨t⟩}={\Gamma }_o^{⟨t⟩}\ast \tanh (c^{⟨t⟩})\text{\hspace{1em}(6)}$$

Where in equation 5 you decide what to output using a sigmoid function and in equation 6 you multiply that by the $\tanh$ of the previous state.

2.1 - LSTM cell

Exercise: Implement the LSTM cell described in the Figure (3).

Instructions:

1. Concatenate $a^{⟨t-1⟩}$ and $x^{⟨t⟩}$ in a single matrix: $concat=\left[\begin{array}{c}{a}^{⟨t-1⟩}\\ x^{⟨t⟩}\end{array}\right]$
2. Compute all the formulas 1-6. You can use sigmoid() (provided) and np.tanh().
3. Compute the prediction $y^{⟨t⟩}$. You can use softmax() (provided).

# GRADED FUNCTION: lstm_cell_forward

def lstm_cell_forward(xt, a_prev, c_prev, parameters):
    """
    Implement a single forward step of the LSTM-cell as described in Figure (4)

    Arguments:
    xt -- your input data at timestep "t", numpy array of shape (n_x, m).
    a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
    c_prev -- Memory state at timestep "t-1", numpy array of shape (n_a, m)
    parameters -- python dictionary containing:
                        Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
                        bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
                        Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
                        bi -- Bias of the update gate, numpy array of shape (n_a, 1)
                        Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
                        bc --  Bias of the first "tanh", numpy array of shape (n_a, 1)
                        Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
                        bo --  Bias of the output gate, numpy array of shape (n_a, 1)
                        Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
                        
    Returns:
    a_next -- next hidden state, of shape (n_a, m)
    c_next -- next memory state, of shape (n_a, m)
    yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
    cache -- tuple of values needed for the backward pass, contains (a_next, c_next, a_prev, c_prev, xt, parameters)
    
    Note: ft/it/ot stand for the forget/update/output gates, cct stands for the candidate value (c tilde),
          c stands for the memory value
    """

    # Retrieve parameters from "parameters"
    Wf = parameters["Wf"]
    bf = parameters["bf"]
    Wi = parameters["Wi"]
    bi = parameters["bi"]
    Wc = parameters["Wc"]
    bc = parameters["bc"]
    Wo = parameters["Wo"]
    bo = parameters["bo"]
    Wy = parameters["Wy"]
    by = parameters["by"]
    
    # Retrieve dimensions from shapes of xt and Wy
    n_x, m = xt.shape
    n_y, n_a = Wy.shape

    ### START CODE HERE ###
    # Concatenate a_prev and xt (≈3 lines)
    concat = np.zeros((n_a + n_x, m))
    concat[: n_a, :] = a_prev  #中括号里 “: n_a” 指的是从第一行到第n_a行，这里的“：”是从1开始数的，不是从0
    concat[n_a :, :] = xt

    # Compute values for ft, it, cct, c_next, ot, a_next using the formulas given figure (4) (≈6 lines)
    ft = sigmoid(np.dot(Wf,concat)+bf)
    it = sigmoid(np.dot(Wi,concat)+bi)
    cct = np.tanh(np.dot(Wc,concat)+bc)
    c_next = ft*c_prev+it*cct
    ot = sigmoid(np.dot(Wo,concat)+bo)
    a_next = ot*np.tanh(c_next)
    
    # Compute prediction of the LSTM cell (≈1 line)
    yt_pred = softmax(np.dot(Wy, a_next) + by)
    ### END CODE HERE ###

    # store values needed for backward propagation in cache
    cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)

    return a_next, c_next, yt_pred, cache

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)
print("cache[1][3] =", cache[1][3])
print("len(cache) = ", len(cache))

a_next[4] =  [-0.66408471  0.0036921   0.02088357  0.22834167 -0.85575339  0.00138482
  0.76566531  0.34631421 -0.00215674  0.43827275]
a_next.shape =  (5, 10)
c_next[2] =  [ 0.63267805  1.00570849  0.35504474  0.20690913 -1.64566718  0.11832942
  0.76449811 -0.0981561  -0.74348425 -0.26810932]
c_next.shape =  (5, 10)
yt[1] = [ 0.79913913  0.15986619  0.22412122  0.15606108  0.97057211  0.31146381
  0.00943007  0.12666353  0.39380172  0.07828381]
yt.shape =  (2, 10)
cache[1][3] = [-0.16263996  1.03729328  0.72938082 -0.54101719  0.02752074 -0.30821874
  0.07651101 -1.03752894  1.41219977 -0.37647422]
len(cache) =  10

Expected Output:

a_next[4]:	[-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482 0.76566531 0.34631421 -0.00215674 0.43827275]
a_next.shape:	(5, 10)
c_next[2]:	[ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942 0.76449811 -0.0981561 -0.74348425 -0.26810932]
c_next.shape:	(5, 10)
yt[1]:	[ 0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381 0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape:	(2, 10)
cache[1][3]:	[-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874 0.07651101 -1.03752894 1.41219977 -0.37647422]
len(cache):	10

2.2 - Forward pass for LSTM

Now that you have implemented one step of an LSTM, you can now iterate this over this using a for-loop to process a sequence of $T_x$ inputs.

Figure 4: LSTM over multiple time-steps.

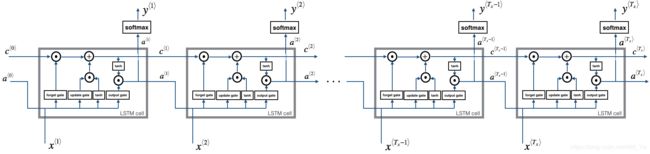
Exercise: Implement lstm_forward() to run an LSTM over $T_x$ time-steps.

Note: $c^{⟨0⟩}$ is initialized with zeros.

# GRADED FUNCTION: lstm_forward

def lstm_forward(x, a0, parameters):
    """
    Implement the forward propagation of the recurrent neural network using an LSTM-cell described in Figure (3).

    Arguments:
    x -- Input data for every time-step, of shape (n_x, m, T_x).
    a0 -- Initial hidden state, of shape (n_a, m)
    parameters -- python dictionary containing:
                        Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
                        bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
                        Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
                        bi -- Bias of the update gate, numpy array of shape (n_a, 1)
                        Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
                        bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
                        Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
                        bo -- Bias of the output gate, numpy array of shape (n_a, 1)
                        Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
                        
    Returns:
    a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
    y -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
    caches -- tuple of values needed for the backward pass, contains (list of all the caches, x)
    """

    # Initialize "caches", which will track the list of all the caches
    caches = []
    
    ### START CODE HERE ###
    # Retrieve dimensions from shapes of x and parameters['Wy'] (≈2 lines)
    n_x, m, T_x = x.shape
    n_y, n_a = parameters['Wy'].shape
    
    # initialize "a", "c" and "y" with zeros (≈3 lines)
    a = np.zeros((n_a,m,T_x))
    c = np.zeros((n_a,m,T_x))
    y = np.zeros((n_y,m,T_x))
    
    # Initialize a_next and c_next (≈2 lines)
    a_next = a0
    c_next = np.zeros((n_a,m))
    
    # loop over all time-steps
    for t in range(T_x):
        # Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
        a_next, c_next, yt, cache = lstm_cell_forward(x[:,:,t], a_next, c_next, parameters)
        # Save the value of the new "next" hidden state in a (≈1 line)
        a[:,:,t] = a_next
        # Save the value of the prediction in y (≈1 line)
        y[:,:,t] = yt
        # Save the value of the next cell state (≈1 line)
        c[:,:,t]  = c_next
        # Append the cache into caches (≈1 line)
        caches.append(cache)
        
    ### END CODE HERE ###
    
    # store values needed for backward propagation in cache
    caches = (caches, x)

    return a, y, c, caches

np.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a, y, c, caches = lstm_forward(x, a0, parameters)
print("a[4][3][6] = ", a[4][3][6])
print("a.shape = ", a.shape)
print("y[1][4][3] =", y[1][4][3])
print("y.shape = ", y.shape)
print("caches[1][1[1]] =", caches[1][1][1])
print("c[1][2][1]", c[1][2][1])
print("len(caches) = ", len(caches))

a[4][3][6] =  0.172117767533
a.shape =  (5, 10, 7)
y[1][4][3] = 0.95087346185
y.shape =  (2, 10, 7)
caches[1][1[1]] = [ 0.82797464  0.23009474  0.76201118 -0.22232814 -0.20075807  0.18656139
  0.41005165]
c[1][2][1] -0.855544916718
len(caches) =  2

Expected Output:

a[4][3][6] =	0.172117767533
a.shape =	(5, 10, 7)
y[1][4][3] =	0.95087346185
y.shape =	(2, 10, 7)
caches[1][1][1] =	[ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139 0.41005165]
c[1][2][1] =	-0.855544916718
len(caches) =	2

Congratulations! You have now implemented the forward passes for the basic RNN and the LSTM. When using a deep learning framework, implementing the forward pass is sufficient to build systems that achieve great performance.

The rest of this notebook is optional, and will not be graded.

3 - Backpropagation in recurrent neural networks (OPTIONAL / UNGRADED)

In modern deep learning frameworks, you only have to implement the forward pass, and the framework takes care of the backward pass, so most deep learning engineers do not need to bother with the details of the backward pass. If however you are an expert in calculus and want to see the details of backprop in RNNs, you can work through this optional portion of the notebook.

When in an earlier course you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in recurrent neural networks you can to calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are quite complicated and we did not derive them in lecture. However, we will briefly present them below.

3.1 - Basic RNN backward pass

We will start by computing the backward pass for the basic RNN-cell.

Figure 5: RNN-cell’s backward pass. Just like in a fully-connected neural network, the derivative of the cost function $J$ backpropagates through the RNN by following the chain-rule from calculas. The chain-rule is also used to calculate $(\frac{\partial J}{\partial W_{ax}},\frac{\partial J}{\partial W_{aa}},\frac{\partial J}{\partial b})$ to update the parameters $(W_{ax},W_{aa},b_a)$.

Deriving the one step backward functions:

To compute the rnn_cell_backward you need to compute the following equations. It is a good exercise to derive them by hand.

The derivative of $\tanh$ is $1-\tanh (x{)}^2$. You can find the complete proof here. Note that: $\text{sech}(x{)}^2=1-\tanh (x{)}^2$

Similarly for $\frac{\partial a^{⟨t⟩}}{\partial W_{ax}},\frac{\partial a^{⟨t⟩}}{\partial W_{aa}},\frac{\partial a^{⟨t⟩}}{\partial b}$, the derivative of $\tanh (u)$ is $(1-\tanh (u{)}^2)du$.

The final two equations also follow same rule and are derived using the $\tanh$ derivative. Note that the arrangement is done in a way to get the same dimensions to match.

def rnn_cell_backward(da_next, cache):
    """
    Implements the backward pass for the RNN-cell (single time-step).

    Arguments:
    da_next -- Gradient of loss with respect to next hidden state
    cache -- python dictionary containing useful values (output of rnn_cell_forward())

    Returns:
    gradients -- python dictionary containing:
                        dx -- Gradients of input data, of shape (n_x, m)
                        da_prev -- Gradients of previous hidden state, of shape (n_a, m)
                        dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
                        dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
                        dba -- Gradients of bias vector, of shape (n_a, 1)
    """
    
    # Retrieve values from cache
    (a_next, a_prev, xt, parameters) = cache
    
    # Retrieve values from parameters
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]

    ### START CODE HERE ###
    # compute the gradient of tanh with respect to a_next (≈1 line)
    dtanh = (1-a_next**2)*da_next #图5中公式2

    # compute the gradient of the loss with respect to Wax (≈2 lines)
    dxt = np.dot(np.transpose(Wax), dtanh)
    dWax = np.dot(dtanh, np.transpose(xt))

    # compute the gradient with respect to Waa (≈2 lines)
    da_prev = np.dot(np.transpose(Waa), dtanh) 
    dWaa = np.dot(dtanh, np.transpose(a_prev))

    # compute the gradient with respect to b (≈1 line)
    dba = np.sum(dtanh, keepdims=True, axis=1)

    ### END CODE HERE ###
    
    # Store the gradients in a python dictionary
    gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
    
    return gradients

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
b = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}

a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)

da_next = np.random.randn(5,10)
gradients = rnn_cell_backward(da_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)

np.random.seed(1)

xt = np.random.randn(3,10)

a_prev = np.random.randn(5,10)

Wax = np.random.randn(5,3)

Waa = np.random.randn(5,5)

Wya = np.random.randn(2,5)

b = np.random.randn(5,1)

by = np.random.randn(2,1)

parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}

​

a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)

​

da_next = np.random.randn(5,10)

gradients = rnn_cell_backward(da_next, cache)

print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])

print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)

print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])

print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)

print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])

print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)

print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])

print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)

print("gradients[\"dba\"][4] =", gradients["dba"][4])

print("gradients[\"dba\"].shape =", gradients["dba"].shape)

gradients["dxt"][1][2] = -0.460564103059
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = 0.0842968653807
gradients["da_prev"].shape = (5, 10)
gradients["dWax"][3][1] = 0.393081873922
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = -0.28483955787
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [ 0.80517166]
gradients["dba"].shape = (5, 1)

Expected Output:

**gradients["dxt"][1][2]** =	-0.460564103059
**gradients["dxt"].shape** =	(3, 10)
**gradients["da_prev"][2][3]** =	0.0842968653807
**gradients["da_prev"].shape** =	(5, 10)
**gradients["dWax"][3][1]** =	0.393081873922
**gradients["dWax"].shape** =	(5, 3)
**gradients["dWaa"][1][2]** =	-0.28483955787
**gradients["dWaa"].shape** =	(5, 5)
**gradients["dba"][4]** =	[ 0.80517166]
**gradients["dba"].shape** =	(5, 1)

Backward pass through the RNN

Computing the gradients of the cost with respect to $a^{⟨t⟩}$ at every time-step $t$ is useful because it is what helps the gradient backpropagate to the previous RNN-cell. To do so, you need to iterate through all the time steps starting at the end, and at each step, you increment the overall $d{b}_a$, $d{W}_{aa}$, $d{W}_{ax}$ and you store $dx$.

Instructions:

Implement the rnn_backward function. Initialize the return variables with zeros first and then loop through all the time steps while calling the rnn_cell_backward at each time timestep, update the other variables accordingly.

def rnn_backward(da, caches):
    """
    Implement the backward pass for a RNN over an entire sequence of input data.

    Arguments:
    da -- Upstream gradients of all hidden states, of shape (n_a, m, T_x)
    caches -- tuple containing information from the forward pass (rnn_forward)
    
    Returns:
    gradients -- python dictionary containing:
                        dx -- Gradient w.r.t. the input data, numpy-array of shape (n_x, m, T_x)
                        da0 -- Gradient w.r.t the initial hidden state, numpy-array of shape (n_a, m)
                        dWax -- Gradient w.r.t the input's weight matrix, numpy-array of shape (n_a, n_x)
                        dWaa -- Gradient w.r.t the hidden state's weight matrix, numpy-arrayof shape (n_a, n_a)
                        dba -- Gradient w.r.t the bias, of shape (n_a, 1)
    """
        
    ### START CODE HERE ###
    
    # Retrieve values from the first cache (t=1) of caches (≈2 lines)
    (caches, x) = caches
    (a1, a0, x1, parameters) = caches[0]
    
    # Retrieve dimensions from da's and x1's shapes (≈2 lines)
    n_a, m, T_x = da.shape
    n_x, m = x1.shape
    
    # initialize the gradients with the right sizes (≈6 lines)
    dx = np.zeros((n_x, m, T_x))
    dWax = np.zeros((n_a,n_x))
    dWaa = np.zeros((n_a, n_a))
    dba = np.zeros((n_a, 1))
    da0 = np.zeros((n_a, m))
    da_prevt = np.zeros((n_a,m))
    
    # Loop through all the time steps
    for t in reversed(range(T_x)):
        # Compute gradients at time step t. Choose wisely the "da_next" and the "cache" to use in the backward propagation step. (≈1 line)
        gradients = rnn_cell_backward(da[:,:,t]+da_prevt, caches[t])
        # Retrieve derivatives from gradients (≈ 1 line)
        dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
        # Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)
        dx[:, :, t] = dxt
        dWax += dWaxt
        dWaa += dWaat
        dba += dbat
        
    # Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line) 
    da0 = da_prevt
    ### END CODE HERE ###

    # Store the gradients in a python dictionary
    gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
    
    return gradients

np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)

print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)

gradients["dx"][1][2] = [-2.07101689 -0.59255627  0.02466855  0.01483317]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.314942375127
gradients["da0"].shape = (5, 10)
gradients["dWax"][3][1] = 11.2641044965
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = 2.30333312658
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [-0.74747722]
gradients["dba"].shape = (5, 1)

Expected Output:

**gradients["dx"][1][2]** =	[-2.07101689 -0.59255627 0.02466855 0.01483317]
**gradients["dx"].shape** =	(3, 10, 4)
**gradients["da0"][2][3]** =	-0.314942375127
**gradients["da0"].shape** =	(5, 10)
**gradients["dWax"][3][1]** =	11.2641044965
**gradients["dWax"].shape** =	(5, 3)
**gradients["dWaa"][1][2]** =	2.30333312658
**gradients["dWaa"].shape** =	(5, 5)
**gradients["dba"][4]** =	[-0.74747722]
**gradients["dba"].shape** =	(5, 1)

3.2 - LSTM backward pass

3.2.1 One Step backward

The LSTM backward pass is slighltly more complicated than the forward one. We have provided you with all the equations for the LSTM backward pass below. (If you enjoy calculus exercises feel free to try deriving these from scratch yourself.)

3.2.2 gate derivatives

$$d{\Gamma }_o^{⟨t⟩}=d{a}_{next}\ast \tanh (c_{next})\ast {\Gamma }_o^{⟨t⟩}\ast (1-{\Gamma }_o^{⟨t⟩})\text{\hspace{1em}(7)}$$

$$d{\tilde{c}}^{⟨t⟩}=d{c}_{next}\ast {\Gamma }_u^{⟨t⟩}+{\Gamma }_o^{⟨t⟩}(1-\tanh (c_{next}{)}^2)\ast i_t\ast d{a}_{next}\ast {\tilde{c}}^{⟨t⟩}\ast (1-\tanh (\tilde{c}{)}^2)\text{\hspace{1em}(8)}$$

$$d{\Gamma }_u^{⟨t⟩}=d{c}_{next}\ast {\tilde{c}}^{⟨t⟩}+{\Gamma }_o^{⟨t⟩}(1-\tanh (c_{next}{)}^2)\ast {\tilde{c}}^{⟨t⟩}\ast d{a}_{next}\ast {\Gamma }_u^{⟨t⟩}\ast (1-{\Gamma }_u^{⟨t⟩})\text{\hspace{1em}(9)}$$

$$d{\Gamma }_f^{⟨t⟩}=d{c}_{next}\ast {\tilde{c}}_{prev}+{\Gamma }_o^{⟨t⟩}(1-\tanh (c_{next}{)}^2)\ast c_{prev}\ast d{a}_{next}\ast {\Gamma }_f^{⟨t⟩}\ast (1-{\Gamma }_f^{⟨t⟩})\text{\hspace{1em}(10)}$$

3.2.3 parameter derivatives

$$d{W}_f=d{\Gamma }_f^{⟨t⟩}\ast {\left(\begin{array}{c}{a}_{prev}\\ x_t\end{array}\right)}^T\text{\hspace{1em}(11)}$$
$$d{W}_u=d{\Gamma }_u^{⟨t⟩}\ast {\left(\begin{array}{c}{a}_{prev}\\ x_t\end{array}\right)}^T\text{\hspace{1em}(12)}$$
$$d{W}_c=d{\tilde{c}}^{⟨t⟩}\ast {\left(\begin{array}{c}{a}_{prev}\\ x_t\end{array}\right)}^T\text{\hspace{1em}(13)}$$
$$d{W}_o=d{\Gamma }_o^{⟨t⟩}\ast {\left(\begin{array}{c}{a}_{prev}\\ x_t\end{array}\right)}^T\text{\hspace{1em}(14)}$$

To calculate $d{b}_f,d{b}_u,d{b}_c,d{b}_o$ you just need to sum across the horizontal (axis= 1) axis on $d{\Gamma }_f^{⟨t⟩},d{\Gamma }_u^{⟨t⟩},d{\tilde{c}}^{⟨t⟩},d{\Gamma }_o^{⟨t⟩}$ respectively. Note that you should have the keep_dims = True option.

Finally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.

$$d{a}_{prev}=W_f^T\ast d{\Gamma }_f^{⟨t⟩}+W_u^T\ast d{\Gamma }_u^{⟨t⟩}+W_c^T\ast d{\tilde{c}}^{⟨t⟩}+W_o^T\ast d{\Gamma }_o^{⟨t⟩}\text{\hspace{1em}(15)}$$
Here, the weights for equations 13 are the first n_a, (i.e. $W_f=W_f[:n_a,:]$ etc…)

$$d{c}_{prev}=d{c}_{next}{\Gamma }_f^{⟨t⟩}+{\Gamma }_o^{⟨t⟩}\ast (1-\tanh (c_{next}{)}^2)\ast {\Gamma }_f^{⟨t⟩}\ast d{a}_{next}\text{\hspace{1em}(16)}$$
$$d{x}^{⟨t⟩}=W_f^T\ast d{\Gamma }_f^{⟨t⟩}+W_u^T\ast d{\Gamma }_u^{⟨t⟩}+W_c^T\ast d{\tilde{c}}_t+W_o^T\ast d{\Gamma }_o^{⟨t⟩}\text{\hspace{1em}(17)}$$
where the weights for equation 15 are from n_a to the end, (i.e. $W_f=W_f[n_a:,:]$ etc…)

Exercise: Implement lstm_cell_backward by implementing equations $7-17$ below. Good luck! ?

def lstm_cell_backward(da_next, dc_next, cache):
    """
    Implement the backward pass for the LSTM-cell (single time-step).

    Arguments:
    da_next -- Gradients of next hidden state, of shape (n_a, m)
    dc_next -- Gradients of next cell state, of shape (n_a, m)
    cache -- cache storing information from the forward pass

    Returns:
    gradients -- python dictionary containing:
                        dxt -- Gradient of input data at time-step t, of shape (n_x, m)
                        da_prev -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
                        dc_prev -- Gradient w.r.t. the previous memory state, of shape (n_a, m, T_x)
                        dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
                        dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
                        dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
                        dWo -- Gradient w.r.t. the weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
                        dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
                        dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
                        dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
                        dbo -- Gradient w.r.t. biases of the output gate, of shape (n_a, 1)
    """

    # Retrieve information from "cache"
    (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
    
    ### START CODE HERE ###
    # Retrieve dimensions from xt's and a_next's shape (≈2 lines)
    n_x, m = xt.shape
    n_a, m = a_next.shape
    
    # Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
    dot = da_next*np.tanh(c_next)*ot*(1-ot)
    dcct = (dc_next*it+ot*(1-np.square(np.tanh(c_next)))*it*da_next)*(1-np.square(cct))
    dit = (dc_next*cct+ot*(1-np.square(np.tanh(c_next)))*cct*da_next)*it*(1-it)
    dft = (dc_next*c_prev+ot*(1-np.square(np.tanh(c_next)))*c_prev*da_next)*ft*(1-ft) 

    # Code equations (7) to (10) (≈4 lines)
    #dit = None  #出问题了？？？
    #dft = None
    #dot = None
    #dcct = None

    # Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
    dWf = np.dot(dft,np.concatenate((a_prev, xt), axis=0).T)
    dWi = np.dot(dit,np.concatenate((a_prev, xt), axis=0).T)
    dWc = np.dot(dcct,np.concatenate((a_prev, xt), axis=0).T)
    dWo = np.dot(dot,np.concatenate((a_prev, xt), axis=0).T) 
    dbf = np.sum(dft,axis=1,keepdims=True)
    dbi = np.sum(dit,axis=1,keepdims=True)
    dbc = np.sum(dcct,axis=1,keepdims=True)
    dbo = np.sum(dot,axis=1,keepdims=True)

    # Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
    da_prev = np.dot(parameters['Wf'][:,:n_a].T, dft) + np.dot(parameters['Wi'][:,:n_a].T, dit) + np.dot(parameters['Wc'][:,:n_a].T, dcct) + np.dot(parameters['Wo'][:,:n_a].T, dot)
    dc_prev = dc_next*ft+ot*(1-np.square(np.tanh(c_next)))*ft*da_next
    dxt = np.dot(parameters['Wf'][:,n_a:].T,dft)+np.dot(parameters['Wi'][:,n_a:].T,dit)+np.dot(parameters['Wc'][:,n_a:].T,dcct)+np.dot(parameters['Wo'][:,n_a:].T,dot)
    ### END CODE HERE ###
    
    # Save gradients in dictionary
    gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
                "dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}

    return gradients

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)

da_next = np.random.randn(5,10)
dc_next = np.random.randn(5,10)
gradients = lstm_cell_backward(da_next, dc_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)

gradients["dxt"][1][2] = 3.23055911511
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = -0.0639621419711
gradients["da_prev"].shape = (5, 10)
gradients["dc_prev"][2][3] = 0.797522038797
gradients["dc_prev"].shape = (5, 10)
gradients["dWf"][3][1] = -0.147954838164
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 1.05749805523
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = 2.30456216369
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.331311595289
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [ 0.18864637]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.40142491]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [ 0.25587763]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [ 0.13893342]
gradients["dbo"].shape = (5, 1)

Expected Output:

**gradients["dxt"][1][2]** =	3.23055911511
**gradients["dxt"].shape** =	(3, 10)
**gradients["da_prev"][2][3]** =	-0.0639621419711
**gradients["da_prev"].shape** =	(5, 10)
**gradients["dc_prev"][2][3]** =	0.797522038797
**gradients["dc_prev"].shape** =	(5, 10)
**gradients["dWf"][3][1]** =	-0.147954838164
**gradients["dWf"].shape** =	(5, 8)
**gradients["dWi"][1][2]** =	1.05749805523
**gradients["dWi"].shape** =	(5, 8)
**gradients["dWc"][3][1]** =	2.30456216369
**gradients["dWc"].shape** =	(5, 8)
**gradients["dWo"][1][2]** =	0.331311595289
**gradients["dWo"].shape** =	(5, 8)
**gradients["dbf"][4]** =	[ 0.18864637]
**gradients["dbf"].shape** =	(5, 1)
**gradients["dbi"][4]** =	[-0.40142491]
**gradients["dbi"].shape** =	(5, 1)
**gradients["dbc"][4]** =	[ 0.25587763]
**gradients["dbc"].shape** =	(5, 1)
**gradients["dbo"][4]** =	[ 0.13893342]
**gradients["dbo"].shape** =	(5, 1)

3.3 Backward pass through the LSTM RNN

This part is very similar to the rnn_backward function you implemented above. You will first create variables of the same dimension as your return variables. You will then iterate over all the time steps starting from the end and call the one step function you implemented for LSTM at each iteration. You will then update the parameters by summing them individually. Finally return a dictionary with the new gradients.

Instructions: Implement the lstm_backward function. Create a for loop starting from $T_x$ and going backward. For each step call lstm_cell_backward and update the your old gradients by adding the new gradients to them. Note that dxt is not updated but is stored.

def lstm_backward(da, caches):
    
    """
    Implement the backward pass for the RNN with LSTM-cell (over a whole sequence).

    Arguments:
    da -- Gradients w.r.t the hidden states, numpy-array of shape (n_a, m, T_x)
    dc -- Gradients w.r.t the memory states, numpy-array of shape (n_a, m, T_x)
    caches -- cache storing information from the forward pass (lstm_forward)

    Returns:
    gradients -- python dictionary containing:
                        dx -- Gradient of inputs, of shape (n_x, m, T_x)
                        da0 -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
                        dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
                        dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
                        dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
                        dWo -- Gradient w.r.t. the weight matrix of the save gate, numpy array of shape (n_a, n_a + n_x)
                        dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
                        dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
                        dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
                        dbo -- Gradient w.r.t. biases of the save gate, of shape (n_a, 1)
    """

    # Retrieve values from the first cache (t=1) of caches.
    (caches, x) = caches
    (a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
    
    ### START CODE HERE ###
    # Retrieve dimensions from da's and x1's shapes (≈2 lines)
    n_a, m, T_x = da.shape
    n_x, m = x1.shape
    
    # initialize the gradients with the right sizes (≈12 lines)
    dx = np.zeros((n_x,m,T_x))
    da0 = np.zeros((n_a,m))
    da_prevt = np.zeros((n_a,m))
    dc_prevt = np.zeros((n_a,m))
    dWf = np.zeros((n_a,n_a+n_x))
    dWi = np.zeros((n_a,n_a+n_x))
    dWc = np.zeros((n_a,n_a+n_x))
    dWo = np.zeros((n_a,n_a+n_x))
    dbf = np.zeros((n_a,1))
    dbi = np.zeros((n_a,1))
    dbc = np.zeros((n_a,1))
    dbo = np.zeros((n_a,1))
    
    # loop back over the whole sequence
    for t in reversed(range(T_x)):
        # Compute all gradients using lstm_cell_backward
        gradients = lstm_cell_backward(da[:,:,t]+da_prevt,dc_prevt,caches[t]) 
        # Store or add the gradient to the parameters' previous step's gradient
        dx[:,:,t] = gradients['dxt']
        dWf = dWf+gradients['dWf']
        dWi = dWi+gradients['dWi']
        dWc = dWc+gradients['dWc']
        dWo = dWo+gradients['dWo']
        dbf = dbf+gradients['dbf']
        dbi = dbi+gradients['dbi']
        dbc = dbc+gradients['dbc']
        dbo = dbo+gradients['dbo']
    # Set the first activation's gradient to the backpropagated gradient da_prev.
    da0 = gradients['da_prev']
    
    ### END CODE HERE ###

    # Store the gradients in a python dictionary
    gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
                "dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
    
    return gradients

np.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a, y, c, caches = lstm_forward(x, a0, parameters)

da = np.random.randn(5, 10, 4)
gradients = lstm_backward(da, caches)

print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)

gradients["dx"][1][2] = [-0.00173313  0.08287442 -0.30545663 -0.43281115]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.095911501954
gradients["da0"].shape = (5, 10)
gradients["dWf"][3][1] = -0.0698198561274
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 0.102371820249
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = -0.0624983794927
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.0484389131444
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [-0.0565788]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.15399065]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [-0.29691142]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [-0.29798344]
gradients["dbo"].shape = (5, 1)

Expected Output:

**gradients["dx"][1][2]** =	[-0.00173313 0.08287442 -0.30545663 -0.43281115]
**gradients["dx"].shape** =	(3, 10, 4)
**gradients["da0"][2][3]** =	-0.095911501954
**gradients["da0"].shape** =	(5, 10)
**gradients["dWf"][3][1]** =	-0.0698198561274
**gradients["dWf"].shape** =	(5, 8)
**gradients["dWi"][1][2]** =	0.102371820249
**gradients["dWi"].shape** =	(5, 8)
**gradients["dWc"][3][1]** =	-0.0624983794927
**gradients["dWc"].shape** =	(5, 8)
**gradients["dWo"][1][2]** =	0.0484389131444
**gradients["dWo"].shape** =	(5, 8)
**gradients["dbf"][4]** =	[-0.0565788]
**gradients["dbf"].shape** =	(5, 1)
**gradients["dbi"][4]** =	[-0.06997391]
**gradients["dbi"].shape** =	(5, 1)
**gradients["dbc"][4]** =	[-0.27441821]
**gradients["dbc"].shape** =	(5, 1)
**gradients["dbo"][4]** =	[ 0.16532821]
**gradients["dbo"].shape** =	(5, 1)

Congratulations !

Congratulations on completing this assignment. You now understand how recurrent neural networks work!

Lets go on to the next exercise, where you’ll use an RNN to build a character-level language model.

---

Part 2

Character level language model - Dinosaurus land

Welcome to Dinosaurus Island! 65 million years ago, dinosaurs existed, and in this assignment they are back. You are in charge of a special task. Leading biology researchers are creating new breeds of dinosaurs and bringing them to life on earth, and your job is to give names to these dinosaurs. If a dinosaur does not like its name, it might go beserk, so choose wisely!
Luckily you have learned some deep learning and you will use it to save the day. Your assistant has collected a list of all the dinosaur names they could find, and compiled them into this dataset. (Feel free to take a look by clicking the previous link.) To create new dinosaur names, you will build a character level language model to generate new names. Your algorithm will learn the different name patterns, and randomly generate new names. Hopefully this algorithm will keep you and your team safe from the dinosaurs’ wrath!

By completing this assignment you will learn:

• How to store text data for processing using an RNN
• How to synthesize data, by sampling predictions at each time step and passing it to the next RNN-cell unit
• How to build a character-level text generation recurrent neural network
• Why clipping the gradients is important

We will begin by loading in some functions that we have provided for you in rnn_utils. Specifically, you have access to functions such as rnn_forward and rnn_backward which are equivalent to those you’ve implemented in the previous assignment.

import numpy as np
from utils import *
import random

1 - Problem Statement

1.1 - Dataset and Preprocessing

Run the following cell to read the dataset of dinosaur names, create a list of unique characters (such as a-z), and compute the dataset and vocabulary size.

data = open('dinos.txt', 'r').read()
data= data.lower()
chars = list(set(data))
data_size, vocab_size = len(data), len(chars)
print('There are %d total characters and %d unique characters in your data.' % (data_size, vocab_size))

There are 19909 total characters and 27 unique characters in your data.

The characters are a-z (26 characters) plus the “\n” (or newline character), which in this assignment plays a role similar to the (or “End of sentence”) token we had discussed in lecture, only here it indicates the end of the dinosaur name rather than the end of a sentence. In the cell below, we create a python dictionary (i.e., a hash table) to map each character to an index from 0-26. We also create a second python dictionary that maps each index back to the corresponding character character. This will help you figure out what index corresponds to what character in the probability distribution output of the softmax layer. Below, char_to_ix and ix_to_char are the python dictionaries.

char_to_ix = { ch:i for i,ch in enumerate(sorted(chars)) }
ix_to_char = { i:ch for i,ch in enumerate(sorted(chars)) }
print(ix_to_char)

{0: '\n', 1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z'}

1.2 - Overview of the model

Your model will have the following structure:

• Initialize parameters
• Run the optimization loop
  • Forward propagation to compute the loss function
  • Backward propagation to compute the gradients with respect to the loss function
  • Clip the gradients to avoid exploding gradients
  • Using the gradients, update your parameter with the gradient descent update rule.
• Return the learned parameters

Figure 1: Recurrent Neural Network, similar to what you had built in the previous notebook “Building a RNN - Step by Step”.

At each time-step, the RNN tries to predict what is the next character given the previous characters. The dataset $X=(x^{⟨1⟩},x^{⟨2⟩},...,x^{⟨T_x⟩})$ is a list of characters in the training set, while $Y=(y^{⟨1⟩},y^{⟨2⟩},...,y^{⟨T_x⟩})$ is such that at every time-step $t$, we have $y^{⟨t⟩}=x^{⟨t+1⟩}$.

2 - Building blocks of the model

In this part, you will build two important blocks of the overall model:

• Gradient clipping: to avoid exploding gradients
• Sampling: a technique used to generate characters

You will then apply these two functions to build the model.

2.1 - Clipping the gradients in the optimization loop

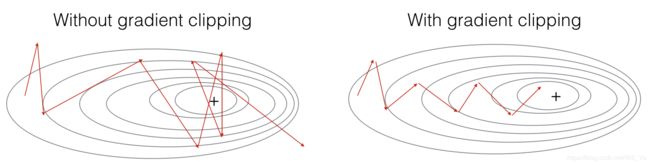
In this section you will implement the clip function that you will call inside of your optimization loop. Recall that your overall loop structure usually consists of a forward pass, a cost computation, a backward pass, and a parameter update. Before updating the parameters, you will perform gradient clipping when needed to make sure that your gradients are not “exploding,” meaning taking on overly large values.

In the exercise below, you will implement a function clip that takes in a dictionary of gradients and returns a clipped version of gradients if needed. There are different ways to clip gradients; we will use a simple element-wise clipping procedure, in which every element of the gradient vector is clipped to lie between some range [-N, N]. More generally, you will provide a maxValue (say 10). In this example, if any component of the gradient vector is greater than 10, it would be set to 10; and if any component of the gradient vector is less than -10, it would be set to -10. If it is between -10 and 10, it is left alone.

**Figure 2**: Visualization of gradient descent with and without gradient clipping, in a case where the network is running into slight "exploding gradient" problems.

Exercise: Implement the function below to return the clipped gradients of your dictionary gradients. Your function takes in a maximum threshold and returns the clipped versions of your gradients. You can check out this hint for examples of how to clip in numpy. You will need to use the argument out = ....

### GRADED FUNCTION: clip

def clip(gradients, maxValue):
    '''
    Clips the gradients' values between minimum and maximum.
    
    Arguments:
    gradients -- a dictionary containing the gradients "dWaa", "dWax", "dWya", "db", "dby"
    maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue
    
    Returns: 
    gradients -- a dictionary with the clipped gradients.
    '''
    
    dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients['dby']
   
    ### START CODE HERE ###
    # clip to mitigate exploding gradients, loop over [dWax, dWaa, dWya, db, dby]. (≈2 lines)
    for gradient in [dWax, dWaa, dWya, db, dby]:
        np.clip(gradient,-maxValue,maxValue,out=gradient)
    ### END CODE HERE ###
    
    gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}
    
    return gradients

np.random.seed(3)
dWax = np.random.randn(5,3)*10
dWaa = np.random.randn(5,5)*10
dWya = np.random.randn(2,5)*10
db = np.random.randn(5,1)*10
dby = np.random.randn(2,1)*10
gradients = {"dWax": dWax, "dWaa": dWaa, "dWya": dWya, "db": db, "dby": dby}
gradients = clip(gradients, 10)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])

gradients["dWaa"][1][2] = 10.0
gradients["dWax"][3][1] = -10.0
gradients["dWya"][1][2] = 0.29713815361
gradients["db"][4] = [ 10.]
gradients["dby"][1] = [ 8.45833407]

** Expected output:**

**gradients["dWaa"][1][2] **	10.0
**gradients["dWax"][3][1]**	-10.0
**gradients["dWya"][1][2]**	0.29713815361
**gradients["db"][4]**	[ 10.]
**gradients["dby"][1]**	[ 8.45833407]

2.2 - Sampling

Now assume that your model is trained. You would like to generate new text (characters). The process of generation is explained in the picture below:

Figure 3: In this picture, we assume the model is already trained. We pass in $x^{⟨1⟩}=0$ at the first time step, and have the network then sample one character at a time.

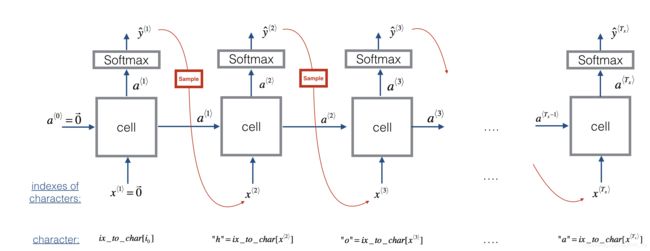
Exercise: Implement the sample function below to sample characters. You need to carry out 4 steps:

• Step 1: Pass the network the first “dummy” input $x^{⟨1⟩}=0$ (the vector of zeros). This is the default input before we’ve generated any characters. We also set $a^{⟨0⟩}=0$

• Step 2: Run one step of forward propagation to get $a^{⟨1⟩}$ and ${\hat{y}}^{⟨1⟩}$. Here are the equations:

$$a^{⟨t+1⟩}=\tanh (W_{ax}{x}^{⟨t⟩}+W_{aa}{a}^{⟨t⟩}+b)\text{\hspace{1em}(1)}$$

$$z^{⟨t+1⟩}=W_{ya}{a}^{⟨t+1⟩}+b_y\text{\hspace{1em}(2)}$$

$${\hat{y}}^{⟨t+1⟩}=softmax(z^{⟨t+1⟩})\text{\hspace{1em}(3)}$$

Note that ${\hat{y}}^{⟨t+1⟩}$ is a (softmax) probability vector (its entries are between 0 and 1 and sum to 1). ${\hat{y}}_i^{⟨t+1⟩}$ represents the probability that the character indexed by “i” is the next character. We have provided a softmax() function that you can use.

• Step 3: Carry out sampling: Pick the next character’s index according to the probability distribution specified by ${\hat{y}}^{⟨t+1⟩}$. This means that if ${\hat{y}}_i^{⟨t+1⟩}=0.16$, you will pick the index “i” with 16% probability. To implement it, you can use np.random.choice.

Here is an example of how to use np.random.choice():

np.random.seed(0)
p = np.array([0.1, 0.0, 0.7, 0.2])
index = np.random.choice([0, 1, 2, 3], p = p.ravel())

This means that you will pick the index according to the distribution:
$P(index=0)=0.1,P(index=1)=0.0,P(index=2)=0.7,P(index=3)=0.2$.

• Step 4: The last step to implement in sample() is to overwrite the variable x, which currently stores $x^{⟨t⟩}$, with the value of $x^{⟨t+1⟩}$. You will represent $x^{⟨t+1⟩}$ by creating a one-hot vector corresponding to the character you’ve chosen as your prediction. You will then forward propagate $x^{⟨t+1⟩}$ in Step 1 and keep repeating the process until you get a “\n” character, indicating you’ve reached the end of the dinosaur name.

# GRADED FUNCTION: sample

def sample(parameters, char_to_ix, seed):
    """
    Sample a sequence of characters according to a sequence of probability distributions output of the RNN

    Arguments:
    parameters -- python dictionary containing the parameters Waa, Wax, Wya, by, and b. 
    char_to_ix -- python dictionary mapping each character to an index.
    seed -- used for grading purposes. Do not worry about it.

    Returns:
    indices -- a list of length n containing the indices of the sampled characters.
    """
    
    # Retrieve parameters and relevant shapes from "parameters" dictionary
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    vocab_size = by.shape[0]
    n_a = Waa.shape[1]
    
    ### START CODE HERE ###
    # Step 1: Create the one-hot vector x for the first character (initializing the sequence generation). (≈1 line)
    x = np.zeros((vocab_size,1))
    # Step 1': Initialize a_prev as zeros (≈1 line)
    a_prev = np.zeros((n_a,1))
    
    # Create an empty list of indices, this is the list which will contain the list of indices of the characters to generate (≈1 line)
    indices = []
    
    # Idx is a flag to detect a newline character, we initialize it to -1
    idx = -1 
    
    # Loop over time-steps t. At each time-step, sample a character from a probability distribution and append 
    # its index to "indices". We'll stop if we reach 50 characters (which should be very unlikely with a well 
    # trained model), which helps debugging and prevents entering an infinite loop. 
    counter = 0
    newline_character = char_to_ix['\n']
    
    while (idx != newline_character and counter != 50):
        
        # Step 2: Forward propagate x using the equations (1), (2) and (3)
        a = np.tanh(np.dot(Wax,x)+np.dot(Waa,a_prev)+b)
        z = np.dot(Wya,a)+by
        y = softmax(z)
        
        # for grading purposes
        np.random.seed(counter+seed) 
        
        # Step 3: Sample the index of a character within the vocabulary from the probability distribution y
        idx = np.random.choice(range(len(y)),p=y.ravel())

        # Append the index to "indices"
        indices.append(idx)
        
        # Step 4: Overwrite the input character as the one corresponding to the sampled index.
        # 覆盖x，作为下个时间节点的输入，输入a中
        x = np.zeros((vocab_size,1))
        x[idx] = 1   #在字符代号向量中将对应字面的标号设置为1，如只有5个字符，则x[1]=1，array([[ 0.], [ 1.], [ 0.], [ 0.], [ 0.]])
       
        # Update "a_prev" to be "a"
        a_prev = a
        
        # for grading purposes
        seed += 1
        counter +=1
        
    ### END CODE HERE ###

    if (counter == 50):
        indices.append(char_to_ix['\n'])
    
    return indices

np.random.seed(2)
_, n_a = 20, 100
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}


indices = sample(parameters, char_to_ix, 0)
print("Sampling:")
print("list of sampled indices:", indices)
print("list of sampled characters:", [ix_to_char[i] for i in indices])

Sampling:
list of sampled indices: [12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 11, 5, 6, 12, 25, 0, 0]
list of sampled characters: ['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', 'k', 'e', 'f', 'l', 'y', '\n', '\n']

Expected output:

**list of sampled indices:**	[12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 11, 5, 6, 12, 25, 0, 0]
**list of sampled characters:**	['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', 'k', 'e', 'f', 'l', 'y', '\n', '\n']

3 - Building the language model

It is time to build the character-level language model for text generation.

3.1 - Gradient descent

In this section you will implement a function performing one step of stochastic gradient descent (with clipped gradients). You will go through the training examples one at a time, so the optimization algorithm will be stochastic gradient descent. As a reminder, here are the steps of a common optimization loop for an RNN:

• Forward propagate through the RNN to compute the loss
• Backward propagate through time to compute the gradients of the loss with respect to the parameters
• Clip the gradients if necessary
• Update your parameters using gradient descent

Exercise: Implement this optimization process (one step of stochastic gradient descent).

We provide you with the following functions:

def rnn_forward(X, Y, a_prev, parameters):
    """ Performs the forward propagation through the RNN and computes the cross-entropy loss.
    It returns the loss' value as well as a "cache" storing values to be used in the backpropagation."""
    ....
    return loss, cache
    
def rnn_backward(X, Y, parameters, cache):
    """ Performs the backward propagation through time to compute the gradients of the loss with respect
    to the parameters. It returns also all the hidden states."""
    ...
    return gradients, a

def update_parameters(parameters, gradients, learning_rate):
    """ Updates parameters using the Gradient Descent Update Rule."""
    ...
    return parameters

# GRADED FUNCTION: optimize

def optimize(X, Y, a_prev, parameters, learning_rate = 0.01):
    """
    Execute one step of the optimization to train the model.
    
    Arguments:
    X -- list of integers, where each integer is a number that maps to a character in the vocabulary.
    Y -- list of integers, exactly the same as X but shifted one index to the left.
    a_prev -- previous hidden state.
    parameters -- python dictionary containing:
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        b --  Bias, numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
    learning_rate -- learning rate for the model.
    
    Returns:
    loss -- value of the loss function (cross-entropy)
    gradients -- python dictionary containing:
                        dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
                        dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
                        dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)
                        db -- Gradients of bias vector, of shape (n_a, 1)
                        dby -- Gradients of output bias vector, of shape (n_y, 1)
    a[len(X)-1] -- the last hidden state, of shape (n_a, 1)
    """
    
    ### START CODE HERE ###
    
    # Forward propagate through time (≈1 line)
    loss, cache = rnn_forward(X,Y,a_prev,parameters)
    
    # Backpropagate through time (≈1 line)
    gradients, a = rnn_backward(X,Y,parameters,cache)
    
    # Clip your gradients between -5 (min) and 5 (max) (≈1 line)
    gradients = clip(gradients, 5)
    
    # Update parameters (≈1 line)
    parameters = update_parameters(parameters,gradients,learning_rate)
    
    ### END CODE HERE ###

    return loss, gradients, a[len(X)-1]

np.random.seed(1)
vocab_size, n_a = 27, 100
a_prev = np.random.randn(n_a, 1)
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
X = [12,3,5,11,22,3]
Y = [4,14,11,22,25, 26]

loss, gradients, a_last = optimize(X, Y, a_prev, parameters, learning_rate = 0.01)
print("Loss =", loss)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("np.argmax(gradients[\"dWax\"]) =", np.argmax(gradients["dWax"]))
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])
print("a_last[4] =", a_last[4])

Loss = 126.503975722
gradients["dWaa"][1][2] = 0.194709315347
np.argmax(gradients["dWax"]) = 93
gradients["dWya"][1][2] = -0.007773876032
gradients["db"][4] = [-0.06809825]
gradients["dby"][1] = [ 0.01538192]
a_last[4] = [-1.]

Expected output:

**Loss **	126.503975722
**gradients["dWaa"][1][2]**	0.194709315347
**np.argmax(gradients["dWax"])**	93
**gradients["dWya"][1][2]**	-0.007773876032
**gradients["db"][4]**	[-0.06809825]
**gradients["dby"][1]**	[ 0.01538192]
**a_last[4]**	[-1.]

3.2 - Training the model

Given the dataset of dinosaur names, we use each line of the dataset (one name) as one training example. Every 100 steps of stochastic gradient descent, you will sample 10 randomly chosen names to see how the algorithm is doing. Remember to shuffle the dataset, so that stochastic gradient descent visits the examples in random order.

Exercise: Follow the instructions and implement model(). When examples[index] contains one dinosaur name (string), to create an example (X, Y), you can use this:

        index = j % len(examples)
        X = [None] + [char_to_ix[ch] for ch in examples[index]] 
        Y = X[1:] + [char_to_ix["\n"]]

Note that we use: index= j % len(examples), where j = 1....num_iterations, to make sure that examples[index] is always a valid statement (index is smaller than len(examples)).
The first entry of X being None will be interpreted by rnn_forward() as setting $x^{⟨0⟩}=0$. Further, this ensures that Y is equal to X but shifted one step to the left, and with an additional “\n” appended to signify the end of the dinosaur name.

# GRADED FUNCTION: model

def model(data, ix_to_char, char_to_ix, num_iterations = 35000, n_a = 50, dino_names = 7, vocab_size = 27):
    """
    Trains the model and generates dinosaur names. 
    
    Arguments:
    data -- text corpus
    ix_to_char -- dictionary that maps the index to a character
    char_to_ix -- dictionary that maps a character to an index
    num_iterations -- number of iterations to train the model for
    n_a -- number of units of the RNN cell
    dino_names -- number of dinosaur names you want to sample at each iteration. 
    vocab_size -- number of unique characters found in the text, size of the vocabulary
    
    Returns:
    parameters -- learned parameters
    """
    
    # Retrieve n_x and n_y from vocab_size
    n_x, n_y = vocab_size, vocab_size
    
    # Initialize parameters
    parameters = initialize_parameters(n_a, n_x, n_y)
    
    # Initialize loss (this is required because we want to smooth our loss, don't worry about it)
    loss = get_initial_loss(vocab_size, dino_names)
    
    # Build list of all dinosaur names (training examples).
    with open("dinos.txt") as f:
        examples = f.readlines()
    examples = [x.lower().strip() for x in examples]
    
    # Shuffle list of all dinosaur names
    np.random.seed(0)
    np.random.shuffle(examples)
    
    # Initialize the hidden state of your LSTM
    a_prev = np.zeros((n_a, 1))
    
    # Optimization loop
    for j in range(num_iterations):
        
        ### START CODE HERE ###
        
        # Use the hint above to define one training example (X,Y) (≈ 2 lines)
        index = j % len(examples)
        X = [None] + [char_to_ix[ch] for ch in examples[index]]
        Y = X[1:]+[char_to_ix["\n"]]
        
        # Perform one optimization step: Forward-prop -> Backward-prop -> Clip -> Update parameters
        # Choose a learning rate of 0.01
        curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters, learning_rate = 0.01)
        
        ### END CODE HERE ###
        
        # Use a latency trick to keep the loss smooth. It happens here to accelerate the training.
        loss = smooth(loss, curr_loss)

        # Every 2000 Iteration, generate "n" characters thanks to sample() to check if the model is learning properly
        if j % 2000 == 0:
            
            print('Iteration: %d, Loss: %f' % (j, loss) + '\n')
            
            # The number of dinosaur names to print
            seed = 0
            for name in range(dino_names):
                
                # Sample indices and print them
                sampled_indices = sample(parameters, char_to_ix, seed)
                print_sample(sampled_indices, ix_to_char)
                
                seed += 1  # To get the same result for grading purposed, increment the seed by one. 
      
            print('\n')
        
    return parameters

Run the following cell, you should observe your model outputting random-looking characters at the first iteration. After a few thousand iterations, your model should learn to generate reasonable-looking names.

parameters = model(data, ix_to_char, char_to_ix)

Iteration: 0, Loss: 23.087336

Nkzxwtdmfqoeyhsqwasjkjvu
Kneb
Kzxwtdmfqoeyhsqwasjkjvu
Neb
Zxwtdmfqoeyhsqwasjkjvu
Eb
Xwtdmfqoeyhsqwasjkjvu


Iteration: 2000, Loss: 27.884160

Liusskeomnolxeros
Hmdaairus
Hytroligoraurus
Lecalosapaus
Xusicikoraurus
Abalpsamantisaurus
Tpraneronxeros


Iteration: 4000, Loss: 25.901815

Mivrosaurus
Inee
Ivtroplisaurus
Mbaaisaurus
Wusichisaurus
Cabaselachus
Toraperlethosdarenitochusthiamamumamaon


Iteration: 6000, Loss: 24.608779

Onwusceomosaurus
Lieeaerosaurus
Lxussaurus
Oma
Xusteonosaurus
Eeahosaurus
Toreonosaurus


Iteration: 8000, Loss: 24.070350

Onxusichepriuon
Kilabersaurus
Lutrodon
Omaaerosaurus
Xutrcheps
Edaksoje
Trodiktonus


Iteration: 10000, Loss: 23.844446

Onyusaurus
Klecalosaurus
Lustodon
Ola
Xusodonia
Eeaeosaurus
Troceosaurus


Iteration: 12000, Loss: 23.291971

Onyxosaurus
Kica
Lustrepiosaurus
Olaagrraiansaurus
Yuspangosaurus
Eealosaurus
Trognesaurus


Iteration: 14000, Loss: 23.382339

Meutromodromurus
Inda
Iutroinatorsaurus
Maca
Yusteratoptititan
Ca
Troclosaurus


Iteration: 16000, Loss: 23.288447

Meuspsangosaurus
Ingaa
Iusosaurus
Macalosaurus
Yushanis
Daalosaurus
Trpandon


Iteration: 18000, Loss: 22.823526

Phytrolonhonyg
Mela
Mustrerasaurus
Peg
Ytronorosaurus
Ehalosaurus
Trolomeehus


Iteration: 20000, Loss: 23.041871

Nousmofonosaurus
Loma
Lytrognatiasaurus
Ngaa
Ytroenetiaudostarmilus
Eiafosaurus
Troenchulunosaurus


Iteration: 22000, Loss: 22.728849

Piutyrangosaurus
Midaa
Myroranisaurus
Pedadosaurus
Ytrodon
Eiadosaurus
Trodoniomusitocorces


Iteration: 24000, Loss: 22.683403

Meutromeisaurus
Indeceratlapsaurus
Jurosaurus
Ndaa
Yusicheropterus
Eiaeropectus
Trodonasaurus


Iteration: 26000, Loss: 22.554523

Phyusaurus
Liceceron
Lyusichenodylus
Pegahus
Yustenhtonthosaurus
Elagosaurus
Trodontonsaurus


Iteration: 28000, Loss: 22.484472

Onyutimaerihus
Koia
Lytusaurus
Ola
Ytroheltorus
Eiadosaurus
Trofiashates


Iteration: 30000, Loss: 22.774404

Phytys
Lica
Lysus
Pacalosaurus
Ytrochisaurus
Eiacosaurus
Trochesaurus


Iteration: 32000, Loss: 22.209473

Mawusaurus
Jica
Lustoia
Macaisaurus
Yusolenqtesaurus
Eeaeosaurus
Trnanatrax


Iteration: 34000, Loss: 22.396744

Mavptokekus
Ilabaisaurus
Itosaurus
Macaesaurus
Yrosaurus
Eiaeosaurus
Trodon

Conclusion

You can see that your algorithm has started to generate plausible dinosaur names towards the end of the training. At first, it was generating random characters, but towards the end you could see dinosaur names with cool endings. Feel free to run the algorithm even longer and play with hyperparameters to see if you can get even better results. Our implemetation generated some really cool names like maconucon, marloralus and macingsersaurus. Your model hopefully also learned that dinosaur names tend to end in saurus, don, aura, tor, etc.

If your model generates some non-cool names, don’t blame the model entirely–not all actual dinosaur names sound cool. (For example, dromaeosauroides is an actual dinosaur name and is in the training set.) But this model should give you a set of candidates from which you can pick the coolest!

This assignment had used a relatively small dataset, so that you could train an RNN quickly on a CPU. Training a model of the english language requires a much bigger dataset, and usually needs much more computation, and could run for many hours on GPUs. We ran our dinosaur name for quite some time, and so far our favoriate name is the great, undefeatable, and fierce: Mangosaurus!

4 - Writing like Shakespeare

The rest of this notebook is optional and is not graded, but we hope you’ll do it anyway since it’s quite fun and informative.

A similar (but more complicated) task is to generate Shakespeare poems. Instead of learning from a dataset of Dinosaur names you can use a collection of Shakespearian poems. Using LSTM cells, you can learn longer term dependencies that span many characters in the text–e.g., where a character appearing somewhere a sequence can influence what should be a different character much much later in ths sequence. These long term dependencies were less important with dinosaur names, since the names were quite short.

Let’s become poets!
We have implemented a Shakespeare poem generator with Keras. Run the following cell to load the required packages and models. This may take a few minutes.

from __future__ import print_function
from keras.callbacks import LambdaCallback
from keras.models import Model, load_model, Sequential
from keras.layers import Dense, Activation, Dropout, Input, Masking
from keras.layers import LSTM
from keras.utils.data_utils import get_file
from keras.preprocessing.sequence import pad_sequences
from shakespeare_utils import *
import sys
import io

Loading text data...
Creating training set...
number of training examples: 31412
Vectorizing training set...
Loading model...

To save you some time, we have already trained a model for ~1000 epochs on a collection of Shakespearian poems called “The Sonnets”.

Let’s train the model for one more epoch. When it finishes training for an epoch—this will also take a few minutes—you can run generate_output, which will prompt asking you for an input (<40 characters). The poem will start with your sentence, and our RNN-Shakespeare will complete the rest of the poem for you! For example, try "Forsooth this maketh no sense " (don’t enter the quotation marks). Depending on whether you include the space at the end, your results might also differ–try it both ways, and try other inputs as well.

print_callback = LambdaCallback(on_epoch_end=on_epoch_end)

model.fit(x, y, batch_size=128, epochs=1, callbacks=[print_callback])

Epoch 1/1
31412/31412 [==============================] - 235s - loss: 2.5645   

# Run this cell to try with different inputs without having to re-train the model 
generate_output()

Write the beginning of your poem, the Shakespeare machine will complete it. Your input is: The world has kissed my soul


Here is your poem: 

The world has kissed my soul,
was ussored i yiins your fars dewert,
when hight ahele saull oft this, hage mune distrece.
but to ains forsw and more, and rest. to rrwadfeed,
drandion end, or som cond prond behuld ,the part chene
to live doth faest owntire my toosed dot,
as dorent belide thy kool limes not sood,
they lose frell own time your flest who glond,
no love out'nrels be a aleds and is fible
and him the alled my mer de

The RNN-Shakespeare model is very similar to the one you have built for dinosaur names. The only major differences are:

• LSTMs instead of the basic RNN to capture longer-range dependencies
• The model is a deeper, stacked LSTM model (2 layer)
• Using Keras instead of python to simplify the code

If you want to learn more, you can also check out the Keras Team’s text generation implementation on GitHub: https://github.com/keras-team/keras/blob/master/examples/lstm_text_generation.py.

Congratulations on finishing this notebook!

References:

• This exercise took inspiration from Andrej Karpathy’s implementation: https://gist.github.com/karpathy/d4dee566867f8291f086. To learn more about text generation, also check out Karpathy’s blog post.
• For the Shakespearian poem generator, our implementation was based on the implementation of an LSTM text generator by the Keras team: https://github.com/keras-team/keras/blob/master/examples/lstm_text_generation.py

---

Part 3

Improvise a Jazz Solo with an LSTM Network

Welcome to your final programming assignment of this week! In this notebook, you will implement a model that uses an LSTM to generate music. You will even be able to listen to your own music at the end of the assignment.

You will learn to:

• Apply an LSTM to music generation.
• Generate your own jazz music with deep learning.

Please run the following cell to load all the packages required in this assignment. This may take a few minutes.

from __future__ import print_function
import IPython
import sys
from music21 import *
import numpy as np
from grammar import *
from qa import *
from preprocess import * 
from music_utils import *
from data_utils import *
from keras.models import load_model, Model
from keras.layers import Dense, Activation, Dropout, Input, LSTM, Reshape, Lambda, RepeatVector
from keras.initializers import glorot_uniform
from keras.utils import to_categorical
from keras.optimizers import Adam
from keras import backend as K

1 - Problem statement

You would like to create a jazz music piece specially for a friend’s birthday. However, you don’t know any instruments or music composition. Fortunately, you know deep learning and will solve this problem using an LSTM netwok.

You will train a network to generate novel jazz solos in a style representative of a body of performed work.

1.1 - Dataset

You will train your algorithm on a corpus of Jazz music. Run the cell below to listen to a snippet of the audio from the training set:

IPython.display.Audio('./data/30s_seq.mp3')

没有数据集保存在自己电脑是听不到的，不过也不是特别重要，就是一段爵士乐
We have taken care of the preprocessing of the musical data to render it in terms of musical “values.” You can informally think of each “value” as a note, which comprises a pitch and a duration. For example, if you press down a specific piano key for 0.5 seconds, then you have just played a note. In music theory, a “value” is actually more complicated than this–specifically, it also captures the information needed to play multiple notes at the same time. For example, when playing a music piece, you might press down two piano keys at the same time (playng multiple notes at the same time generates what’s called a “chord”). But we don’t need to worry about the details of music theory for this assignment. For the purpose of this assignment, all you need to know is that we will obtain a dataset of values, and will learn an RNN model to generate sequences of values.

Our music generation system will use 78 unique values. Run the following code to load the raw music data and preprocess it into values. This might take a few minutes.

X, Y, n_values, indices_values = load_music_utils()
print('shape of X:', X.shape)
print('number of training examples:', X.shape[0])
print('Tx (length of sequence):', X.shape[1])
print('total # of unique values:', n_values)
print('Shape of Y:', Y.shape)

shape of X: (60, 30, 78)
number of training examples: 60
Tx (length of sequence): 30
total # of unique values: 78
Shape of Y: (30, 60, 78)

You have just loaded the following:

• X: This is an (m, $T_x$, 78) dimensional array. We have m training examples, each of which is a snippet of $T_x=30$ musical values. At each time step, the input is one of 78 different possible values, represented as a one-hot vector. Thus for example, X[i,t,:] is a one-hot vector representating the value of the i-th example at time t.

• Y: This is essentially the same as X, but shifted one step to the left (to the past). Similar to the dinosaurus assignment, we’re interested in the network using the previous values to predict the next value, so our sequence model will try to predict $y^{⟨t⟩}$ given $x^{⟨1⟩},\dots ,x^{⟨t⟩}$. However, the data in Y is reordered to be dimension $(T_y,m,78)$, where $T_y=T_x$. This format makes it more convenient to feed to the LSTM later.

• n_values: The number of unique values in this dataset. This should be 78.

• indices_values: python dictionary mapping from 0-77 to musical values.

1.2 - Overview of our model

Here is the architecture of the model we will use. This is similar to the Dinosaurus model you had used in the previous notebook, except that in you will be implementing it in Keras. The architecture is as follows:

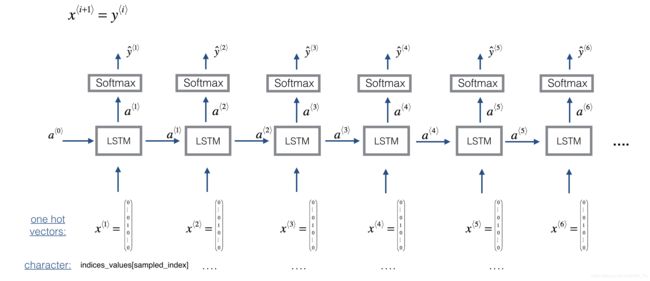
We will be training the model on random snippets of 30 values taken from a much longer piece of music. Thus, we won’t bother to set the first input $x^{⟨1⟩}=0$, which we had done previously to denote the start of a dinosaur name, since now most of these snippets of audio start somewhere in the middle of a piece of music. We are setting each of the snippts to have the same length $T_x=30$ to make vectorization easier.

2 - Building the model

In this part you will build and train a model that will learn musical patterns. To do so, you will need to build a model that takes in X of shape $(m,T_x,78)$ and Y of shape $(T_y,m,78)$. We will use an LSTM with 64 dimensional hidden states. Lets set n_a = 64.

n_a = 64 

Here’s how you can create a Keras model with multiple inputs and outputs. If you’re building an RNN where even at test time entire input sequence $x^{⟨1⟩},x^{⟨2⟩},\dots ,x^{⟨T_x⟩}$ were given in advance, for example if the inputs were words and the output was a label, then Keras has simple built-in functions to build the model. However, for sequence generation, at test time we don’t know all the values of $x^{⟨t⟩}$ in advance; instead we generate them one at a time using $x^{⟨t⟩}=y^{⟨t-1⟩}$. So the code will be a bit more complicated, and you’ll need to implement your own for-loop to iterate over the different time steps.

The function djmodel() will call the LSTM layer $T_x$ times using a for-loop, and it is important that all $T_x$ copies have the same weights. I.e., it should not re-initiaiize the weights every time—the $T_x$ steps should have shared weights. The key steps for implementing layers with shareable weights in Keras are:

1. Define the layer objects (we will use global variables for this).
2. Call these objects when propagating the input.

We have defined the layers objects you need as global variables. Please run the next cell to create them. Please check the Keras documentation to make sure you understand what these layers are: Reshape(), LSTM(), Dense().

reshapor = Reshape((1, 78))                        # Used in Step 2.B of djmodel(), below
LSTM_cell = LSTM(n_a, return_state = True)         # Used in Step 2.C  ，n_a是输出空间的维数
densor = Dense(n_values, activation='softmax')     # Used in Step 2.D ，输出的是一个（*，78）矩阵，上文提到n_values等于78

Each of reshapor, LSTM_cell and densor are now layer objects, and you can use them to implement djmodel(). In order to propagate a Keras tensor object X through one of these layers, use layer_object(X) (or layer_object([X,Y]) if it requires multiple inputs.). For example, reshapor(X) will propagate X through the Reshape((1,78)) layer defined above.

Exercise: Implement djmodel(). You will need to carry out 2 steps:

1. Create an empty list “outputs” to save the outputs of the LSTM Cell at every time step.

2. Loop for $t\in 1,\dots ,T_x$:

   A. Select the "t"th time-step vector from X. The shape of this selection should be (78,). To do so, create a custom Lambda layer in Keras by using this line of code:

           x = Lambda(lambda x: X[:,t,:])(X)

Look over the Keras documentation to figure out what this does. It is creating a “temporary” or “unnamed” function (that’s what Lambda functions are) that extracts out the appropriate one-hot vector, and making this function a Keras Layer object to apply to X.

B. Reshape x to be (1,78). You may find the reshapor() layer (defined below) helpful.

C. Run x through one step of LSTM_cell. Remember to initialize the LSTM_cell with the previous step’s hidden state $a$ and cell state $c$. Use the following formatting:

a, _, c = LSTM_cell(input_x, initial_state=[previous hidden state, previous cell state])

D. Propagate the LSTM’s output activation value through a dense+softmax layer using densor.

E. Append the predicted value to the list of “outputs”

# GRADED FUNCTION: djmodel

def djmodel(Tx, n_a, n_values):
    """
    Implement the model
    
    Arguments:
    Tx -- length of the sequence in a corpus
    n_a -- the number of activations used in our model
    n_values -- number of unique values in the music data 
    
    Returns:
    model -- a keras model with the 
    """
    
    # Define the input of your model with a shape 
    X = Input(shape=(Tx, n_values))
    
    # Define s0, initial hidden state for the decoder LSTM
    a0 = Input(shape=(n_a,), name='a0')
    c0 = Input(shape=(n_a,), name='c0')
    a = a0
    c = c0
    
    ### START CODE HERE ### 
    # Step 1: Create empty list to append the outputs while you iterate (≈1 line)
    outputs = []
    
    # Step 2: Loop
    for t in range(Tx):
        
        # Step 2.A: select the "t"th time step vector from X. 
        x = Lambda(lambda x: X[:,t,:])(X)
        # Step 2.B: Use reshapor to reshape x to be (1, n_values) (≈1 line)
        x = reshapor(x)
        # Step 2.C: Perform one step of the LSTM_cell
        a, _, c = LSTM_cell(x,initial_state=[a,c])
        # Step 2.D: Apply densor to the hidden state output of LSTM_Cell
        out = densor(a)
        # Step 2.E: add the output to "outputs"
        outputs.append(out)
        
    # Step 3: Create model instance
    model = Model(inputs=[X, a0, c0], outputs=outputs)
    
    ### END CODE HERE ###
    
    return model

Run the following cell to define your model. We will use Tx=30, n_a=64 (the dimension of the LSTM activations), and n_values=78. This cell may take a few seconds to run.

model = djmodel(Tx = 30 , n_a = 64, n_values = 78)

You now need to compile your model to be trained. We will Adam and a categorical cross-entropy loss.

opt = Adam(lr=0.01, beta_1=0.9, beta_2=0.999, decay=0.01)

model.compile(optimizer=opt, loss='categorical_crossentropy', metrics=['accuracy'])

Finally, lets initialize a0 and c0 for the LSTM’s initial state to be zero.

m = 60
a0 = np.zeros((m, n_a))
c0 = np.zeros((m, n_a))

Lets now fit the model! We will turn Y to a list before doing so, since the cost function expects Y to be provided in this format (one list item per time-step). So list(Y) is a list with 30 items, where each of the list items is of shape (60,78). Lets train for 100 epochs. This will take a few minutes.

model.fit([X, a0, c0], list(Y), epochs=100)

Epoch 1/100
60/60 [==============================] - 5s - loss: 125.7905 - dense_1_loss_1: 4.3548 - dense_1_loss_2: 4.3472 - dense_1_loss_3: 4.3400 - dense_1_loss_4: 4.3433 - dense_1_loss_5: 4.3349 - dense_1_loss_6: 4.3346 - dense_1_loss_7: 4.3402 - dense_1_loss_8: 4.3313 - dense_1_loss_9: 4.3375 - dense_1_loss_10: 4.3322 - dense_1_loss_11: 4.3341 - dense_1_loss_12: 4.3402 - dense_1_loss_13: 4.3327 - dense_1_loss_14: 4.3308 - dense_1_loss_15: 4.3387 - dense_1_loss_16: 4.3276 - dense_1_loss_17: 4.3387 - dense_1_loss_18: 4.3402 - dense_1_loss_19: 4.3380 - dense_1_loss_20: 4.3403 - dense_1_loss_21: 4.3429 - dense_1_loss_22: 4.3335 - dense_1_loss_23: 4.3367 - dense_1_loss_24: 4.3292 - dense_1_loss_25: 4.3416 - dense_1_loss_26: 4.3374 - dense_1_loss_27: 4.3364 - dense_1_loss_28: 4.3379 - dense_1_loss_29: 4.3374 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0167 - dense_1_acc_2: 0.0333 - dense_1_acc_3: 0.0833 - dense_1_acc_4: 0.0833 - dense_1_acc_5: 0.1000 - dense_1_acc_6: 0.1333 - dense_1_acc_7: 0.0333 - dense_1_acc_8: 0.1500 - dense_1_acc_9: 0.0500 - dense_1_acc_10: 0.1000 - dense_1_acc_11: 0.0500 - dense_1_acc_12: 0.0500 - dense_1_acc_13: 0.0500 - dense_1_acc_14: 0.0833 - dense_1_acc_15: 0.1000 - dense_1_acc_16: 0.0667 - dense_1_acc_17: 0.0667 - dense_1_acc_18: 0.0167 - dense_1_acc_19: 0.1000 - dense_1_acc_20: 0.0500 - dense_1_acc_21: 0.0333 - dense_1_acc_22: 0.1167 - dense_1_acc_23: 0.0667 - dense_1_acc_24: 0.1000 - dense_1_acc_25: 0.0500 - dense_1_acc_26: 0.1000 - dense_1_acc_27: 0.0333 - dense_1_acc_28: 0.0833 - dense_1_acc_29: 0.0833 - dense_1_acc_30: 0.0000e+00                                                                                 
Epoch 2/100
60/60 [==============================] - 0s - loss: 122.2474 - dense_1_loss_1: 4.3323 - dense_1_loss_2: 4.3020 - dense_1_loss_3: 4.2734 - dense_1_loss_4: 4.2752 - dense_1_loss_5: 4.2400 - dense_1_loss_6: 4.2495 - dense_1_loss_7: 4.2429 - dense_1_loss_8: 4.2165 - dense_1_loss_9: 4.2240 - dense_1_loss_10: 4.2050 - dense_1_loss_11: 4.1955 - dense_1_loss_12: 4.2388 - dense_1_loss_13: 4.2028 - dense_1_loss_14: 4.1770 - dense_1_loss_15: 4.2080 - dense_1_loss_16: 4.1906 - dense_1_loss_17: 4.1753 - dense_1_loss_18: 4.2276 - dense_1_loss_19: 4.1828 - dense_1_loss_20: 4.1918 - dense_1_loss_21: 4.1976 - dense_1_loss_22: 4.1874 - dense_1_loss_23: 4.1971 - dense_1_loss_24: 4.2015 - dense_1_loss_25: 4.2216 - dense_1_loss_26: 4.1518 - dense_1_loss_27: 4.1891 - dense_1_loss_28: 4.1745 - dense_1_loss_29: 4.1756 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.2167 - dense_1_acc_3: 0.2000 - dense_1_acc_4: 0.1500 - dense_1_acc_5: 0.2333 - dense_1_acc_6: 0.1833 - dense_1_acc_7: 0.1333 - dense_1_acc_8: 0.2667 - dense_1_acc_9: 0.2167 - dense_1_acc_10: 0.2000 - dense_1_acc_11: 0.1500 - dense_1_acc_12: 0.1000 - dense_1_acc_13: 0.1833 - dense_1_acc_14: 0.1833 - dense_1_acc_15: 0.1167 - dense_1_acc_16: 0.1667 - dense_1_acc_17: 0.2167 - dense_1_acc_18: 0.1167 - dense_1_acc_19: 0.1833 - dense_1_acc_20: 0.2000 - dense_1_acc_21: 0.1167 - dense_1_acc_22: 0.1167 - dense_1_acc_23: 0.1000 - dense_1_acc_24: 0.0833 - dense_1_acc_25: 0.1167 - dense_1_acc_26: 0.2167 - dense_1_acc_27: 0.0500 - dense_1_acc_28: 0.1500 - dense_1_acc_29: 0.1500 - dense_1_acc_30: 0.0000e+00     
Epoch 3/100
60/60 [==============================] - 0s - loss: 116.1832 - dense_1_loss_1: 4.3103 - dense_1_loss_2: 4.2524 - dense_1_loss_3: 4.1878 - dense_1_loss_4: 4.1766 - dense_1_loss_5: 4.1136 - dense_1_loss_6: 4.1241 - dense_1_loss_7: 4.0809 - dense_1_loss_8: 3.9841 - dense_1_loss_9: 3.9638 - dense_1_loss_10: 3.8799 - dense_1_loss_11: 3.8546 - dense_1_loss_12: 4.0772 - dense_1_loss_13: 3.9107 - dense_1_loss_14: 3.8774 - dense_1_loss_15: 3.9733 - dense_1_loss_16: 3.9725 - dense_1_loss_17: 3.9689 - dense_1_loss_18: 4.1250 - dense_1_loss_19: 3.9007 - dense_1_loss_20: 3.9822 - dense_1_loss_21: 3.9722 - dense_1_loss_22: 3.9978 - dense_1_loss_23: 3.8809 - dense_1_loss_24: 3.9328 - dense_1_loss_25: 4.1316 - dense_1_loss_26: 3.7695 - dense_1_loss_27: 3.8546 - dense_1_loss_28: 3.9165 - dense_1_loss_29: 4.0113 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.2167 - dense_1_acc_3: 0.2000 - dense_1_acc_4: 0.1333 - dense_1_acc_5: 0.2167 - dense_1_acc_6: 0.1333 - dense_1_acc_7: 0.1000 - dense_1_acc_8: 0.2167 - dense_1_acc_9: 0.1333 - dense_1_acc_10: 0.1333 - dense_1_acc_11: 0.0500 - dense_1_acc_12: 0.0500 - dense_1_acc_13: 0.0667 - dense_1_acc_14: 0.0833 - dense_1_acc_15: 0.0833 - dense_1_acc_16: 0.1000 - dense_1_acc_17: 0.1333 - dense_1_acc_18: 0.0500 - dense_1_acc_19: 0.0833 - dense_1_acc_20: 0.1000 - dense_1_acc_21: 0.1000 - dense_1_acc_22: 0.0167 - dense_1_acc_23: 0.0667 - dense_1_acc_24: 0.0833 - dense_1_acc_25: 0.0333 - dense_1_acc_26: 0.1500 - dense_1_acc_27: 0.0833 - dense_1_acc_28: 0.0833 - dense_1_acc_29: 0.0833 - dense_1_acc_30: 0.0000e+00         
Epoch 4/100
60/60 [==============================] - 0s - loss: 112.0846 - dense_1_loss_1: 4.2890 - dense_1_loss_2: 4.2047 - dense_1_loss_3: 4.0946 - dense_1_loss_4: 4.0756 - dense_1_loss_5: 3.9635 - dense_1_loss_6: 3.9867 - dense_1_loss_7: 3.9128 - dense_1_loss_8: 3.6999 - dense_1_loss_9: 3.7927 - dense_1_loss_10: 3.6339 - dense_1_loss_11: 3.7210 - dense_1_loss_12: 3.9820 - dense_1_loss_13: 3.7396 - dense_1_loss_14: 3.6741 - dense_1_loss_15: 3.7550 - dense_1_loss_16: 3.8392 - dense_1_loss_17: 3.8953 - dense_1_loss_18: 3.9264 - dense_1_loss_19: 3.6811 - dense_1_loss_20: 3.9559 - dense_1_loss_21: 3.9265 - dense_1_loss_22: 3.8323 - dense_1_loss_23: 3.8044 - dense_1_loss_24: 3.7063 - dense_1_loss_25: 3.9283 - dense_1_loss_26: 3.5847 - dense_1_loss_27: 3.7196 - dense_1_loss_28: 3.8434 - dense_1_loss_29: 3.9162 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0833 - dense_1_acc_2: 0.1667 - dense_1_acc_3: 0.1667 - dense_1_acc_4: 0.1333 - dense_1_acc_5: 0.2167 - dense_1_acc_6: 0.1333 - dense_1_acc_7: 0.1000 - dense_1_acc_8: 0.1500 - dense_1_acc_9: 0.1667 - dense_1_acc_10: 0.1500 - dense_1_acc_11: 0.1167 - dense_1_acc_12: 0.0667 - dense_1_acc_13: 0.1167 - dense_1_acc_14: 0.1500 - dense_1_acc_15: 0.0833 - dense_1_acc_16: 0.1333 - dense_1_acc_17: 0.1500 - dense_1_acc_18: 0.0667 - dense_1_acc_19: 0.0833 - dense_1_acc_20: 0.0667 - dense_1_acc_21: 0.0667 - dense_1_acc_22: 0.1000 - dense_1_acc_23: 0.0667 - dense_1_acc_24: 0.0500 - dense_1_acc_25: 0.1000 - dense_1_acc_26: 0.1167 - dense_1_acc_27: 0.0500 - dense_1_acc_28: 0.1333 - dense_1_acc_29: 0.1333 - dense_1_acc_30: 0.0000e+00         
Epoch 5/100
60/60 [==============================] - 0s - loss: 109.9746 - dense_1_loss_1: 4.2701 - dense_1_loss_2: 4.1569 - dense_1_loss_3: 4.0147 - dense_1_loss_4: 3.9888 - dense_1_loss_5: 3.8441 - dense_1_loss_6: 3.8960 - dense_1_loss_7: 3.8208 - dense_1_loss_8: 3.5740 - dense_1_loss_9: 3.7188 - dense_1_loss_10: 3.5308 - dense_1_loss_11: 3.6513 - dense_1_loss_12: 3.9175 - dense_1_loss_13: 3.6169 - dense_1_loss_14: 3.5620 - dense_1_loss_15: 3.6720 - dense_1_loss_16: 3.7250 - dense_1_loss_17: 3.7640 - dense_1_loss_18: 3.7901 - dense_1_loss_19: 3.5713 - dense_1_loss_20: 3.9400 - dense_1_loss_21: 3.9333 - dense_1_loss_22: 3.7557 - dense_1_loss_23: 3.6897 - dense_1_loss_24: 3.6607 - dense_1_loss_25: 3.8833 - dense_1_loss_26: 3.5603 - dense_1_loss_27: 3.6881 - dense_1_loss_28: 3.8326 - dense_1_loss_29: 3.9460 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.1000 - dense_1_acc_2: 0.1333 - dense_1_acc_3: 0.1833 - dense_1_acc_4: 0.1667 - dense_1_acc_5: 0.2167 - dense_1_acc_6: 0.1000 - dense_1_acc_7: 0.0833 - dense_1_acc_8: 0.1833 - dense_1_acc_9: 0.1333 - dense_1_acc_10: 0.1167 - dense_1_acc_11: 0.1500 - dense_1_acc_12: 0.0833 - dense_1_acc_13: 0.1667 - dense_1_acc_14: 0.1833 - dense_1_acc_15: 0.1667 - dense_1_acc_16: 0.1000 - dense_1_acc_17: 0.1500 - dense_1_acc_18: 0.1167 - dense_1_acc_19: 0.1500 - dense_1_acc_20: 0.0500 - dense_1_acc_21: 0.0333 - dense_1_acc_22: 0.1833 - dense_1_acc_23: 0.1333 - dense_1_acc_24: 0.1167 - dense_1_acc_25: 0.0667 - dense_1_acc_26: 0.1167 - dense_1_acc_27: 0.1000 - dense_1_acc_28: 0.1500 - dense_1_acc_29: 0.0667 - dense_1_acc_30: 0.0000e+00         
Epoch 6/100

60/60 [==============================] - 0s - loss: 107.2252 - dense_1_loss_1: 4.2555 - dense_1_loss_2: 4.1194 - dense_1_loss_3: 3.9438 - dense_1_loss_4: 3.9241 - dense_1_loss_5: 3.7648 - dense_1_loss_6: 3.8160 - dense_1_loss_7: 3.7725 - dense_1_loss_8: 3.4905 - dense_1_loss_9: 3.6262 - dense_1_loss_10: 3.4600 - dense_1_loss_11: 3.5579 - dense_1_loss_12: 3.7701 - dense_1_loss_13: 3.4956 - dense_1_loss_14: 3.4211 - dense_1_loss_15: 3.5689 - dense_1_loss_16: 3.5720 - dense_1_loss_17: 3.6144 - dense_1_loss_18: 3.6750 - dense_1_loss_19: 3.4315 - dense_1_loss_20: 3.8297 - dense_1_loss_21: 3.8063 - dense_1_loss_22: 3.6358 - dense_1_loss_23: 3.7487 - dense_1_loss_24: 3.6094 - dense_1_loss_25: 3.7081 - dense_1_loss_26: 3.5019 - dense_1_loss_27: 3.6086 - dense_1_loss_28: 3.7027 - dense_1_loss_29: 3.7945 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.1000 - dense_1_acc_2: 0.1500 - dense_1_acc_3: 0.2000 - dense_1_acc_4: 0.1667 - dense_1_acc_5: 0.2167 - dense_1_acc_6: 0.0833 - dense_1_acc_7: 0.1000 - dense_1_acc_8: 0.1833 - dense_1_acc_9: 0.1333 - dense_1_acc_10: 0.1333 - dense_1_acc_11: 0.1500 - dense_1_acc_12: 0.1000 - dense_1_acc_13: 0.2333 - dense_1_acc_14: 0.1833 - dense_1_acc_15: 0.1167 - dense_1_acc_16: 0.1333 - dense_1_acc_17: 0.1833 - dense_1_acc_18: 0.1500 - dense_1_acc_19: 0.1667 - dense_1_acc_20: 0.1000 - dense_1_acc_21: 0.1000 - dense_1_acc_22: 0.1667 - dense_1_acc_23: 0.0333 - dense_1_acc_24: 0.0667 - dense_1_acc_25: 0.1167 - dense_1_acc_26: 0.1333 - dense_1_acc_27: 0.0667 - dense_1_acc_28: 0.1667 - dense_1_acc_29: 0.1333 - dense_1_acc_30: 0.0000e+00     
Epoch 7/100
60/60 [==============================] - 0s - loss: 103.6165 - dense_1_loss_1: 4.2409 - dense_1_loss_2: 4.0803 - dense_1_loss_3: 3.8774 - dense_1_loss_4: 3.8608 - dense_1_loss_5: 3.6721 - dense_1_loss_6: 3.7321 - dense_1_loss_7: 3.7056 - dense_1_loss_8: 3.4034 - dense_1_loss_9: 3.4969 - dense_1_loss_10: 3.3006 - dense_1_loss_11: 3.4533 - dense_1_loss_12: 3.6369 - dense_1_loss_13: 3.3209 - dense_1_loss_14: 3.3176 - dense_1_loss_15: 3.4912 - dense_1_loss_16: 3.3754 - dense_1_loss_17: 3.5055 - dense_1_loss_18: 3.5528 - dense_1_loss_19: 3.3782 - dense_1_loss_20: 3.6400 - dense_1_loss_21: 3.6227 - dense_1_loss_22: 3.5647 - dense_1_loss_23: 3.5530 - dense_1_loss_24: 3.3728 - dense_1_loss_25: 3.6239 - dense_1_loss_26: 3.3192 - dense_1_loss_27: 3.4105 - dense_1_loss_28: 3.4766 - dense_1_loss_29: 3.6312 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.1000 - dense_1_acc_2: 0.1833 - dense_1_acc_3: 0.1833 - dense_1_acc_4: 0.1500 - dense_1_acc_5: 0.2167 - dense_1_acc_6: 0.1000 - dense_1_acc_7: 0.1167 - dense_1_acc_8: 0.2167 - dense_1_acc_9: 0.1333 - dense_1_acc_10: 0.1500 - dense_1_acc_11: 0.1333 - dense_1_acc_12: 0.1000 - dense_1_acc_13: 0.2500 - dense_1_acc_14: 0.2000 - dense_1_acc_15: 0.1167 - dense_1_acc_16: 0.2333 - dense_1_acc_17: 0.2333 - dense_1_acc_18: 0.1000 - dense_1_acc_19: 0.1833 - dense_1_acc_20: 0.1333 - dense_1_acc_21: 0.1333 - dense_1_acc_22: 0.0833 - dense_1_acc_23: 0.1333 - dense_1_acc_24: 0.1167 - dense_1_acc_25: 0.1000 - dense_1_acc_26: 0.1833 - dense_1_acc_27: 0.1333 - dense_1_acc_28: 0.1667 - dense_1_acc_29: 0.1500 - dense_1_acc_30: 0.0000e+00     
Epoch 8/100
60/60 [==============================] - 0s - loss: 100.2986 - dense_1_loss_1: 4.2285 - dense_1_loss_2: 4.0390 - dense_1_loss_3: 3.8121 - dense_1_loss_4: 3.7879 - dense_1_loss_5: 3.5739 - dense_1_loss_6: 3.6278 - dense_1_loss_7: 3.6090 - dense_1_loss_8: 3.2866 - dense_1_loss_9: 3.3970 - dense_1_loss_10: 3.1910 - dense_1_loss_11: 3.3464 - dense_1_loss_12: 3.5250 - dense_1_loss_13: 3.2183 - dense_1_loss_14: 3.1799 - dense_1_loss_15: 3.3503 - dense_1_loss_16: 3.2614 - dense_1_loss_17: 3.3380 - dense_1_loss_18: 3.4039 - dense_1_loss_19: 3.2988 - dense_1_loss_20: 3.4986 - dense_1_loss_21: 3.5015 - dense_1_loss_22: 3.4135 - dense_1_loss_23: 3.4343 - dense_1_loss_24: 3.2744 - dense_1_loss_25: 3.4204 - dense_1_loss_26: 3.1444 - dense_1_loss_27: 3.2632 - dense_1_loss_28: 3.3899 - dense_1_loss_29: 3.4837 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.1000 - dense_1_acc_2: 0.2167 - dense_1_acc_3: 0.2000 - dense_1_acc_4: 0.1667 - dense_1_acc_5: 0.2167 - dense_1_acc_6: 0.1500 - dense_1_acc_7: 0.1167 - dense_1_acc_8: 0.2500 - dense_1_acc_9: 0.1667 - dense_1_acc_10: 0.1667 - dense_1_acc_11: 0.1667 - dense_1_acc_12: 0.1667 - dense_1_acc_13: 0.2500 - dense_1_acc_14: 0.2167 - dense_1_acc_15: 0.1333 - dense_1_acc_16: 0.1833 - dense_1_acc_17: 0.2333 - dense_1_acc_18: 0.1500 - dense_1_acc_19: 0.1833 - dense_1_acc_20: 0.1667 - dense_1_acc_21: 0.1667 - dense_1_acc_22: 0.1333 - dense_1_acc_23: 0.0833 - dense_1_acc_24: 0.0833 - dense_1_acc_25: 0.1500 - dense_1_acc_26: 0.2500 - dense_1_acc_27: 0.1833 - dense_1_acc_28: 0.1333 - dense_1_acc_29: 0.1500 - dense_1_acc_30: 0.0000e+00     
Epoch 9/100
60/60 [==============================] - 0s - loss: 96.4867 - dense_1_loss_1: 4.2171 - dense_1_loss_2: 4.0011 - dense_1_loss_3: 3.7456 - dense_1_loss_4: 3.7135 - dense_1_loss_5: 3.4670 - dense_1_loss_6: 3.5261 - dense_1_loss_7: 3.5063 - dense_1_loss_8: 3.1717 - dense_1_loss_9: 3.2660 - dense_1_loss_10: 3.0199 - dense_1_loss_11: 3.2227 - dense_1_loss_12: 3.3843 - dense_1_loss_13: 3.0338 - dense_1_loss_14: 3.0232 - dense_1_loss_15: 3.2289 - dense_1_loss_16: 3.1369 - dense_1_loss_17: 3.1498 - dense_1_loss_18: 3.3283 - dense_1_loss_19: 3.0828 - dense_1_loss_20: 3.3032 - dense_1_loss_21: 3.3288 - dense_1_loss_22: 3.2761 - dense_1_loss_23: 3.3236 - dense_1_loss_24: 3.1123 - dense_1_loss_25: 3.2789 - dense_1_loss_26: 3.0485 - dense_1_loss_27: 3.2005 - dense_1_loss_28: 3.1416 - dense_1_loss_29: 3.2482 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.1000 - dense_1_acc_2: 0.2167 - dense_1_acc_3: 0.2000 - dense_1_acc_4: 0.1667 - dense_1_acc_5: 0.2333 - dense_1_acc_6: 0.1500 - dense_1_acc_7: 0.1333 - dense_1_acc_8: 0.2167 - dense_1_acc_9: 0.1500 - dense_1_acc_10: 0.1833 - dense_1_acc_11: 0.1667 - dense_1_acc_12: 0.1167 - dense_1_acc_13: 0.2667 - dense_1_acc_14: 0.2667 - dense_1_acc_15: 0.1167 - dense_1_acc_16: 0.1833 - dense_1_acc_17: 0.2500 - dense_1_acc_18: 0.1333 - dense_1_acc_19: 0.1833 - dense_1_acc_20: 0.1500 - dense_1_acc_21: 0.1500 - dense_1_acc_22: 0.1500 - dense_1_acc_23: 0.1333 - dense_1_acc_24: 0.1167 - dense_1_acc_25: 0.1500 - dense_1_acc_26: 0.2167 - dense_1_acc_27: 0.1167 - dense_1_acc_28: 0.2000 - dense_1_acc_29: 0.1500 - dense_1_acc_30: 0.0000e+00     
Epoch 10/100
60/60 [==============================] - 0s - loss: 92.1036 - dense_1_loss_1: 4.2055 - dense_1_loss_2: 3.9599 - dense_1_loss_3: 3.6736 - dense_1_loss_4: 3.6252 - dense_1_loss_5: 3.3441 - dense_1_loss_6: 3.3914 - dense_1_loss_7: 3.3717 - dense_1_loss_8: 3.0158 - dense_1_loss_9: 3.1188 - dense_1_loss_10: 2.8667 - dense_1_loss_11: 3.1087 - dense_1_loss_12: 3.1996 - dense_1_loss_13: 2.8952 - dense_1_loss_14: 2.8452 - dense_1_loss_15: 3.0069 - dense_1_loss_16: 3.0392 - dense_1_loss_17: 2.9957 - dense_1_loss_18: 3.1535 - dense_1_loss_19: 2.9384 - dense_1_loss_20: 3.1164 - dense_1_loss_21: 3.1241 - dense_1_loss_22: 3.1637 - dense_1_loss_23: 3.1025 - dense_1_loss_24: 2.9117 - dense_1_loss_25: 3.0509 - dense_1_loss_26: 2.8022 - dense_1_loss_27: 3.0509 - dense_1_loss_28: 2.9774 - dense_1_loss_29: 3.0487 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.2333 - dense_1_acc_3: 0.2000 - dense_1_acc_4: 0.1667 - dense_1_acc_5: 0.2333 - dense_1_acc_6: 0.1500 - dense_1_acc_7: 0.1333 - dense_1_acc_8: 0.2500 - dense_1_acc_9: 0.1667 - dense_1_acc_10: 0.2167 - dense_1_acc_11: 0.2500 - dense_1_acc_12: 0.1500 - dense_1_acc_13: 0.2167 - dense_1_acc_14: 0.2500 - dense_1_acc_15: 0.2333 - dense_1_acc_16: 0.1833 - dense_1_acc_17: 0.2833 - dense_1_acc_18: 0.2000 - dense_1_acc_19: 0.2500 - dense_1_acc_20: 0.1667 - dense_1_acc_21: 0.1833 - dense_1_acc_22: 0.1667 - dense_1_acc_23: 0.1667 - dense_1_acc_24: 0.1500 - dense_1_acc_25: 0.1833 - dense_1_acc_26: 0.2667 - dense_1_acc_27: 0.1833 - dense_1_acc_28: 0.2333 - dense_1_acc_29: 0.2000 - dense_1_acc_30: 0.0000e+00     
Epoch 11/100

60/60 [==============================] - 0s - loss: 87.4204 - dense_1_loss_1: 4.1957 - dense_1_loss_2: 3.9202 - dense_1_loss_3: 3.6029 - dense_1_loss_4: 3.5319 - dense_1_loss_5: 3.2218 - dense_1_loss_6: 3.2450 - dense_1_loss_7: 3.2034 - dense_1_loss_8: 2.8467 - dense_1_loss_9: 2.9870 - dense_1_loss_10: 2.6888 - dense_1_loss_11: 2.9767 - dense_1_loss_12: 2.9718 - dense_1_loss_13: 2.6785 - dense_1_loss_14: 2.6365 - dense_1_loss_15: 2.8062 - dense_1_loss_16: 2.8875 - dense_1_loss_17: 2.7918 - dense_1_loss_18: 2.9988 - dense_1_loss_19: 2.7724 - dense_1_loss_20: 2.9019 - dense_1_loss_21: 2.8370 - dense_1_loss_22: 2.9532 - dense_1_loss_23: 2.9555 - dense_1_loss_24: 2.7163 - dense_1_loss_25: 2.8898 - dense_1_loss_26: 2.6431 - dense_1_loss_27: 2.8576 - dense_1_loss_28: 2.8309 - dense_1_loss_29: 2.8714 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.2833 - dense_1_acc_3: 0.2500 - dense_1_acc_4: 0.1833 - dense_1_acc_5: 0.2500 - dense_1_acc_6: 0.1500 - dense_1_acc_7: 0.1833 - dense_1_acc_8: 0.2667 - dense_1_acc_9: 0.1667 - dense_1_acc_10: 0.2667 - dense_1_acc_11: 0.1833 - dense_1_acc_12: 0.1833 - dense_1_acc_13: 0.2667 - dense_1_acc_14: 0.2500 - dense_1_acc_15: 0.2333 - dense_1_acc_16: 0.2500 - dense_1_acc_17: 0.3000 - dense_1_acc_18: 0.1833 - dense_1_acc_19: 0.2833 - dense_1_acc_20: 0.2500 - dense_1_acc_21: 0.2167 - dense_1_acc_22: 0.1333 - dense_1_acc_23: 0.2000 - dense_1_acc_24: 0.2167 - dense_1_acc_25: 0.2167 - dense_1_acc_26: 0.3333 - dense_1_acc_27: 0.2500 - dense_1_acc_28: 0.2167 - dense_1_acc_29: 0.2333 - dense_1_acc_30: 0.0000e+00     
Epoch 12/100
60/60 [==============================] - 0s - loss: 82.9246 - dense_1_loss_1: 4.1863 - dense_1_loss_2: 3.8804 - dense_1_loss_3: 3.5337 - dense_1_loss_4: 3.4316 - dense_1_loss_5: 3.1077 - dense_1_loss_6: 3.0858 - dense_1_loss_7: 3.0520 - dense_1_loss_8: 2.6794 - dense_1_loss_9: 2.8422 - dense_1_loss_10: 2.5442 - dense_1_loss_11: 2.8835 - dense_1_loss_12: 2.7807 - dense_1_loss_13: 2.4584 - dense_1_loss_14: 2.4761 - dense_1_loss_15: 2.6497 - dense_1_loss_16: 2.7594 - dense_1_loss_17: 2.5839 - dense_1_loss_18: 2.8318 - dense_1_loss_19: 2.5962 - dense_1_loss_20: 2.7299 - dense_1_loss_21: 2.6396 - dense_1_loss_22: 2.7816 - dense_1_loss_23: 2.7179 - dense_1_loss_24: 2.5766 - dense_1_loss_25: 2.6919 - dense_1_loss_26: 2.4942 - dense_1_loss_27: 2.6611 - dense_1_loss_28: 2.6318 - dense_1_loss_29: 2.6371 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3167 - dense_1_acc_3: 0.2500 - dense_1_acc_4: 0.2000 - dense_1_acc_5: 0.2500 - dense_1_acc_6: 0.1500 - dense_1_acc_7: 0.2500 - dense_1_acc_8: 0.2833 - dense_1_acc_9: 0.2000 - dense_1_acc_10: 0.2833 - dense_1_acc_11: 0.1667 - dense_1_acc_12: 0.1667 - dense_1_acc_13: 0.3167 - dense_1_acc_14: 0.3000 - dense_1_acc_15: 0.2500 - dense_1_acc_16: 0.2667 - dense_1_acc_17: 0.3167 - dense_1_acc_18: 0.1833 - dense_1_acc_19: 0.2667 - dense_1_acc_20: 0.2500 - dense_1_acc_21: 0.2500 - dense_1_acc_22: 0.1500 - dense_1_acc_23: 0.2167 - dense_1_acc_24: 0.2167 - dense_1_acc_25: 0.1833 - dense_1_acc_26: 0.3333 - dense_1_acc_27: 0.2667 - dense_1_acc_28: 0.2667 - dense_1_acc_29: 0.2833 - dense_1_acc_30: 0.0000e+00     
Epoch 13/100
60/60 [==============================] - 0s - loss: 79.3931 - dense_1_loss_1: 4.1777 - dense_1_loss_2: 3.8428 - dense_1_loss_3: 3.4657 - dense_1_loss_4: 3.3253 - dense_1_loss_5: 2.9852 - dense_1_loss_6: 2.9147 - dense_1_loss_7: 2.8603 - dense_1_loss_8: 2.5470 - dense_1_loss_9: 2.6973 - dense_1_loss_10: 2.4604 - dense_1_loss_11: 2.7313 - dense_1_loss_12: 2.6875 - dense_1_loss_13: 2.2754 - dense_1_loss_14: 2.3103 - dense_1_loss_15: 2.5479 - dense_1_loss_16: 2.6414 - dense_1_loss_17: 2.4352 - dense_1_loss_18: 2.6365 - dense_1_loss_19: 2.4702 - dense_1_loss_20: 2.6079 - dense_1_loss_21: 2.5095 - dense_1_loss_22: 2.6129 - dense_1_loss_23: 2.5523 - dense_1_loss_24: 2.4086 - dense_1_loss_25: 2.5659 - dense_1_loss_26: 2.4876 - dense_1_loss_27: 2.6006 - dense_1_loss_28: 2.5410 - dense_1_loss_29: 2.4945 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3000 - dense_1_acc_3: 0.2667 - dense_1_acc_4: 0.2000 - dense_1_acc_5: 0.2667 - dense_1_acc_6: 0.2333 - dense_1_acc_7: 0.3333 - dense_1_acc_8: 0.3667 - dense_1_acc_9: 0.2167 - dense_1_acc_10: 0.3167 - dense_1_acc_11: 0.2167 - dense_1_acc_12: 0.1667 - dense_1_acc_13: 0.3833 - dense_1_acc_14: 0.3167 - dense_1_acc_15: 0.2833 - dense_1_acc_16: 0.1500 - dense_1_acc_17: 0.3167 - dense_1_acc_18: 0.2500 - dense_1_acc_19: 0.2500 - dense_1_acc_20: 0.2833 - dense_1_acc_21: 0.2667 - dense_1_acc_22: 0.1833 - dense_1_acc_23: 0.2333 - dense_1_acc_24: 0.3000 - dense_1_acc_25: 0.2167 - dense_1_acc_26: 0.2833 - dense_1_acc_27: 0.2167 - dense_1_acc_28: 0.2667 - dense_1_acc_29: 0.2500 - dense_1_acc_30: 0.0000e+00     
Epoch 14/100
60/60 [==============================] - 0s - loss: 74.5886 - dense_1_loss_1: 4.1705 - dense_1_loss_2: 3.8017 - dense_1_loss_3: 3.3942 - dense_1_loss_4: 3.2162 - dense_1_loss_5: 2.8692 - dense_1_loss_6: 2.7544 - dense_1_loss_7: 2.7227 - dense_1_loss_8: 2.3930 - dense_1_loss_9: 2.5169 - dense_1_loss_10: 2.3029 - dense_1_loss_11: 2.5167 - dense_1_loss_12: 2.4631 - dense_1_loss_13: 2.1543 - dense_1_loss_14: 2.2057 - dense_1_loss_15: 2.3045 - dense_1_loss_16: 2.4395 - dense_1_loss_17: 2.2148 - dense_1_loss_18: 2.3700 - dense_1_loss_19: 2.3109 - dense_1_loss_20: 2.4442 - dense_1_loss_21: 2.2790 - dense_1_loss_22: 2.4019 - dense_1_loss_23: 2.3446 - dense_1_loss_24: 2.2117 - dense_1_loss_25: 2.3597 - dense_1_loss_26: 2.3096 - dense_1_loss_27: 2.3818 - dense_1_loss_28: 2.4148 - dense_1_loss_29: 2.3202 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3167 - dense_1_acc_3: 0.3000 - dense_1_acc_4: 0.2167 - dense_1_acc_5: 0.3333 - dense_1_acc_6: 0.2667 - dense_1_acc_7: 0.3167 - dense_1_acc_8: 0.4000 - dense_1_acc_9: 0.2500 - dense_1_acc_10: 0.3833 - dense_1_acc_11: 0.3667 - dense_1_acc_12: 0.2000 - dense_1_acc_13: 0.3667 - dense_1_acc_14: 0.2667 - dense_1_acc_15: 0.3833 - dense_1_acc_16: 0.2500 - dense_1_acc_17: 0.4333 - dense_1_acc_18: 0.2833 - dense_1_acc_19: 0.2667 - dense_1_acc_20: 0.3000 - dense_1_acc_21: 0.3000 - dense_1_acc_22: 0.2000 - dense_1_acc_23: 0.3000 - dense_1_acc_24: 0.3000 - dense_1_acc_25: 0.2167 - dense_1_acc_26: 0.2500 - dense_1_acc_27: 0.3167 - dense_1_acc_28: 0.2167 - dense_1_acc_29: 0.3333 - dense_1_acc_30: 0.0000e+00     
Epoch 15/100
60/60 [==============================] - 0s - loss: 71.0470 - dense_1_loss_1: 4.1638 - dense_1_loss_2: 3.7607 - dense_1_loss_3: 3.3154 - dense_1_loss_4: 3.1078 - dense_1_loss_5: 2.7532 - dense_1_loss_6: 2.6089 - dense_1_loss_7: 2.5792 - dense_1_loss_8: 2.3008 - dense_1_loss_9: 2.4123 - dense_1_loss_10: 2.2561 - dense_1_loss_11: 2.4019 - dense_1_loss_12: 2.3221 - dense_1_loss_13: 2.0524 - dense_1_loss_14: 2.0567 - dense_1_loss_15: 2.1876 - dense_1_loss_16: 2.3408 - dense_1_loss_17: 2.1188 - dense_1_loss_18: 2.2255 - dense_1_loss_19: 2.1506 - dense_1_loss_20: 2.2751 - dense_1_loss_21: 2.1182 - dense_1_loss_22: 2.2486 - dense_1_loss_23: 2.2232 - dense_1_loss_24: 2.1508 - dense_1_loss_25: 2.1716 - dense_1_loss_26: 2.0658 - dense_1_loss_27: 2.2008 - dense_1_loss_28: 2.2633 - dense_1_loss_29: 2.2152 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3333 - dense_1_acc_3: 0.3167 - dense_1_acc_4: 0.2500 - dense_1_acc_5: 0.3333 - dense_1_acc_6: 0.3000 - dense_1_acc_7: 0.3333 - dense_1_acc_8: 0.3500 - dense_1_acc_9: 0.3000 - dense_1_acc_10: 0.3667 - dense_1_acc_11: 0.3667 - dense_1_acc_12: 0.3167 - dense_1_acc_13: 0.4333 - dense_1_acc_14: 0.3667 - dense_1_acc_15: 0.3667 - dense_1_acc_16: 0.2667 - dense_1_acc_17: 0.4667 - dense_1_acc_18: 0.3333 - dense_1_acc_19: 0.3667 - dense_1_acc_20: 0.3500 - dense_1_acc_21: 0.4500 - dense_1_acc_22: 0.3333 - dense_1_acc_23: 0.3333 - dense_1_acc_24: 0.4000 - dense_1_acc_25: 0.2667 - dense_1_acc_26: 0.4500 - dense_1_acc_27: 0.4500 - dense_1_acc_28: 0.3167 - dense_1_acc_29: 0.3667 - dense_1_acc_30: 0.0000e+00     
Epoch 16/100

60/60 [==============================] - 0s - loss: 67.1453 - dense_1_loss_1: 4.1549 - dense_1_loss_2: 3.7174 - dense_1_loss_3: 3.2314 - dense_1_loss_4: 2.9814 - dense_1_loss_5: 2.6265 - dense_1_loss_6: 2.4502 - dense_1_loss_7: 2.4540 - dense_1_loss_8: 2.1929 - dense_1_loss_9: 2.1878 - dense_1_loss_10: 2.1074 - dense_1_loss_11: 2.2140 - dense_1_loss_12: 2.1484 - dense_1_loss_13: 1.8475 - dense_1_loss_14: 1.9436 - dense_1_loss_15: 2.0624 - dense_1_loss_16: 2.2186 - dense_1_loss_17: 1.9101 - dense_1_loss_18: 2.0757 - dense_1_loss_19: 2.0032 - dense_1_loss_20: 2.0723 - dense_1_loss_21: 2.0182 - dense_1_loss_22: 2.1454 - dense_1_loss_23: 2.1055 - dense_1_loss_24: 2.0867 - dense_1_loss_25: 2.0845 - dense_1_loss_26: 1.9196 - dense_1_loss_27: 2.1060 - dense_1_loss_28: 2.0956 - dense_1_loss_29: 1.9841 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3333 - dense_1_acc_3: 0.3500 - dense_1_acc_4: 0.2833 - dense_1_acc_5: 0.4000 - dense_1_acc_6: 0.3333 - dense_1_acc_7: 0.3333 - dense_1_acc_8: 0.4167 - dense_1_acc_9: 0.3667 - dense_1_acc_10: 0.3833 - dense_1_acc_11: 0.4500 - dense_1_acc_12: 0.3833 - dense_1_acc_13: 0.5167 - dense_1_acc_14: 0.4167 - dense_1_acc_15: 0.4833 - dense_1_acc_16: 0.2667 - dense_1_acc_17: 0.4833 - dense_1_acc_18: 0.3833 - dense_1_acc_19: 0.3667 - dense_1_acc_20: 0.4000 - dense_1_acc_21: 0.4167 - dense_1_acc_22: 0.2833 - dense_1_acc_23: 0.3667 - dense_1_acc_24: 0.3000 - dense_1_acc_25: 0.2833 - dense_1_acc_26: 0.5333 - dense_1_acc_27: 0.3833 - dense_1_acc_28: 0.3667 - dense_1_acc_29: 0.4000 - dense_1_acc_30: 0.0000e+00     
Epoch 17/100
60/60 [==============================] - 0s - loss: 63.4511 - dense_1_loss_1: 4.1471 - dense_1_loss_2: 3.6721 - dense_1_loss_3: 3.1474 - dense_1_loss_4: 2.8561 - dense_1_loss_5: 2.5042 - dense_1_loss_6: 2.3212 - dense_1_loss_7: 2.3296 - dense_1_loss_8: 2.0707 - dense_1_loss_9: 2.0627 - dense_1_loss_10: 2.0097 - dense_1_loss_11: 2.0718 - dense_1_loss_12: 2.0302 - dense_1_loss_13: 1.7284 - dense_1_loss_14: 1.7868 - dense_1_loss_15: 1.9461 - dense_1_loss_16: 2.0716 - dense_1_loss_17: 1.8135 - dense_1_loss_18: 1.9484 - dense_1_loss_19: 1.8524 - dense_1_loss_20: 1.9478 - dense_1_loss_21: 1.8736 - dense_1_loss_22: 1.9967 - dense_1_loss_23: 1.9183 - dense_1_loss_24: 1.9553 - dense_1_loss_25: 1.9402 - dense_1_loss_26: 1.7694 - dense_1_loss_27: 1.9257 - dense_1_loss_28: 1.8849 - dense_1_loss_29: 1.8691 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3167 - dense_1_acc_3: 0.3500 - dense_1_acc_4: 0.3000 - dense_1_acc_5: 0.4000 - dense_1_acc_6: 0.4000 - dense_1_acc_7: 0.3667 - dense_1_acc_8: 0.5167 - dense_1_acc_9: 0.4167 - dense_1_acc_10: 0.4000 - dense_1_acc_11: 0.3833 - dense_1_acc_12: 0.4000 - dense_1_acc_13: 0.5500 - dense_1_acc_14: 0.4667 - dense_1_acc_15: 0.4000 - dense_1_acc_16: 0.3667 - dense_1_acc_17: 0.5167 - dense_1_acc_18: 0.3833 - dense_1_acc_19: 0.4667 - dense_1_acc_20: 0.4167 - dense_1_acc_21: 0.4667 - dense_1_acc_22: 0.3167 - dense_1_acc_23: 0.3833 - dense_1_acc_24: 0.4000 - dense_1_acc_25: 0.3667 - dense_1_acc_26: 0.4667 - dense_1_acc_27: 0.4000 - dense_1_acc_28: 0.3667 - dense_1_acc_29: 0.4500 - dense_1_acc_30: 0.0000e+00     
Epoch 18/100
60/60 [==============================] - 0s - loss: 59.8693 - dense_1_loss_1: 4.1373 - dense_1_loss_2: 3.6265 - dense_1_loss_3: 3.0677 - dense_1_loss_4: 2.7356 - dense_1_loss_5: 2.3790 - dense_1_loss_6: 2.1946 - dense_1_loss_7: 2.1806 - dense_1_loss_8: 1.9625 - dense_1_loss_9: 1.9246 - dense_1_loss_10: 1.8478 - dense_1_loss_11: 1.9315 - dense_1_loss_12: 1.8604 - dense_1_loss_13: 1.6713 - dense_1_loss_14: 1.7083 - dense_1_loss_15: 1.8166 - dense_1_loss_16: 1.9549 - dense_1_loss_17: 1.6620 - dense_1_loss_18: 1.7956 - dense_1_loss_19: 1.7486 - dense_1_loss_20: 1.8150 - dense_1_loss_21: 1.7090 - dense_1_loss_22: 1.8647 - dense_1_loss_23: 1.7891 - dense_1_loss_24: 1.7571 - dense_1_loss_25: 1.7971 - dense_1_loss_26: 1.6557 - dense_1_loss_27: 1.8108 - dense_1_loss_28: 1.7908 - dense_1_loss_29: 1.6747 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3167 - dense_1_acc_3: 0.3333 - dense_1_acc_4: 0.3000 - dense_1_acc_5: 0.4167 - dense_1_acc_6: 0.4000 - dense_1_acc_7: 0.4000 - dense_1_acc_8: 0.5000 - dense_1_acc_9: 0.4833 - dense_1_acc_10: 0.4833 - dense_1_acc_11: 0.4333 - dense_1_acc_12: 0.4167 - dense_1_acc_13: 0.5500 - dense_1_acc_14: 0.5333 - dense_1_acc_15: 0.5500 - dense_1_acc_16: 0.3833 - dense_1_acc_17: 0.5333 - dense_1_acc_18: 0.4667 - dense_1_acc_19: 0.5500 - dense_1_acc_20: 0.5000 - dense_1_acc_21: 0.5500 - dense_1_acc_22: 0.3833 - dense_1_acc_23: 0.4833 - dense_1_acc_24: 0.5167 - dense_1_acc_25: 0.3500 - dense_1_acc_26: 0.5333 - dense_1_acc_27: 0.4500 - dense_1_acc_28: 0.4000 - dense_1_acc_29: 0.5333 - dense_1_acc_30: 0.0000e+00     
Epoch 19/100
60/60 [==============================] - 0s - loss: 56.8391 - dense_1_loss_1: 4.1274 - dense_1_loss_2: 3.5817 - dense_1_loss_3: 2.9800 - dense_1_loss_4: 2.6088 - dense_1_loss_5: 2.2547 - dense_1_loss_6: 2.0663 - dense_1_loss_7: 2.0360 - dense_1_loss_8: 1.8352 - dense_1_loss_9: 1.7870 - dense_1_loss_10: 1.7139 - dense_1_loss_11: 1.8155 - dense_1_loss_12: 1.7159 - dense_1_loss_13: 1.5772 - dense_1_loss_14: 1.5844 - dense_1_loss_15: 1.6770 - dense_1_loss_16: 1.8365 - dense_1_loss_17: 1.5644 - dense_1_loss_18: 1.6584 - dense_1_loss_19: 1.6481 - dense_1_loss_20: 1.7579 - dense_1_loss_21: 1.6190 - dense_1_loss_22: 1.7324 - dense_1_loss_23: 1.6889 - dense_1_loss_24: 1.6760 - dense_1_loss_25: 1.7148 - dense_1_loss_26: 1.5838 - dense_1_loss_27: 1.7028 - dense_1_loss_28: 1.6689 - dense_1_loss_29: 1.6262 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3167 - dense_1_acc_3: 0.3333 - dense_1_acc_4: 0.3000 - dense_1_acc_5: 0.4167 - dense_1_acc_6: 0.4000 - dense_1_acc_7: 0.4000 - dense_1_acc_8: 0.5500 - dense_1_acc_9: 0.5833 - dense_1_acc_10: 0.5333 - dense_1_acc_11: 0.5000 - dense_1_acc_12: 0.5333 - dense_1_acc_13: 0.5667 - dense_1_acc_14: 0.6000 - dense_1_acc_15: 0.5667 - dense_1_acc_16: 0.4333 - dense_1_acc_17: 0.5333 - dense_1_acc_18: 0.5000 - dense_1_acc_19: 0.5667 - dense_1_acc_20: 0.4833 - dense_1_acc_21: 0.5500 - dense_1_acc_22: 0.4000 - dense_1_acc_23: 0.4833 - dense_1_acc_24: 0.5000 - dense_1_acc_25: 0.3500 - dense_1_acc_26: 0.4667 - dense_1_acc_27: 0.5000 - dense_1_acc_28: 0.5167 - dense_1_acc_29: 0.5167 - dense_1_acc_30: 0.0000e+00     
Epoch 20/100
60/60 [==============================] - 0s - loss: 53.9608 - dense_1_loss_1: 4.1174 - dense_1_loss_2: 3.5366 - dense_1_loss_3: 2.8881 - dense_1_loss_4: 2.4918 - dense_1_loss_5: 2.1515 - dense_1_loss_6: 1.9431 - dense_1_loss_7: 1.9163 - dense_1_loss_8: 1.7717 - dense_1_loss_9: 1.6791 - dense_1_loss_10: 1.6139 - dense_1_loss_11: 1.6933 - dense_1_loss_12: 1.6473 - dense_1_loss_13: 1.4890 - dense_1_loss_14: 1.5421 - dense_1_loss_15: 1.6128 - dense_1_loss_16: 1.7170 - dense_1_loss_17: 1.5189 - dense_1_loss_18: 1.5324 - dense_1_loss_19: 1.5721 - dense_1_loss_20: 1.6496 - dense_1_loss_21: 1.5518 - dense_1_loss_22: 1.6085 - dense_1_loss_23: 1.5435 - dense_1_loss_24: 1.5469 - dense_1_loss_25: 1.6517 - dense_1_loss_26: 1.4673 - dense_1_loss_27: 1.5057 - dense_1_loss_28: 1.5156 - dense_1_loss_29: 1.4857 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.2667 - dense_1_acc_3: 0.3500 - dense_1_acc_4: 0.3167 - dense_1_acc_5: 0.4167 - dense_1_acc_6: 0.4167 - dense_1_acc_7: 0.5000 - dense_1_acc_8: 0.5167 - dense_1_acc_9: 0.6000 - dense_1_acc_10: 0.5333 - dense_1_acc_11: 0.5667 - dense_1_acc_12: 0.5500 - dense_1_acc_13: 0.5833 - dense_1_acc_14: 0.6167 - dense_1_acc_15: 0.5833 - dense_1_acc_16: 0.5500 - dense_1_acc_17: 0.6000 - dense_1_acc_18: 0.5833 - dense_1_acc_19: 0.5333 - dense_1_acc_20: 0.4667 - dense_1_acc_21: 0.5333 - dense_1_acc_22: 0.4667 - dense_1_acc_23: 0.5667 - dense_1_acc_24: 0.5167 - dense_1_acc_25: 0.3667 - dense_1_acc_26: 0.6333 - dense_1_acc_27: 0.5500 - dense_1_acc_28: 0.5667 - dense_1_acc_29: 0.6667 - dense_1_acc_30: 0.0000e+00     
Epoch 21/100

60/60 [==============================] - 0s - loss: 50.9724 - dense_1_loss_1: 4.1076 - dense_1_loss_2: 3.4929 - dense_1_loss_3: 2.7980 - dense_1_loss_4: 2.3859 - dense_1_loss_5: 2.0493 - dense_1_loss_6: 1.8228 - dense_1_loss_7: 1.7876 - dense_1_loss_8: 1.6425 - dense_1_loss_9: 1.5580 - dense_1_loss_10: 1.4983 - dense_1_loss_11: 1.5669 - dense_1_loss_12: 1.5114 - dense_1_loss_13: 1.3566 - dense_1_loss_14: 1.3826 - dense_1_loss_15: 1.4836 - dense_1_loss_16: 1.5596 - dense_1_loss_17: 1.4056 - dense_1_loss_18: 1.4341 - dense_1_loss_19: 1.3891 - dense_1_loss_20: 1.4988 - dense_1_loss_21: 1.4914 - dense_1_loss_22: 1.5458 - dense_1_loss_23: 1.4681 - dense_1_loss_24: 1.4985 - dense_1_loss_25: 1.4873 - dense_1_loss_26: 1.4021 - dense_1_loss_27: 1.4572 - dense_1_loss_28: 1.4477 - dense_1_loss_29: 1.4428 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.2667 - dense_1_acc_3: 0.3667 - dense_1_acc_4: 0.3000 - dense_1_acc_5: 0.4167 - dense_1_acc_6: 0.4833 - dense_1_acc_7: 0.5000 - dense_1_acc_8: 0.6000 - dense_1_acc_9: 0.7167 - dense_1_acc_10: 0.5667 - dense_1_acc_11: 0.5833 - dense_1_acc_12: 0.5667 - dense_1_acc_13: 0.6667 - dense_1_acc_14: 0.6833 - dense_1_acc_15: 0.6333 - dense_1_acc_16: 0.5500 - dense_1_acc_17: 0.6000 - dense_1_acc_18: 0.6000 - dense_1_acc_19: 0.6333 - dense_1_acc_20: 0.5500 - dense_1_acc_21: 0.6167 - dense_1_acc_22: 0.4833 - dense_1_acc_23: 0.5833 - dense_1_acc_24: 0.5667 - dense_1_acc_25: 0.4167 - dense_1_acc_26: 0.6333 - dense_1_acc_27: 0.5833 - dense_1_acc_28: 0.6333 - dense_1_acc_29: 0.6500 - dense_1_acc_30: 0.0000e+00     
Epoch 22/100
60/60 [==============================] - 0s - loss: 48.1419 - dense_1_loss_1: 4.0996 - dense_1_loss_2: 3.4462 - dense_1_loss_3: 2.7139 - dense_1_loss_4: 2.2812 - dense_1_loss_5: 1.9578 - dense_1_loss_6: 1.7030 - dense_1_loss_7: 1.6686 - dense_1_loss_8: 1.5597 - dense_1_loss_9: 1.4766 - dense_1_loss_10: 1.4282 - dense_1_loss_11: 1.4587 - dense_1_loss_12: 1.4161 - dense_1_loss_13: 1.2799 - dense_1_loss_14: 1.3291 - dense_1_loss_15: 1.3986 - dense_1_loss_16: 1.4631 - dense_1_loss_17: 1.3300 - dense_1_loss_18: 1.3571 - dense_1_loss_19: 1.2914 - dense_1_loss_20: 1.3351 - dense_1_loss_21: 1.3880 - dense_1_loss_22: 1.4452 - dense_1_loss_23: 1.3411 - dense_1_loss_24: 1.3776 - dense_1_loss_25: 1.3264 - dense_1_loss_26: 1.3171 - dense_1_loss_27: 1.3541 - dense_1_loss_28: 1.3017 - dense_1_loss_29: 1.2969 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.2667 - dense_1_acc_3: 0.4000 - dense_1_acc_4: 0.3667 - dense_1_acc_5: 0.4500 - dense_1_acc_6: 0.4833 - dense_1_acc_7: 0.6000 - dense_1_acc_8: 0.6333 - dense_1_acc_9: 0.7333 - dense_1_acc_10: 0.6000 - dense_1_acc_11: 0.6500 - dense_1_acc_12: 0.6333 - dense_1_acc_13: 0.7500 - dense_1_acc_14: 0.7333 - dense_1_acc_15: 0.6167 - dense_1_acc_16: 0.6333 - dense_1_acc_17: 0.6667 - dense_1_acc_18: 0.7167 - dense_1_acc_19: 0.7500 - dense_1_acc_20: 0.7000 - dense_1_acc_21: 0.7000 - dense_1_acc_22: 0.6167 - dense_1_acc_23: 0.6833 - dense_1_acc_24: 0.6500 - dense_1_acc_25: 0.7000 - dense_1_acc_26: 0.7167 - dense_1_acc_27: 0.7000 - dense_1_acc_28: 0.7500 - dense_1_acc_29: 0.8167 - dense_1_acc_30: 0.0000e+00     
Epoch 23/100
60/60 [==============================] - 0s - loss: 45.7287 - dense_1_loss_1: 4.0906 - dense_1_loss_2: 3.3972 - dense_1_loss_3: 2.6275 - dense_1_loss_4: 2.1777 - dense_1_loss_5: 1.8672 - dense_1_loss_6: 1.6060 - dense_1_loss_7: 1.5667 - dense_1_loss_8: 1.4920 - dense_1_loss_9: 1.3864 - dense_1_loss_10: 1.3490 - dense_1_loss_11: 1.3747 - dense_1_loss_12: 1.3320 - dense_1_loss_13: 1.2020 - dense_1_loss_14: 1.2548 - dense_1_loss_15: 1.3103 - dense_1_loss_16: 1.3899 - dense_1_loss_17: 1.2478 - dense_1_loss_18: 1.2535 - dense_1_loss_19: 1.2335 - dense_1_loss_20: 1.2316 - dense_1_loss_21: 1.2768 - dense_1_loss_22: 1.3516 - dense_1_loss_23: 1.2325 - dense_1_loss_24: 1.2871 - dense_1_loss_25: 1.2500 - dense_1_loss_26: 1.2073 - dense_1_loss_27: 1.2727 - dense_1_loss_28: 1.2277 - dense_1_loss_29: 1.2328 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3167 - dense_1_acc_3: 0.4167 - dense_1_acc_4: 0.4167 - dense_1_acc_5: 0.4500 - dense_1_acc_6: 0.4667 - dense_1_acc_7: 0.7000 - dense_1_acc_8: 0.6667 - dense_1_acc_9: 0.7500 - dense_1_acc_10: 0.6333 - dense_1_acc_11: 0.7333 - dense_1_acc_12: 0.7167 - dense_1_acc_13: 0.8167 - dense_1_acc_14: 0.7667 - dense_1_acc_15: 0.6500 - dense_1_acc_16: 0.6500 - dense_1_acc_17: 0.7167 - dense_1_acc_18: 0.8000 - dense_1_acc_19: 0.7500 - dense_1_acc_20: 0.7667 - dense_1_acc_21: 0.7833 - dense_1_acc_22: 0.6000 - dense_1_acc_23: 0.8000 - dense_1_acc_24: 0.7000 - dense_1_acc_25: 0.7333 - dense_1_acc_26: 0.7667 - dense_1_acc_27: 0.7167 - dense_1_acc_28: 0.8000 - dense_1_acc_29: 0.8333 - dense_1_acc_30: 0.0000e+00     
Epoch 24/100
60/60 [==============================] - 0s - loss: 43.2462 - dense_1_loss_1: 4.0825 - dense_1_loss_2: 3.3486 - dense_1_loss_3: 2.5386 - dense_1_loss_4: 2.0778 - dense_1_loss_5: 1.7750 - dense_1_loss_6: 1.5065 - dense_1_loss_7: 1.4671 - dense_1_loss_8: 1.3835 - dense_1_loss_9: 1.2746 - dense_1_loss_10: 1.2554 - dense_1_loss_11: 1.2799 - dense_1_loss_12: 1.2090 - dense_1_loss_13: 1.0891 - dense_1_loss_14: 1.1303 - dense_1_loss_15: 1.2122 - dense_1_loss_16: 1.2736 - dense_1_loss_17: 1.1689 - dense_1_loss_18: 1.1656 - dense_1_loss_19: 1.1194 - dense_1_loss_20: 1.1911 - dense_1_loss_21: 1.1881 - dense_1_loss_22: 1.2469 - dense_1_loss_23: 1.1685 - dense_1_loss_24: 1.2128 - dense_1_loss_25: 1.2012 - dense_1_loss_26: 1.1428 - dense_1_loss_27: 1.1780 - dense_1_loss_28: 1.1789 - dense_1_loss_29: 1.1801 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3333 - dense_1_acc_3: 0.4333 - dense_1_acc_4: 0.4500 - dense_1_acc_5: 0.4500 - dense_1_acc_6: 0.5667 - dense_1_acc_7: 0.6667 - dense_1_acc_8: 0.6167 - dense_1_acc_9: 0.7667 - dense_1_acc_10: 0.6667 - dense_1_acc_11: 0.7333 - dense_1_acc_12: 0.7500 - dense_1_acc_13: 0.8833 - dense_1_acc_14: 0.8333 - dense_1_acc_15: 0.7667 - dense_1_acc_16: 0.6833 - dense_1_acc_17: 0.7667 - dense_1_acc_18: 0.8167 - dense_1_acc_19: 0.8667 - dense_1_acc_20: 0.7500 - dense_1_acc_21: 0.7333 - dense_1_acc_22: 0.6667 - dense_1_acc_23: 0.8000 - dense_1_acc_24: 0.6833 - dense_1_acc_25: 0.7167 - dense_1_acc_26: 0.7833 - dense_1_acc_27: 0.7667 - dense_1_acc_28: 0.7167 - dense_1_acc_29: 0.7667 - dense_1_acc_30: 0.0000e+00     
Epoch 25/100
60/60 [==============================] - 0s - loss: 41.0381 - dense_1_loss_1: 4.0739 - dense_1_loss_2: 3.2957 - dense_1_loss_3: 2.4566 - dense_1_loss_4: 1.9918 - dense_1_loss_5: 1.6961 - dense_1_loss_6: 1.4204 - dense_1_loss_7: 1.3666 - dense_1_loss_8: 1.3103 - dense_1_loss_9: 1.1911 - dense_1_loss_10: 1.1415 - dense_1_loss_11: 1.1687 - dense_1_loss_12: 1.1151 - dense_1_loss_13: 1.0507 - dense_1_loss_14: 1.0454 - dense_1_loss_15: 1.1417 - dense_1_loss_16: 1.1702 - dense_1_loss_17: 1.1268 - dense_1_loss_18: 1.1042 - dense_1_loss_19: 1.0411 - dense_1_loss_20: 1.1473 - dense_1_loss_21: 1.1245 - dense_1_loss_22: 1.1546 - dense_1_loss_23: 1.1001 - dense_1_loss_24: 1.0888 - dense_1_loss_25: 1.1753 - dense_1_loss_26: 1.0554 - dense_1_loss_27: 1.1186 - dense_1_loss_28: 1.0918 - dense_1_loss_29: 1.0739 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3333 - dense_1_acc_3: 0.4333 - dense_1_acc_4: 0.4500 - dense_1_acc_5: 0.4500 - dense_1_acc_6: 0.6000 - dense_1_acc_7: 0.7167 - dense_1_acc_8: 0.6500 - dense_1_acc_9: 0.8333 - dense_1_acc_10: 0.7167 - dense_1_acc_11: 0.7833 - dense_1_acc_12: 0.7667 - dense_1_acc_13: 0.9167 - dense_1_acc_14: 0.8667 - dense_1_acc_15: 0.7500 - dense_1_acc_16: 0.7833 - dense_1_acc_17: 0.8167 - dense_1_acc_18: 0.8000 - dense_1_acc_19: 0.8167 - dense_1_acc_20: 0.7667 - dense_1_acc_21: 0.7667 - dense_1_acc_22: 0.7333 - dense_1_acc_23: 0.8167 - dense_1_acc_24: 0.7333 - dense_1_acc_25: 0.6667 - dense_1_acc_26: 0.7667 - dense_1_acc_27: 0.7833 - dense_1_acc_28: 0.7667 - dense_1_acc_29: 0.7667 - dense_1_acc_30: 0.0000e+00         
Epoch 26/100

60/60 [==============================] - 0s - loss: 38.7576 - dense_1_loss_1: 4.0663 - dense_1_loss_2: 3.2406 - dense_1_loss_3: 2.3696 - dense_1_loss_4: 1.9020 - dense_1_loss_5: 1.6057 - dense_1_loss_6: 1.3208 - dense_1_loss_7: 1.2548 - dense_1_loss_8: 1.2333 - dense_1_loss_9: 1.1206 - dense_1_loss_10: 1.0850 - dense_1_loss_11: 1.0887 - dense_1_loss_12: 1.0589 - dense_1_loss_13: 0.9552 - dense_1_loss_14: 0.9603 - dense_1_loss_15: 1.0697 - dense_1_loss_16: 1.0753 - dense_1_loss_17: 1.0316 - dense_1_loss_18: 1.0102 - dense_1_loss_19: 0.9842 - dense_1_loss_20: 1.0580 - dense_1_loss_21: 1.0375 - dense_1_loss_22: 1.0719 - dense_1_loss_23: 1.0310 - dense_1_loss_24: 1.0371 - dense_1_loss_25: 1.0396 - dense_1_loss_26: 1.0294 - dense_1_loss_27: 1.0104 - dense_1_loss_28: 1.0096 - dense_1_loss_29: 1.0000 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3333 - dense_1_acc_3: 0.4333 - dense_1_acc_4: 0.4667 - dense_1_acc_5: 0.5500 - dense_1_acc_6: 0.7167 - dense_1_acc_7: 0.7833 - dense_1_acc_8: 0.7833 - dense_1_acc_9: 0.8833 - dense_1_acc_10: 0.8333 - dense_1_acc_11: 0.8667 - dense_1_acc_12: 0.7833 - dense_1_acc_13: 0.9333 - dense_1_acc_14: 0.9667 - dense_1_acc_15: 0.8167 - dense_1_acc_16: 0.8333 - dense_1_acc_17: 0.8833 - dense_1_acc_18: 0.8500 - dense_1_acc_19: 0.9000 - dense_1_acc_20: 0.8833 - dense_1_acc_21: 0.8667 - dense_1_acc_22: 0.7667 - dense_1_acc_23: 0.8667 - dense_1_acc_24: 0.8000 - dense_1_acc_25: 0.8333 - dense_1_acc_26: 0.8000 - dense_1_acc_27: 0.8667 - dense_1_acc_28: 0.8667 - dense_1_acc_29: 0.8667 - dense_1_acc_30: 0.0000e+00     
Epoch 27/100
60/60 [==============================] - 0s - loss: 36.6328 - dense_1_loss_1: 4.0582 - dense_1_loss_2: 3.1896 - dense_1_loss_3: 2.2883 - dense_1_loss_4: 1.8205 - dense_1_loss_5: 1.5165 - dense_1_loss_6: 1.2067 - dense_1_loss_7: 1.1492 - dense_1_loss_8: 1.1323 - dense_1_loss_9: 1.0449 - dense_1_loss_10: 0.9920 - dense_1_loss_11: 1.0012 - dense_1_loss_12: 0.9643 - dense_1_loss_13: 0.8887 - dense_1_loss_14: 0.8815 - dense_1_loss_15: 0.9902 - dense_1_loss_16: 1.0244 - dense_1_loss_17: 0.9603 - dense_1_loss_18: 0.9297 - dense_1_loss_19: 0.9068 - dense_1_loss_20: 0.9851 - dense_1_loss_21: 0.9706 - dense_1_loss_22: 1.0063 - dense_1_loss_23: 0.9468 - dense_1_loss_24: 0.9860 - dense_1_loss_25: 0.9935 - dense_1_loss_26: 0.9500 - dense_1_loss_27: 0.9397 - dense_1_loss_28: 0.9391 - dense_1_loss_29: 0.9704 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3500 - dense_1_acc_3: 0.4667 - dense_1_acc_4: 0.5167 - dense_1_acc_5: 0.6167 - dense_1_acc_6: 0.8167 - dense_1_acc_7: 0.8333 - dense_1_acc_8: 0.8333 - dense_1_acc_9: 0.9000 - dense_1_acc_10: 0.8667 - dense_1_acc_11: 0.8833 - dense_1_acc_12: 0.8167 - dense_1_acc_13: 0.9167 - dense_1_acc_14: 0.9667 - dense_1_acc_15: 0.8333 - dense_1_acc_16: 0.8167 - dense_1_acc_17: 0.9167 - dense_1_acc_18: 0.9000 - dense_1_acc_19: 0.8833 - dense_1_acc_20: 0.9333 - dense_1_acc_21: 0.8667 - dense_1_acc_22: 0.8667 - dense_1_acc_23: 0.9000 - dense_1_acc_24: 0.8167 - dense_1_acc_25: 0.8833 - dense_1_acc_26: 0.9167 - dense_1_acc_27: 0.9333 - dense_1_acc_28: 0.9333 - dense_1_acc_29: 0.9000 - dense_1_acc_30: 0.0000e+00     
Epoch 28/100
60/60 [==============================] - 0s - loss: 34.6476 - dense_1_loss_1: 4.0491 - dense_1_loss_2: 3.1351 - dense_1_loss_3: 2.2056 - dense_1_loss_4: 1.7515 - dense_1_loss_5: 1.4396 - dense_1_loss_6: 1.1227 - dense_1_loss_7: 1.0746 - dense_1_loss_8: 1.0619 - dense_1_loss_9: 0.9708 - dense_1_loss_10: 0.9191 - dense_1_loss_11: 0.9084 - dense_1_loss_12: 0.9415 - dense_1_loss_13: 0.8392 - dense_1_loss_14: 0.8242 - dense_1_loss_15: 0.9202 - dense_1_loss_16: 0.9383 - dense_1_loss_17: 0.8775 - dense_1_loss_18: 0.8664 - dense_1_loss_19: 0.8619 - dense_1_loss_20: 0.9143 - dense_1_loss_21: 0.8741 - dense_1_loss_22: 0.9524 - dense_1_loss_23: 0.8623 - dense_1_loss_24: 0.8945 - dense_1_loss_25: 0.9151 - dense_1_loss_26: 0.8513 - dense_1_loss_27: 0.9003 - dense_1_loss_28: 0.8819 - dense_1_loss_29: 0.8939 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3500 - dense_1_acc_3: 0.4667 - dense_1_acc_4: 0.5333 - dense_1_acc_5: 0.6333 - dense_1_acc_6: 0.8333 - dense_1_acc_7: 0.8333 - dense_1_acc_8: 0.8500 - dense_1_acc_9: 0.9000 - dense_1_acc_10: 0.9000 - dense_1_acc_11: 0.8667 - dense_1_acc_12: 0.8167 - dense_1_acc_13: 0.9333 - dense_1_acc_14: 0.9667 - dense_1_acc_15: 0.8500 - dense_1_acc_16: 0.9333 - dense_1_acc_17: 0.9167 - dense_1_acc_18: 0.9000 - dense_1_acc_19: 0.9000 - dense_1_acc_20: 0.9500 - dense_1_acc_21: 0.9167 - dense_1_acc_22: 0.8667 - dense_1_acc_23: 0.9167 - dense_1_acc_24: 0.9000 - dense_1_acc_25: 0.9333 - dense_1_acc_26: 0.9000 - dense_1_acc_27: 0.9333 - dense_1_acc_28: 0.9500 - dense_1_acc_29: 0.9167 - dense_1_acc_30: 0.0000e+00     
Epoch 29/100
60/60 [==============================] - 0s - loss: 32.7373 - dense_1_loss_1: 4.0411 - dense_1_loss_2: 3.0843 - dense_1_loss_3: 2.1271 - dense_1_loss_4: 1.6768 - dense_1_loss_5: 1.3652 - dense_1_loss_6: 1.0474 - dense_1_loss_7: 1.0085 - dense_1_loss_8: 0.9848 - dense_1_loss_9: 0.9122 - dense_1_loss_10: 0.8354 - dense_1_loss_11: 0.8332 - dense_1_loss_12: 0.8655 - dense_1_loss_13: 0.7736 - dense_1_loss_14: 0.7555 - dense_1_loss_15: 0.8490 - dense_1_loss_16: 0.8565 - dense_1_loss_17: 0.8094 - dense_1_loss_18: 0.8012 - dense_1_loss_19: 0.7902 - dense_1_loss_20: 0.8756 - dense_1_loss_21: 0.8122 - dense_1_loss_22: 0.8685 - dense_1_loss_23: 0.8113 - dense_1_loss_24: 0.8329 - dense_1_loss_25: 0.8406 - dense_1_loss_26: 0.8013 - dense_1_loss_27: 0.8319 - dense_1_loss_28: 0.8194 - dense_1_loss_29: 0.8267 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3500 - dense_1_acc_3: 0.4833 - dense_1_acc_4: 0.5500 - dense_1_acc_5: 0.6667 - dense_1_acc_6: 0.8500 - dense_1_acc_7: 0.8333 - dense_1_acc_8: 0.9000 - dense_1_acc_9: 0.9500 - dense_1_acc_10: 0.9167 - dense_1_acc_11: 0.8667 - dense_1_acc_12: 0.9000 - dense_1_acc_13: 0.9500 - dense_1_acc_14: 0.9667 - dense_1_acc_15: 0.9167 - dense_1_acc_16: 0.9667 - dense_1_acc_17: 0.9000 - dense_1_acc_18: 0.9333 - dense_1_acc_19: 0.9500 - dense_1_acc_20: 0.9000 - dense_1_acc_21: 0.9167 - dense_1_acc_22: 0.8833 - dense_1_acc_23: 0.9333 - dense_1_acc_24: 0.9333 - dense_1_acc_25: 0.9000 - dense_1_acc_26: 0.9000 - dense_1_acc_27: 0.9833 - dense_1_acc_28: 0.9500 - dense_1_acc_29: 0.9167 - dense_1_acc_30: 0.0000e+00     
Epoch 30/100
60/60 [==============================] - 0s - loss: 30.9302 - dense_1_loss_1: 4.0334 - dense_1_loss_2: 3.0289 - dense_1_loss_3: 2.0513 - dense_1_loss_4: 1.5961 - dense_1_loss_5: 1.2889 - dense_1_loss_6: 0.9690 - dense_1_loss_7: 0.9386 - dense_1_loss_8: 0.9192 - dense_1_loss_9: 0.8346 - dense_1_loss_10: 0.7810 - dense_1_loss_11: 0.7632 - dense_1_loss_12: 0.7935 - dense_1_loss_13: 0.6792 - dense_1_loss_14: 0.6982 - dense_1_loss_15: 0.7752 - dense_1_loss_16: 0.7905 - dense_1_loss_17: 0.7406 - dense_1_loss_18: 0.7408 - dense_1_loss_19: 0.7229 - dense_1_loss_20: 0.8163 - dense_1_loss_21: 0.7803 - dense_1_loss_22: 0.8086 - dense_1_loss_23: 0.7526 - dense_1_loss_24: 0.7759 - dense_1_loss_25: 0.7642 - dense_1_loss_26: 0.7825 - dense_1_loss_27: 0.7656 - dense_1_loss_28: 0.7583 - dense_1_loss_29: 0.7808 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3500 - dense_1_acc_3: 0.5167 - dense_1_acc_4: 0.5833 - dense_1_acc_5: 0.7167 - dense_1_acc_6: 0.8667 - dense_1_acc_7: 0.8333 - dense_1_acc_8: 0.8667 - dense_1_acc_9: 0.9333 - dense_1_acc_10: 0.9667 - dense_1_acc_11: 0.9000 - dense_1_acc_12: 0.9333 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 0.9667 - dense_1_acc_15: 0.9333 - dense_1_acc_16: 0.9833 - dense_1_acc_17: 0.9667 - dense_1_acc_18: 0.9667 - dense_1_acc_19: 0.9833 - dense_1_acc_20: 0.9500 - dense_1_acc_21: 0.9167 - dense_1_acc_22: 0.9500 - dense_1_acc_23: 0.9333 - dense_1_acc_24: 0.9167 - dense_1_acc_25: 0.9167 - dense_1_acc_26: 0.9167 - dense_1_acc_27: 0.9667 - dense_1_acc_28: 0.9500 - dense_1_acc_29: 0.9500 - dense_1_acc_30: 0.0000e+00     
Epoch 31/100

60/60 [==============================] - 0s - loss: 29.2263 - dense_1_loss_1: 4.0257 - dense_1_loss_2: 2.9800 - dense_1_loss_3: 1.9785 - dense_1_loss_4: 1.5118 - dense_1_loss_5: 1.2178 - dense_1_loss_6: 0.8913 - dense_1_loss_7: 0.8727 - dense_1_loss_8: 0.8639 - dense_1_loss_9: 0.7860 - dense_1_loss_10: 0.7316 - dense_1_loss_11: 0.7062 - dense_1_loss_12: 0.7396 - dense_1_loss_13: 0.6447 - dense_1_loss_14: 0.6389 - dense_1_loss_15: 0.7213 - dense_1_loss_16: 0.7306 - dense_1_loss_17: 0.6884 - dense_1_loss_18: 0.6833 - dense_1_loss_19: 0.6631 - dense_1_loss_20: 0.7434 - dense_1_loss_21: 0.7213 - dense_1_loss_22: 0.7481 - dense_1_loss_23: 0.6974 - dense_1_loss_24: 0.6974 - dense_1_loss_25: 0.7013 - dense_1_loss_26: 0.7224 - dense_1_loss_27: 0.6938 - dense_1_loss_28: 0.6959 - dense_1_loss_29: 0.7302 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3500 - dense_1_acc_3: 0.5333 - dense_1_acc_4: 0.6000 - dense_1_acc_5: 0.6833 - dense_1_acc_6: 0.8833 - dense_1_acc_7: 0.8500 - dense_1_acc_8: 0.9000 - dense_1_acc_9: 0.9500 - dense_1_acc_10: 0.9500 - dense_1_acc_11: 0.9500 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 0.9833 - dense_1_acc_14: 0.9833 - dense_1_acc_15: 0.9667 - dense_1_acc_16: 0.9500 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 0.9833 - dense_1_acc_19: 0.9833 - dense_1_acc_20: 0.9667 - dense_1_acc_21: 0.9333 - dense_1_acc_22: 0.9667 - dense_1_acc_23: 0.9333 - dense_1_acc_24: 0.9333 - dense_1_acc_25: 0.9500 - dense_1_acc_26: 0.9167 - dense_1_acc_27: 0.9833 - dense_1_acc_28: 0.9667 - dense_1_acc_29: 0.9500 - dense_1_acc_30: 0.0000e+00     
Epoch 32/100
60/60 [==============================] - 0s - loss: 27.5800 - dense_1_loss_1: 4.0183 - dense_1_loss_2: 2.9282 - dense_1_loss_3: 1.9086 - dense_1_loss_4: 1.4335 - dense_1_loss_5: 1.1433 - dense_1_loss_6: 0.8195 - dense_1_loss_7: 0.7994 - dense_1_loss_8: 0.8059 - dense_1_loss_9: 0.7225 - dense_1_loss_10: 0.6671 - dense_1_loss_11: 0.6424 - dense_1_loss_12: 0.6684 - dense_1_loss_13: 0.5962 - dense_1_loss_14: 0.5887 - dense_1_loss_15: 0.6747 - dense_1_loss_16: 0.6714 - dense_1_loss_17: 0.6320 - dense_1_loss_18: 0.6300 - dense_1_loss_19: 0.6059 - dense_1_loss_20: 0.6790 - dense_1_loss_21: 0.6738 - dense_1_loss_22: 0.6928 - dense_1_loss_23: 0.6517 - dense_1_loss_24: 0.6336 - dense_1_loss_25: 0.6427 - dense_1_loss_26: 0.6662 - dense_1_loss_27: 0.6604 - dense_1_loss_28: 0.6480 - dense_1_loss_29: 0.6759 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3667 - dense_1_acc_3: 0.5333 - dense_1_acc_4: 0.6000 - dense_1_acc_5: 0.7333 - dense_1_acc_6: 0.9000 - dense_1_acc_7: 0.8667 - dense_1_acc_8: 0.9000 - dense_1_acc_9: 0.9667 - dense_1_acc_10: 0.9667 - dense_1_acc_11: 0.9667 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 0.9833 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 0.9500 - dense_1_acc_16: 0.9500 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 0.9833 - dense_1_acc_21: 0.9667 - dense_1_acc_22: 0.9833 - dense_1_acc_23: 0.9667 - dense_1_acc_24: 0.9667 - dense_1_acc_25: 0.9667 - dense_1_acc_26: 0.9500 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 0.9833 - dense_1_acc_29: 0.9333 - dense_1_acc_30: 0.0000e+00     
Epoch 33/100
60/60 [==============================] - 0s - loss: 26.0498 - dense_1_loss_1: 4.0116 - dense_1_loss_2: 2.8754 - dense_1_loss_3: 1.8385 - dense_1_loss_4: 1.3620 - dense_1_loss_5: 1.0693 - dense_1_loss_6: 0.7710 - dense_1_loss_7: 0.7361 - dense_1_loss_8: 0.7417 - dense_1_loss_9: 0.6749 - dense_1_loss_10: 0.6071 - dense_1_loss_11: 0.5968 - dense_1_loss_12: 0.6103 - dense_1_loss_13: 0.5310 - dense_1_loss_14: 0.5402 - dense_1_loss_15: 0.6187 - dense_1_loss_16: 0.6118 - dense_1_loss_17: 0.5762 - dense_1_loss_18: 0.5807 - dense_1_loss_19: 0.5696 - dense_1_loss_20: 0.6311 - dense_1_loss_21: 0.6238 - dense_1_loss_22: 0.6368 - dense_1_loss_23: 0.6064 - dense_1_loss_24: 0.5945 - dense_1_loss_25: 0.5881 - dense_1_loss_26: 0.6177 - dense_1_loss_27: 0.6047 - dense_1_loss_28: 0.5994 - dense_1_loss_29: 0.6245 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3500 - dense_1_acc_3: 0.6000 - dense_1_acc_4: 0.6000 - dense_1_acc_5: 0.7667 - dense_1_acc_6: 0.9000 - dense_1_acc_7: 0.8667 - dense_1_acc_8: 0.9333 - dense_1_acc_9: 0.9667 - dense_1_acc_10: 0.9833 - dense_1_acc_11: 0.9667 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 0.9833 - dense_1_acc_16: 0.9667 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 0.9833 - dense_1_acc_21: 0.9833 - dense_1_acc_22: 0.9833 - dense_1_acc_23: 0.9667 - dense_1_acc_24: 0.9667 - dense_1_acc_25: 0.9833 - dense_1_acc_26: 0.9500 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9500 - dense_1_acc_30: 0.0000e+00     
Epoch 34/100
60/60 [==============================] - 0s - loss: 24.6717 - dense_1_loss_1: 4.0041 - dense_1_loss_2: 2.8275 - dense_1_loss_3: 1.7748 - dense_1_loss_4: 1.2846 - dense_1_loss_5: 0.9991 - dense_1_loss_6: 0.7148 - dense_1_loss_7: 0.6851 - dense_1_loss_8: 0.6910 - dense_1_loss_9: 0.6374 - dense_1_loss_10: 0.5712 - dense_1_loss_11: 0.5528 - dense_1_loss_12: 0.5734 - dense_1_loss_13: 0.4888 - dense_1_loss_14: 0.4973 - dense_1_loss_15: 0.5650 - dense_1_loss_16: 0.5737 - dense_1_loss_17: 0.5352 - dense_1_loss_18: 0.5338 - dense_1_loss_19: 0.5372 - dense_1_loss_20: 0.5928 - dense_1_loss_21: 0.5720 - dense_1_loss_22: 0.5792 - dense_1_loss_23: 0.5414 - dense_1_loss_24: 0.5514 - dense_1_loss_25: 0.5561 - dense_1_loss_26: 0.5752 - dense_1_loss_27: 0.5351 - dense_1_loss_28: 0.5437 - dense_1_loss_29: 0.5782 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3833 - dense_1_acc_3: 0.6000 - dense_1_acc_4: 0.6000 - dense_1_acc_5: 0.8167 - dense_1_acc_6: 0.9000 - dense_1_acc_7: 0.8833 - dense_1_acc_8: 0.9667 - dense_1_acc_9: 0.9667 - dense_1_acc_10: 0.9833 - dense_1_acc_11: 0.9667 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 0.9833 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 0.9833 - dense_1_acc_23: 0.9833 - dense_1_acc_24: 0.9833 - dense_1_acc_25: 0.9667 - dense_1_acc_26: 0.9500 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9333 - dense_1_acc_30: 0.0000e+00     
Epoch 35/100
60/60 [==============================] - 0s - loss: 23.2958 - dense_1_loss_1: 3.9975 - dense_1_loss_2: 2.7771 - dense_1_loss_3: 1.7097 - dense_1_loss_4: 1.2071 - dense_1_loss_5: 0.9388 - dense_1_loss_6: 0.6550 - dense_1_loss_7: 0.6300 - dense_1_loss_8: 0.6482 - dense_1_loss_9: 0.5862 - dense_1_loss_10: 0.5262 - dense_1_loss_11: 0.5018 - dense_1_loss_12: 0.5252 - dense_1_loss_13: 0.4495 - dense_1_loss_14: 0.4524 - dense_1_loss_15: 0.5257 - dense_1_loss_16: 0.5183 - dense_1_loss_17: 0.4920 - dense_1_loss_18: 0.4913 - dense_1_loss_19: 0.4929 - dense_1_loss_20: 0.5346 - dense_1_loss_21: 0.5224 - dense_1_loss_22: 0.5416 - dense_1_loss_23: 0.5028 - dense_1_loss_24: 0.4935 - dense_1_loss_25: 0.5007 - dense_1_loss_26: 0.5235 - dense_1_loss_27: 0.5069 - dense_1_loss_28: 0.5015 - dense_1_loss_29: 0.5433 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3833 - dense_1_acc_3: 0.6167 - dense_1_acc_4: 0.7000 - dense_1_acc_5: 0.8167 - dense_1_acc_6: 0.9167 - dense_1_acc_7: 0.9667 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9667 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 0.9833 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 0.9833 - dense_1_acc_26: 0.9500 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9667 - dense_1_acc_30: 0.0000e+00     
Epoch 36/100

60/60 [==============================] - 0s - loss: 22.0780 - dense_1_loss_1: 3.9919 - dense_1_loss_2: 2.7275 - dense_1_loss_3: 1.6486 - dense_1_loss_4: 1.1306 - dense_1_loss_5: 0.8770 - dense_1_loss_6: 0.5971 - dense_1_loss_7: 0.5839 - dense_1_loss_8: 0.6011 - dense_1_loss_9: 0.5364 - dense_1_loss_10: 0.4828 - dense_1_loss_11: 0.4530 - dense_1_loss_12: 0.4764 - dense_1_loss_13: 0.4087 - dense_1_loss_14: 0.4067 - dense_1_loss_15: 0.4904 - dense_1_loss_16: 0.4798 - dense_1_loss_17: 0.4598 - dense_1_loss_18: 0.4531 - dense_1_loss_19: 0.4442 - dense_1_loss_20: 0.4948 - dense_1_loss_21: 0.4927 - dense_1_loss_22: 0.5060 - dense_1_loss_23: 0.4753 - dense_1_loss_24: 0.4565 - dense_1_loss_25: 0.4578 - dense_1_loss_26: 0.4913 - dense_1_loss_27: 0.4725 - dense_1_loss_28: 0.4621 - dense_1_loss_29: 0.5202 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3833 - dense_1_acc_3: 0.6500 - dense_1_acc_4: 0.7333 - dense_1_acc_5: 0.8333 - dense_1_acc_6: 0.9500 - dense_1_acc_7: 0.9667 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 0.9833 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 0.9833 - dense_1_acc_26: 0.9500 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9500 - dense_1_acc_30: 0.0000e+00     
Epoch 37/100
60/60 [==============================] - 0s - loss: 20.8764 - dense_1_loss_1: 3.9852 - dense_1_loss_2: 2.6785 - dense_1_loss_3: 1.5887 - dense_1_loss_4: 1.0624 - dense_1_loss_5: 0.8189 - dense_1_loss_6: 0.5631 - dense_1_loss_7: 0.5438 - dense_1_loss_8: 0.5586 - dense_1_loss_9: 0.4994 - dense_1_loss_10: 0.4414 - dense_1_loss_11: 0.4202 - dense_1_loss_12: 0.4389 - dense_1_loss_13: 0.3698 - dense_1_loss_14: 0.3755 - dense_1_loss_15: 0.4432 - dense_1_loss_16: 0.4440 - dense_1_loss_17: 0.4244 - dense_1_loss_18: 0.4096 - dense_1_loss_19: 0.4076 - dense_1_loss_20: 0.4607 - dense_1_loss_21: 0.4495 - dense_1_loss_22: 0.4598 - dense_1_loss_23: 0.4308 - dense_1_loss_24: 0.4251 - dense_1_loss_25: 0.4169 - dense_1_loss_26: 0.4543 - dense_1_loss_27: 0.4127 - dense_1_loss_28: 0.4162 - dense_1_loss_29: 0.4770 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3833 - dense_1_acc_3: 0.6833 - dense_1_acc_4: 0.7500 - dense_1_acc_5: 0.8833 - dense_1_acc_6: 0.9500 - dense_1_acc_7: 0.9667 - dense_1_acc_8: 0.9500 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 0.9833 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 0.9833 - dense_1_acc_26: 0.9500 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9667 - dense_1_acc_30: 0.0000e+00     
Epoch 38/100
60/60 [==============================] - 0s - loss: 19.8255 - dense_1_loss_1: 3.9792 - dense_1_loss_2: 2.6316 - dense_1_loss_3: 1.5336 - dense_1_loss_4: 0.9940 - dense_1_loss_5: 0.7650 - dense_1_loss_6: 0.5319 - dense_1_loss_7: 0.5006 - dense_1_loss_8: 0.5288 - dense_1_loss_9: 0.4576 - dense_1_loss_10: 0.4081 - dense_1_loss_11: 0.3919 - dense_1_loss_12: 0.4033 - dense_1_loss_13: 0.3329 - dense_1_loss_14: 0.3614 - dense_1_loss_15: 0.3965 - dense_1_loss_16: 0.4153 - dense_1_loss_17: 0.3899 - dense_1_loss_18: 0.3756 - dense_1_loss_19: 0.3839 - dense_1_loss_20: 0.4274 - dense_1_loss_21: 0.4095 - dense_1_loss_22: 0.4244 - dense_1_loss_23: 0.3857 - dense_1_loss_24: 0.3950 - dense_1_loss_25: 0.3868 - dense_1_loss_26: 0.4135 - dense_1_loss_27: 0.3822 - dense_1_loss_28: 0.3871 - dense_1_loss_29: 0.4328 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3833 - dense_1_acc_3: 0.6833 - dense_1_acc_4: 0.7500 - dense_1_acc_5: 0.8833 - dense_1_acc_6: 0.9667 - dense_1_acc_7: 0.9667 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 0.9833 - dense_1_acc_26: 0.9500 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9667 - dense_1_acc_30: 0.0000e+00     
Epoch 39/100
60/60 [==============================] - 0s - loss: 18.7830 - dense_1_loss_1: 3.9737 - dense_1_loss_2: 2.5850 - dense_1_loss_3: 1.4763 - dense_1_loss_4: 0.9286 - dense_1_loss_5: 0.7128 - dense_1_loss_6: 0.4862 - dense_1_loss_7: 0.4679 - dense_1_loss_8: 0.4899 - dense_1_loss_9: 0.4209 - dense_1_loss_10: 0.3747 - dense_1_loss_11: 0.3503 - dense_1_loss_12: 0.3601 - dense_1_loss_13: 0.3045 - dense_1_loss_14: 0.3264 - dense_1_loss_15: 0.3647 - dense_1_loss_16: 0.3777 - dense_1_loss_17: 0.3586 - dense_1_loss_18: 0.3511 - dense_1_loss_19: 0.3449 - dense_1_loss_20: 0.4005 - dense_1_loss_21: 0.3754 - dense_1_loss_22: 0.3925 - dense_1_loss_23: 0.3549 - dense_1_loss_24: 0.3575 - dense_1_loss_25: 0.3624 - dense_1_loss_26: 0.3729 - dense_1_loss_27: 0.3535 - dense_1_loss_28: 0.3550 - dense_1_loss_29: 0.4040 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.3833 - dense_1_acc_3: 0.6833 - dense_1_acc_4: 0.7833 - dense_1_acc_5: 0.9167 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 0.9667 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 0.9833 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9667 - dense_1_acc_30: 0.0000e+00     
Epoch 40/100
60/60 [==============================] - 0s - loss: 17.8982 - dense_1_loss_1: 3.9677 - dense_1_loss_2: 2.5414 - dense_1_loss_3: 1.4264 - dense_1_loss_4: 0.8662 - dense_1_loss_5: 0.6650 - dense_1_loss_6: 0.4515 - dense_1_loss_7: 0.4321 - dense_1_loss_8: 0.4474 - dense_1_loss_9: 0.3942 - dense_1_loss_10: 0.3431 - dense_1_loss_11: 0.3201 - dense_1_loss_12: 0.3297 - dense_1_loss_13: 0.2829 - dense_1_loss_14: 0.2928 - dense_1_loss_15: 0.3352 - dense_1_loss_16: 0.3417 - dense_1_loss_17: 0.3265 - dense_1_loss_18: 0.3302 - dense_1_loss_19: 0.3248 - dense_1_loss_20: 0.3556 - dense_1_loss_21: 0.3565 - dense_1_loss_22: 0.3618 - dense_1_loss_23: 0.3377 - dense_1_loss_24: 0.3296 - dense_1_loss_25: 0.3282 - dense_1_loss_26: 0.3531 - dense_1_loss_27: 0.3271 - dense_1_loss_28: 0.3360 - dense_1_loss_29: 0.3937 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4000 - dense_1_acc_3: 0.6833 - dense_1_acc_4: 0.8333 - dense_1_acc_5: 0.9333 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 0.9667 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 0.9833 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9667 - dense_1_acc_30: 0.0000e+00     
Epoch 41/100

60/60 [==============================] - 0s - loss: 17.0105 - dense_1_loss_1: 3.9621 - dense_1_loss_2: 2.4965 - dense_1_loss_3: 1.3757 - dense_1_loss_4: 0.8071 - dense_1_loss_5: 0.6225 - dense_1_loss_6: 0.4251 - dense_1_loss_7: 0.4007 - dense_1_loss_8: 0.4155 - dense_1_loss_9: 0.3633 - dense_1_loss_10: 0.3153 - dense_1_loss_11: 0.2966 - dense_1_loss_12: 0.3041 - dense_1_loss_13: 0.2608 - dense_1_loss_14: 0.2748 - dense_1_loss_15: 0.3071 - dense_1_loss_16: 0.3171 - dense_1_loss_17: 0.2996 - dense_1_loss_18: 0.2996 - dense_1_loss_19: 0.3045 - dense_1_loss_20: 0.3246 - dense_1_loss_21: 0.3271 - dense_1_loss_22: 0.3314 - dense_1_loss_23: 0.3061 - dense_1_loss_24: 0.2982 - dense_1_loss_25: 0.2987 - dense_1_loss_26: 0.3226 - dense_1_loss_27: 0.2983 - dense_1_loss_28: 0.2979 - dense_1_loss_29: 0.3577 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4000 - dense_1_acc_3: 0.6833 - dense_1_acc_4: 0.8500 - dense_1_acc_5: 0.9667 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 0.9667 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 0.9833 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 0.9833 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9667 - dense_1_acc_30: 0.0000e+00     
Epoch 42/100
60/60 [==============================] - 0s - loss: 16.2433 - dense_1_loss_1: 3.9560 - dense_1_loss_2: 2.4548 - dense_1_loss_3: 1.3268 - dense_1_loss_4: 0.7513 - dense_1_loss_5: 0.5825 - dense_1_loss_6: 0.4006 - dense_1_loss_7: 0.3749 - dense_1_loss_8: 0.3886 - dense_1_loss_9: 0.3367 - dense_1_loss_10: 0.2905 - dense_1_loss_11: 0.2768 - dense_1_loss_12: 0.2798 - dense_1_loss_13: 0.2375 - dense_1_loss_14: 0.2571 - dense_1_loss_15: 0.2803 - dense_1_loss_16: 0.3001 - dense_1_loss_17: 0.2808 - dense_1_loss_18: 0.2725 - dense_1_loss_19: 0.2775 - dense_1_loss_20: 0.3112 - dense_1_loss_21: 0.2995 - dense_1_loss_22: 0.3061 - dense_1_loss_23: 0.2816 - dense_1_loss_24: 0.2780 - dense_1_loss_25: 0.2822 - dense_1_loss_26: 0.2890 - dense_1_loss_27: 0.2758 - dense_1_loss_28: 0.2756 - dense_1_loss_29: 0.3192 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4000 - dense_1_acc_3: 0.6833 - dense_1_acc_4: 0.8833 - dense_1_acc_5: 0.9667 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 0.9667 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00         
Epoch 43/100
60/60 [==============================] - 0s - loss: 15.5054 - dense_1_loss_1: 3.9511 - dense_1_loss_2: 2.4100 - dense_1_loss_3: 1.2817 - dense_1_loss_4: 0.6999 - dense_1_loss_5: 0.5438 - dense_1_loss_6: 0.3788 - dense_1_loss_7: 0.3445 - dense_1_loss_8: 0.3551 - dense_1_loss_9: 0.3104 - dense_1_loss_10: 0.2643 - dense_1_loss_11: 0.2592 - dense_1_loss_12: 0.2616 - dense_1_loss_13: 0.2144 - dense_1_loss_14: 0.2365 - dense_1_loss_15: 0.2588 - dense_1_loss_16: 0.2687 - dense_1_loss_17: 0.2531 - dense_1_loss_18: 0.2536 - dense_1_loss_19: 0.2616 - dense_1_loss_20: 0.2717 - dense_1_loss_21: 0.2748 - dense_1_loss_22: 0.2907 - dense_1_loss_23: 0.2612 - dense_1_loss_24: 0.2578 - dense_1_loss_25: 0.2484 - dense_1_loss_26: 0.2685 - dense_1_loss_27: 0.2575 - dense_1_loss_28: 0.2634 - dense_1_loss_29: 0.3044 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4000 - dense_1_acc_3: 0.7000 - dense_1_acc_4: 0.8833 - dense_1_acc_5: 0.9667 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 0.9833 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9667 - dense_1_acc_30: 0.0000e+00     
Epoch 44/100
60/60 [==============================] - 0s - loss: 14.8455 - dense_1_loss_1: 3.9456 - dense_1_loss_2: 2.3692 - dense_1_loss_3: 1.2391 - dense_1_loss_4: 0.6483 - dense_1_loss_5: 0.5138 - dense_1_loss_6: 0.3523 - dense_1_loss_7: 0.3198 - dense_1_loss_8: 0.3317 - dense_1_loss_9: 0.2878 - dense_1_loss_10: 0.2443 - dense_1_loss_11: 0.2374 - dense_1_loss_12: 0.2383 - dense_1_loss_13: 0.1957 - dense_1_loss_14: 0.2162 - dense_1_loss_15: 0.2402 - dense_1_loss_16: 0.2466 - dense_1_loss_17: 0.2364 - dense_1_loss_18: 0.2349 - dense_1_loss_19: 0.2390 - dense_1_loss_20: 0.2515 - dense_1_loss_21: 0.2562 - dense_1_loss_22: 0.2664 - dense_1_loss_23: 0.2445 - dense_1_loss_24: 0.2385 - dense_1_loss_25: 0.2324 - dense_1_loss_26: 0.2477 - dense_1_loss_27: 0.2419 - dense_1_loss_28: 0.2442 - dense_1_loss_29: 0.2855 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4167 - dense_1_acc_3: 0.7000 - dense_1_acc_4: 0.9333 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 0.9833 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9667 - dense_1_acc_30: 0.0000e+00     
Epoch 45/100
60/60 [==============================] - 0s - loss: 14.2385 - dense_1_loss_1: 3.9414 - dense_1_loss_2: 2.3279 - dense_1_loss_3: 1.1949 - dense_1_loss_4: 0.6057 - dense_1_loss_5: 0.4788 - dense_1_loss_6: 0.3265 - dense_1_loss_7: 0.2958 - dense_1_loss_8: 0.3100 - dense_1_loss_9: 0.2652 - dense_1_loss_10: 0.2307 - dense_1_loss_11: 0.2177 - dense_1_loss_12: 0.2152 - dense_1_loss_13: 0.1824 - dense_1_loss_14: 0.2014 - dense_1_loss_15: 0.2236 - dense_1_loss_16: 0.2413 - dense_1_loss_17: 0.2230 - dense_1_loss_18: 0.2143 - dense_1_loss_19: 0.2190 - dense_1_loss_20: 0.2532 - dense_1_loss_21: 0.2378 - dense_1_loss_22: 0.2414 - dense_1_loss_23: 0.2267 - dense_1_loss_24: 0.2125 - dense_1_loss_25: 0.2283 - dense_1_loss_26: 0.2256 - dense_1_loss_27: 0.2213 - dense_1_loss_28: 0.2211 - dense_1_loss_29: 0.2557 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4167 - dense_1_acc_3: 0.7167 - dense_1_acc_4: 0.9333 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 0.9833 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 46/100

60/60 [==============================] - 0s - loss: 13.6498 - dense_1_loss_1: 3.9356 - dense_1_loss_2: 2.2878 - dense_1_loss_3: 1.1598 - dense_1_loss_4: 0.5648 - dense_1_loss_5: 0.4495 - dense_1_loss_6: 0.3106 - dense_1_loss_7: 0.2724 - dense_1_loss_8: 0.2874 - dense_1_loss_9: 0.2458 - dense_1_loss_10: 0.2136 - dense_1_loss_11: 0.2047 - dense_1_loss_12: 0.2002 - dense_1_loss_13: 0.1702 - dense_1_loss_14: 0.1875 - dense_1_loss_15: 0.2023 - dense_1_loss_16: 0.2150 - dense_1_loss_17: 0.2015 - dense_1_loss_18: 0.2006 - dense_1_loss_19: 0.2088 - dense_1_loss_20: 0.2182 - dense_1_loss_21: 0.2181 - dense_1_loss_22: 0.2291 - dense_1_loss_23: 0.2054 - dense_1_loss_24: 0.1950 - dense_1_loss_25: 0.2023 - dense_1_loss_26: 0.2065 - dense_1_loss_27: 0.2064 - dense_1_loss_28: 0.2084 - dense_1_loss_29: 0.2424 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4500 - dense_1_acc_3: 0.7167 - dense_1_acc_4: 0.9333 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 0.9833 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 47/100
60/60 [==============================] - 0s - loss: 13.1148 - dense_1_loss_1: 3.9308 - dense_1_loss_2: 2.2489 - dense_1_loss_3: 1.1232 - dense_1_loss_4: 0.5273 - dense_1_loss_5: 0.4214 - dense_1_loss_6: 0.2922 - dense_1_loss_7: 0.2527 - dense_1_loss_8: 0.2677 - dense_1_loss_9: 0.2289 - dense_1_loss_10: 0.1980 - dense_1_loss_11: 0.1871 - dense_1_loss_12: 0.1862 - dense_1_loss_13: 0.1581 - dense_1_loss_14: 0.1695 - dense_1_loss_15: 0.1860 - dense_1_loss_16: 0.1968 - dense_1_loss_17: 0.1852 - dense_1_loss_18: 0.1874 - dense_1_loss_19: 0.1962 - dense_1_loss_20: 0.1951 - dense_1_loss_21: 0.2001 - dense_1_loss_22: 0.2128 - dense_1_loss_23: 0.1888 - dense_1_loss_24: 0.1837 - dense_1_loss_25: 0.1860 - dense_1_loss_26: 0.1913 - dense_1_loss_27: 0.1876 - dense_1_loss_28: 0.1936 - dense_1_loss_29: 0.2320 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4500 - dense_1_acc_3: 0.7167 - dense_1_acc_4: 0.9333 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 0.9833 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 48/100
60/60 [==============================] - 0s - loss: 12.6318 - dense_1_loss_1: 3.9262 - dense_1_loss_2: 2.2099 - dense_1_loss_3: 1.0895 - dense_1_loss_4: 0.4896 - dense_1_loss_5: 0.4001 - dense_1_loss_6: 0.2706 - dense_1_loss_7: 0.2349 - dense_1_loss_8: 0.2505 - dense_1_loss_9: 0.2116 - dense_1_loss_10: 0.1837 - dense_1_loss_11: 0.1738 - dense_1_loss_12: 0.1717 - dense_1_loss_13: 0.1454 - dense_1_loss_14: 0.1566 - dense_1_loss_15: 0.1731 - dense_1_loss_16: 0.1892 - dense_1_loss_17: 0.1747 - dense_1_loss_18: 0.1738 - dense_1_loss_19: 0.1739 - dense_1_loss_20: 0.1918 - dense_1_loss_21: 0.1875 - dense_1_loss_22: 0.1921 - dense_1_loss_23: 0.1768 - dense_1_loss_24: 0.1735 - dense_1_loss_25: 0.1730 - dense_1_loss_26: 0.1742 - dense_1_loss_27: 0.1708 - dense_1_loss_28: 0.1801 - dense_1_loss_29: 0.2131 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4500 - dense_1_acc_3: 0.7167 - dense_1_acc_4: 0.9333 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 49/100
60/60 [==============================] - 0s - loss: 12.1718 - dense_1_loss_1: 3.9215 - dense_1_loss_2: 2.1729 - dense_1_loss_3: 1.0545 - dense_1_loss_4: 0.4604 - dense_1_loss_5: 0.3774 - dense_1_loss_6: 0.2551 - dense_1_loss_7: 0.2169 - dense_1_loss_8: 0.2355 - dense_1_loss_9: 0.1968 - dense_1_loss_10: 0.1711 - dense_1_loss_11: 0.1628 - dense_1_loss_12: 0.1605 - dense_1_loss_13: 0.1337 - dense_1_loss_14: 0.1497 - dense_1_loss_15: 0.1597 - dense_1_loss_16: 0.1731 - dense_1_loss_17: 0.1620 - dense_1_loss_18: 0.1598 - dense_1_loss_19: 0.1623 - dense_1_loss_20: 0.1768 - dense_1_loss_21: 0.1707 - dense_1_loss_22: 0.1779 - dense_1_loss_23: 0.1638 - dense_1_loss_24: 0.1547 - dense_1_loss_25: 0.1583 - dense_1_loss_26: 0.1618 - dense_1_loss_27: 0.1599 - dense_1_loss_28: 0.1698 - dense_1_loss_29: 0.1925 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4667 - dense_1_acc_3: 0.7167 - dense_1_acc_4: 0.9500 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 50/100
60/60 [==============================] - 0s - loss: 11.7745 - dense_1_loss_1: 3.9164 - dense_1_loss_2: 2.1374 - dense_1_loss_3: 1.0221 - dense_1_loss_4: 0.4324 - dense_1_loss_5: 0.3553 - dense_1_loss_6: 0.2423 - dense_1_loss_7: 0.2020 - dense_1_loss_8: 0.2207 - dense_1_loss_9: 0.1821 - dense_1_loss_10: 0.1589 - dense_1_loss_11: 0.1547 - dense_1_loss_12: 0.1494 - dense_1_loss_13: 0.1259 - dense_1_loss_14: 0.1409 - dense_1_loss_15: 0.1477 - dense_1_loss_16: 0.1597 - dense_1_loss_17: 0.1506 - dense_1_loss_18: 0.1494 - dense_1_loss_19: 0.1538 - dense_1_loss_20: 0.1608 - dense_1_loss_21: 0.1567 - dense_1_loss_22: 0.1697 - dense_1_loss_23: 0.1504 - dense_1_loss_24: 0.1428 - dense_1_loss_25: 0.1458 - dense_1_loss_26: 0.1507 - dense_1_loss_27: 0.1518 - dense_1_loss_28: 0.1605 - dense_1_loss_29: 0.1837 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4667 - dense_1_acc_3: 0.7333 - dense_1_acc_4: 0.9667 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 0.9833 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 51/100

60/60 [==============================] - 0s - loss: 11.3880 - dense_1_loss_1: 3.9117 - dense_1_loss_2: 2.1017 - dense_1_loss_3: 0.9920 - dense_1_loss_4: 0.4068 - dense_1_loss_5: 0.3347 - dense_1_loss_6: 0.2283 - dense_1_loss_7: 0.1894 - dense_1_loss_8: 0.2050 - dense_1_loss_9: 0.1717 - dense_1_loss_10: 0.1482 - dense_1_loss_11: 0.1431 - dense_1_loss_12: 0.1400 - dense_1_loss_13: 0.1170 - dense_1_loss_14: 0.1278 - dense_1_loss_15: 0.1397 - dense_1_loss_16: 0.1477 - dense_1_loss_17: 0.1394 - dense_1_loss_18: 0.1404 - dense_1_loss_19: 0.1418 - dense_1_loss_20: 0.1491 - dense_1_loss_21: 0.1466 - dense_1_loss_22: 0.1570 - dense_1_loss_23: 0.1387 - dense_1_loss_24: 0.1329 - dense_1_loss_25: 0.1353 - dense_1_loss_26: 0.1410 - dense_1_loss_27: 0.1383 - dense_1_loss_28: 0.1486 - dense_1_loss_29: 0.1741 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4667 - dense_1_acc_3: 0.7333 - dense_1_acc_4: 0.9667 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 52/100
60/60 [==============================] - 0s - loss: 11.0451 - dense_1_loss_1: 3.9075 - dense_1_loss_2: 2.0684 - dense_1_loss_3: 0.9613 - dense_1_loss_4: 0.3824 - dense_1_loss_5: 0.3176 - dense_1_loss_6: 0.2141 - dense_1_loss_7: 0.1787 - dense_1_loss_8: 0.1927 - dense_1_loss_9: 0.1602 - dense_1_loss_10: 0.1374 - dense_1_loss_11: 0.1334 - dense_1_loss_12: 0.1303 - dense_1_loss_13: 0.1080 - dense_1_loss_14: 0.1177 - dense_1_loss_15: 0.1314 - dense_1_loss_16: 0.1422 - dense_1_loss_17: 0.1312 - dense_1_loss_18: 0.1307 - dense_1_loss_19: 0.1295 - dense_1_loss_20: 0.1455 - dense_1_loss_21: 0.1397 - dense_1_loss_22: 0.1435 - dense_1_loss_23: 0.1312 - dense_1_loss_24: 0.1252 - dense_1_loss_25: 0.1279 - dense_1_loss_26: 0.1302 - dense_1_loss_27: 0.1289 - dense_1_loss_28: 0.1367 - dense_1_loss_29: 0.1618 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4667 - dense_1_acc_3: 0.7500 - dense_1_acc_4: 0.9667 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 0.9833 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 53/100
60/60 [==============================] - 0s - loss: 10.7255 - dense_1_loss_1: 3.9028 - dense_1_loss_2: 2.0355 - dense_1_loss_3: 0.9332 - dense_1_loss_4: 0.3612 - dense_1_loss_5: 0.3010 - dense_1_loss_6: 0.2020 - dense_1_loss_7: 0.1674 - dense_1_loss_8: 0.1824 - dense_1_loss_9: 0.1493 - dense_1_loss_10: 0.1282 - dense_1_loss_11: 0.1256 - dense_1_loss_12: 0.1215 - dense_1_loss_13: 0.1007 - dense_1_loss_14: 0.1110 - dense_1_loss_15: 0.1228 - dense_1_loss_16: 0.1314 - dense_1_loss_17: 0.1221 - dense_1_loss_18: 0.1213 - dense_1_loss_19: 0.1226 - dense_1_loss_20: 0.1333 - dense_1_loss_21: 0.1301 - dense_1_loss_22: 0.1336 - dense_1_loss_23: 0.1234 - dense_1_loss_24: 0.1173 - dense_1_loss_25: 0.1210 - dense_1_loss_26: 0.1213 - dense_1_loss_27: 0.1220 - dense_1_loss_28: 0.1304 - dense_1_loss_29: 0.1511 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.4667 - dense_1_acc_3: 0.7667 - dense_1_acc_4: 0.9833 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 0.9833 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 54/100
60/60 [==============================] - 0s - loss: 10.4308 - dense_1_loss_1: 3.8984 - dense_1_loss_2: 2.0043 - dense_1_loss_3: 0.9071 - dense_1_loss_4: 0.3419 - dense_1_loss_5: 0.2845 - dense_1_loss_6: 0.1912 - dense_1_loss_7: 0.1562 - dense_1_loss_8: 0.1720 - dense_1_loss_9: 0.1384 - dense_1_loss_10: 0.1207 - dense_1_loss_11: 0.1197 - dense_1_loss_12: 0.1138 - dense_1_loss_13: 0.0951 - dense_1_loss_14: 0.1053 - dense_1_loss_15: 0.1145 - dense_1_loss_16: 0.1219 - dense_1_loss_17: 0.1131 - dense_1_loss_18: 0.1139 - dense_1_loss_19: 0.1173 - dense_1_loss_20: 0.1215 - dense_1_loss_21: 0.1213 - dense_1_loss_22: 0.1262 - dense_1_loss_23: 0.1139 - dense_1_loss_24: 0.1083 - dense_1_loss_25: 0.1128 - dense_1_loss_26: 0.1131 - dense_1_loss_27: 0.1169 - dense_1_loss_28: 0.1239 - dense_1_loss_29: 0.1435 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5000 - dense_1_acc_3: 0.7667 - dense_1_acc_4: 0.9833 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 55/100
60/60 [==============================] - 0s - loss: 10.1644 - dense_1_loss_1: 3.8940 - dense_1_loss_2: 1.9722 - dense_1_loss_3: 0.8814 - dense_1_loss_4: 0.3247 - dense_1_loss_5: 0.2720 - dense_1_loss_6: 0.1820 - dense_1_loss_7: 0.1488 - dense_1_loss_8: 0.1636 - dense_1_loss_9: 0.1312 - dense_1_loss_10: 0.1142 - dense_1_loss_11: 0.1127 - dense_1_loss_12: 0.1074 - dense_1_loss_13: 0.0906 - dense_1_loss_14: 0.0985 - dense_1_loss_15: 0.1072 - dense_1_loss_16: 0.1143 - dense_1_loss_17: 0.1058 - dense_1_loss_18: 0.1078 - dense_1_loss_19: 0.1107 - dense_1_loss_20: 0.1141 - dense_1_loss_21: 0.1151 - dense_1_loss_22: 0.1180 - dense_1_loss_23: 0.1059 - dense_1_loss_24: 0.1014 - dense_1_loss_25: 0.1054 - dense_1_loss_26: 0.1058 - dense_1_loss_27: 0.1080 - dense_1_loss_28: 0.1160 - dense_1_loss_29: 0.1356 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5000 - dense_1_acc_3: 0.7833 - dense_1_acc_4: 0.9833 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 56/100

60/60 [==============================] - 0s - loss: 9.9057 - dense_1_loss_1: 3.8901 - dense_1_loss_2: 1.9436 - dense_1_loss_3: 0.8554 - dense_1_loss_4: 0.3075 - dense_1_loss_5: 0.2571 - dense_1_loss_6: 0.1722 - dense_1_loss_7: 0.1403 - dense_1_loss_8: 0.1516 - dense_1_loss_9: 0.1247 - dense_1_loss_10: 0.1069 - dense_1_loss_11: 0.1055 - dense_1_loss_12: 0.1011 - dense_1_loss_13: 0.0850 - dense_1_loss_14: 0.0924 - dense_1_loss_15: 0.1012 - dense_1_loss_16: 0.1089 - dense_1_loss_17: 0.1003 - dense_1_loss_18: 0.1011 - dense_1_loss_19: 0.1031 - dense_1_loss_20: 0.1100 - dense_1_loss_21: 0.1086 - dense_1_loss_22: 0.1099 - dense_1_loss_23: 0.0996 - dense_1_loss_24: 0.0957 - dense_1_loss_25: 0.0984 - dense_1_loss_26: 0.0997 - dense_1_loss_27: 0.0994 - dense_1_loss_28: 0.1078 - dense_1_loss_29: 0.1286 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5000 - dense_1_acc_3: 0.8167 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 57/100
60/60 [==============================] - 0s - loss: 9.6742 - dense_1_loss_1: 3.8859 - dense_1_loss_2: 1.9136 - dense_1_loss_3: 0.8325 - dense_1_loss_4: 0.2914 - dense_1_loss_5: 0.2443 - dense_1_loss_6: 0.1644 - dense_1_loss_7: 0.1318 - dense_1_loss_8: 0.1428 - dense_1_loss_9: 0.1184 - dense_1_loss_10: 0.0995 - dense_1_loss_11: 0.1000 - dense_1_loss_12: 0.0959 - dense_1_loss_13: 0.0797 - dense_1_loss_14: 0.0877 - dense_1_loss_15: 0.0951 - dense_1_loss_16: 0.1029 - dense_1_loss_17: 0.0950 - dense_1_loss_18: 0.0954 - dense_1_loss_19: 0.0966 - dense_1_loss_20: 0.1038 - dense_1_loss_21: 0.1032 - dense_1_loss_22: 0.1032 - dense_1_loss_23: 0.0953 - dense_1_loss_24: 0.0905 - dense_1_loss_25: 0.0929 - dense_1_loss_26: 0.0943 - dense_1_loss_27: 0.0945 - dense_1_loss_28: 0.1020 - dense_1_loss_29: 0.1216 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5000 - dense_1_acc_3: 0.8333 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00      
Epoch 58/100
60/60 [==============================] - 0s - loss: 9.4606 - dense_1_loss_1: 3.8816 - dense_1_loss_2: 1.8853 - dense_1_loss_3: 0.8119 - dense_1_loss_4: 0.2781 - dense_1_loss_5: 0.2327 - dense_1_loss_6: 0.1563 - dense_1_loss_7: 0.1249 - dense_1_loss_8: 0.1356 - dense_1_loss_9: 0.1111 - dense_1_loss_10: 0.0939 - dense_1_loss_11: 0.0952 - dense_1_loss_12: 0.0906 - dense_1_loss_13: 0.0754 - dense_1_loss_14: 0.0830 - dense_1_loss_15: 0.0901 - dense_1_loss_16: 0.0965 - dense_1_loss_17: 0.0898 - dense_1_loss_18: 0.0899 - dense_1_loss_19: 0.0922 - dense_1_loss_20: 0.0970 - dense_1_loss_21: 0.0970 - dense_1_loss_22: 0.0979 - dense_1_loss_23: 0.0898 - dense_1_loss_24: 0.0851 - dense_1_loss_25: 0.0877 - dense_1_loss_26: 0.0895 - dense_1_loss_27: 0.0903 - dense_1_loss_28: 0.0969 - dense_1_loss_29: 0.1154 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5000 - dense_1_acc_3: 0.8333 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 59/100
60/60 [==============================] - 0s - loss: 9.2557 - dense_1_loss_1: 3.8779 - dense_1_loss_2: 1.8585 - dense_1_loss_3: 0.7895 - dense_1_loss_4: 0.2658 - dense_1_loss_5: 0.2219 - dense_1_loss_6: 0.1489 - dense_1_loss_7: 0.1180 - dense_1_loss_8: 0.1297 - dense_1_loss_9: 0.1051 - dense_1_loss_10: 0.0897 - dense_1_loss_11: 0.0900 - dense_1_loss_12: 0.0860 - dense_1_loss_13: 0.0716 - dense_1_loss_14: 0.0782 - dense_1_loss_15: 0.0861 - dense_1_loss_16: 0.0906 - dense_1_loss_17: 0.0850 - dense_1_loss_18: 0.0854 - dense_1_loss_19: 0.0873 - dense_1_loss_20: 0.0909 - dense_1_loss_21: 0.0910 - dense_1_loss_22: 0.0927 - dense_1_loss_23: 0.0839 - dense_1_loss_24: 0.0795 - dense_1_loss_25: 0.0826 - dense_1_loss_26: 0.0837 - dense_1_loss_27: 0.0863 - dense_1_loss_28: 0.0916 - dense_1_loss_29: 0.1083 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5000 - dense_1_acc_3: 0.8333 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 60/100
60/60 [==============================] - 0s - loss: 9.0696 - dense_1_loss_1: 3.8739 - dense_1_loss_2: 1.8319 - dense_1_loss_3: 0.7692 - dense_1_loss_4: 0.2545 - dense_1_loss_5: 0.2113 - dense_1_loss_6: 0.1417 - dense_1_loss_7: 0.1127 - dense_1_loss_8: 0.1228 - dense_1_loss_9: 0.0997 - dense_1_loss_10: 0.0857 - dense_1_loss_11: 0.0851 - dense_1_loss_12: 0.0820 - dense_1_loss_13: 0.0679 - dense_1_loss_14: 0.0737 - dense_1_loss_15: 0.0824 - dense_1_loss_16: 0.0861 - dense_1_loss_17: 0.0810 - dense_1_loss_18: 0.0815 - dense_1_loss_19: 0.0826 - dense_1_loss_20: 0.0871 - dense_1_loss_21: 0.0860 - dense_1_loss_22: 0.0883 - dense_1_loss_23: 0.0788 - dense_1_loss_24: 0.0750 - dense_1_loss_25: 0.0783 - dense_1_loss_26: 0.0790 - dense_1_loss_27: 0.0813 - dense_1_loss_28: 0.0871 - dense_1_loss_29: 0.1029 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5167 - dense_1_acc_3: 0.8500 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 61/100

60/60 [==============================] - 0s - loss: 8.8944 - dense_1_loss_1: 3.8698 - dense_1_loss_2: 1.8066 - dense_1_loss_3: 0.7494 - dense_1_loss_4: 0.2427 - dense_1_loss_5: 0.2028 - dense_1_loss_6: 0.1351 - dense_1_loss_7: 0.1078 - dense_1_loss_8: 0.1171 - dense_1_loss_9: 0.0952 - dense_1_loss_10: 0.0813 - dense_1_loss_11: 0.0811 - dense_1_loss_12: 0.0780 - dense_1_loss_13: 0.0642 - dense_1_loss_14: 0.0703 - dense_1_loss_15: 0.0780 - dense_1_loss_16: 0.0816 - dense_1_loss_17: 0.0775 - dense_1_loss_18: 0.0773 - dense_1_loss_19: 0.0778 - dense_1_loss_20: 0.0830 - dense_1_loss_21: 0.0815 - dense_1_loss_22: 0.0835 - dense_1_loss_23: 0.0751 - dense_1_loss_24: 0.0715 - dense_1_loss_25: 0.0745 - dense_1_loss_26: 0.0750 - dense_1_loss_27: 0.0770 - dense_1_loss_28: 0.0828 - dense_1_loss_29: 0.0970 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5167 - dense_1_acc_3: 0.8500 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 0.9833 - dense_1_acc_30: 0.0000e+00     
Epoch 62/100
60/60 [==============================] - 0s - loss: 8.7344 - dense_1_loss_1: 3.8660 - dense_1_loss_2: 1.7812 - dense_1_loss_3: 0.7314 - dense_1_loss_4: 0.2328 - dense_1_loss_5: 0.1936 - dense_1_loss_6: 0.1290 - dense_1_loss_7: 0.1027 - dense_1_loss_8: 0.1111 - dense_1_loss_9: 0.0901 - dense_1_loss_10: 0.0772 - dense_1_loss_11: 0.0778 - dense_1_loss_12: 0.0740 - dense_1_loss_13: 0.0609 - dense_1_loss_14: 0.0677 - dense_1_loss_15: 0.0743 - dense_1_loss_16: 0.0775 - dense_1_loss_17: 0.0740 - dense_1_loss_18: 0.0735 - dense_1_loss_19: 0.0743 - dense_1_loss_20: 0.0787 - dense_1_loss_21: 0.0781 - dense_1_loss_22: 0.0792 - dense_1_loss_23: 0.0726 - dense_1_loss_24: 0.0683 - dense_1_loss_25: 0.0711 - dense_1_loss_26: 0.0714 - dense_1_loss_27: 0.0736 - dense_1_loss_28: 0.0796 - dense_1_loss_29: 0.0928 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5167 - dense_1_acc_3: 0.8500 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 63/100
60/60 [==============================] - 0s - loss: 8.5807 - dense_1_loss_1: 3.8624 - dense_1_loss_2: 1.7576 - dense_1_loss_3: 0.7130 - dense_1_loss_4: 0.2234 - dense_1_loss_5: 0.1846 - dense_1_loss_6: 0.1237 - dense_1_loss_7: 0.0981 - dense_1_loss_8: 0.1060 - dense_1_loss_9: 0.0857 - dense_1_loss_10: 0.0732 - dense_1_loss_11: 0.0743 - dense_1_loss_12: 0.0704 - dense_1_loss_13: 0.0581 - dense_1_loss_14: 0.0648 - dense_1_loss_15: 0.0708 - dense_1_loss_16: 0.0739 - dense_1_loss_17: 0.0702 - dense_1_loss_18: 0.0701 - dense_1_loss_19: 0.0706 - dense_1_loss_20: 0.0747 - dense_1_loss_21: 0.0745 - dense_1_loss_22: 0.0751 - dense_1_loss_23: 0.0696 - dense_1_loss_24: 0.0650 - dense_1_loss_25: 0.0675 - dense_1_loss_26: 0.0682 - dense_1_loss_27: 0.0704 - dense_1_loss_28: 0.0761 - dense_1_loss_29: 0.0890 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5333 - dense_1_acc_3: 0.8500 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 64/100
60/60 [==============================] - 0s - loss: 8.4329 - dense_1_loss_1: 3.8585 - dense_1_loss_2: 1.7348 - dense_1_loss_3: 0.6947 - dense_1_loss_4: 0.2150 - dense_1_loss_5: 0.1763 - dense_1_loss_6: 0.1176 - dense_1_loss_7: 0.0937 - dense_1_loss_8: 0.1014 - dense_1_loss_9: 0.0814 - dense_1_loss_10: 0.0699 - dense_1_loss_11: 0.0706 - dense_1_loss_12: 0.0671 - dense_1_loss_13: 0.0558 - dense_1_loss_14: 0.0617 - dense_1_loss_15: 0.0676 - dense_1_loss_16: 0.0708 - dense_1_loss_17: 0.0667 - dense_1_loss_18: 0.0672 - dense_1_loss_19: 0.0674 - dense_1_loss_20: 0.0716 - dense_1_loss_21: 0.0704 - dense_1_loss_22: 0.0715 - dense_1_loss_23: 0.0659 - dense_1_loss_24: 0.0620 - dense_1_loss_25: 0.0642 - dense_1_loss_26: 0.0648 - dense_1_loss_27: 0.0667 - dense_1_loss_28: 0.0725 - dense_1_loss_29: 0.0848 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5667 - dense_1_acc_3: 0.8500 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 65/100
60/60 [==============================] - 0s - loss: 8.3012 - dense_1_loss_1: 3.8550 - dense_1_loss_2: 1.7121 - dense_1_loss_3: 0.6791 - dense_1_loss_4: 0.2075 - dense_1_loss_5: 0.1691 - dense_1_loss_6: 0.1133 - dense_1_loss_7: 0.0899 - dense_1_loss_8: 0.0970 - dense_1_loss_9: 0.0780 - dense_1_loss_10: 0.0670 - dense_1_loss_11: 0.0674 - dense_1_loss_12: 0.0643 - dense_1_loss_13: 0.0537 - dense_1_loss_14: 0.0589 - dense_1_loss_15: 0.0650 - dense_1_loss_16: 0.0683 - dense_1_loss_17: 0.0638 - dense_1_loss_18: 0.0645 - dense_1_loss_19: 0.0646 - dense_1_loss_20: 0.0689 - dense_1_loss_21: 0.0672 - dense_1_loss_22: 0.0685 - dense_1_loss_23: 0.0627 - dense_1_loss_24: 0.0593 - dense_1_loss_25: 0.0613 - dense_1_loss_26: 0.0616 - dense_1_loss_27: 0.0634 - dense_1_loss_28: 0.0690 - dense_1_loss_29: 0.0806 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5667 - dense_1_acc_3: 0.8500 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 66/100

60/60 [==============================] - 0s - loss: 8.1717 - dense_1_loss_1: 3.8514 - dense_1_loss_2: 1.6904 - dense_1_loss_3: 0.6630 - dense_1_loss_4: 0.1997 - dense_1_loss_5: 0.1615 - dense_1_loss_6: 0.1088 - dense_1_loss_7: 0.0863 - dense_1_loss_8: 0.0928 - dense_1_loss_9: 0.0747 - dense_1_loss_10: 0.0640 - dense_1_loss_11: 0.0644 - dense_1_loss_12: 0.0616 - dense_1_loss_13: 0.0514 - dense_1_loss_14: 0.0566 - dense_1_loss_15: 0.0620 - dense_1_loss_16: 0.0655 - dense_1_loss_17: 0.0610 - dense_1_loss_18: 0.0617 - dense_1_loss_19: 0.0619 - dense_1_loss_20: 0.0660 - dense_1_loss_21: 0.0643 - dense_1_loss_22: 0.0654 - dense_1_loss_23: 0.0600 - dense_1_loss_24: 0.0567 - dense_1_loss_25: 0.0586 - dense_1_loss_26: 0.0587 - dense_1_loss_27: 0.0608 - dense_1_loss_28: 0.0660 - dense_1_loss_29: 0.0766 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5667 - dense_1_acc_3: 0.8500 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 67/100
60/60 [==============================] - 0s - loss: 8.0535 - dense_1_loss_1: 3.8476 - dense_1_loss_2: 1.6686 - dense_1_loss_3: 0.6485 - dense_1_loss_4: 0.1926 - dense_1_loss_5: 0.1557 - dense_1_loss_6: 0.1050 - dense_1_loss_7: 0.0828 - dense_1_loss_8: 0.0891 - dense_1_loss_9: 0.0719 - dense_1_loss_10: 0.0613 - dense_1_loss_11: 0.0621 - dense_1_loss_12: 0.0593 - dense_1_loss_13: 0.0492 - dense_1_loss_14: 0.0548 - dense_1_loss_15: 0.0591 - dense_1_loss_16: 0.0626 - dense_1_loss_17: 0.0584 - dense_1_loss_18: 0.0590 - dense_1_loss_19: 0.0596 - dense_1_loss_20: 0.0626 - dense_1_loss_21: 0.0616 - dense_1_loss_22: 0.0627 - dense_1_loss_23: 0.0578 - dense_1_loss_24: 0.0543 - dense_1_loss_25: 0.0562 - dense_1_loss_26: 0.0563 - dense_1_loss_27: 0.0586 - dense_1_loss_28: 0.0637 - dense_1_loss_29: 0.0726 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5667 - dense_1_acc_3: 0.8500 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 68/100
60/60 [==============================] - 0s - loss: 7.9409 - dense_1_loss_1: 3.8440 - dense_1_loss_2: 1.6480 - dense_1_loss_3: 0.6336 - dense_1_loss_4: 0.1857 - dense_1_loss_5: 0.1494 - dense_1_loss_6: 0.1009 - dense_1_loss_7: 0.0797 - dense_1_loss_8: 0.0854 - dense_1_loss_9: 0.0687 - dense_1_loss_10: 0.0587 - dense_1_loss_11: 0.0600 - dense_1_loss_12: 0.0570 - dense_1_loss_13: 0.0471 - dense_1_loss_14: 0.0528 - dense_1_loss_15: 0.0567 - dense_1_loss_16: 0.0598 - dense_1_loss_17: 0.0561 - dense_1_loss_18: 0.0567 - dense_1_loss_19: 0.0575 - dense_1_loss_20: 0.0598 - dense_1_loss_21: 0.0593 - dense_1_loss_22: 0.0603 - dense_1_loss_23: 0.0557 - dense_1_loss_24: 0.0522 - dense_1_loss_25: 0.0539 - dense_1_loss_26: 0.0543 - dense_1_loss_27: 0.0566 - dense_1_loss_28: 0.0612 - dense_1_loss_29: 0.0699 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5667 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 0.9833 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 69/100
60/60 [==============================] - 0s - loss: 7.8319 - dense_1_loss_1: 3.8405 - dense_1_loss_2: 1.6281 - dense_1_loss_3: 0.6197 - dense_1_loss_4: 0.1795 - dense_1_loss_5: 0.1429 - dense_1_loss_6: 0.0967 - dense_1_loss_7: 0.0769 - dense_1_loss_8: 0.0816 - dense_1_loss_9: 0.0657 - dense_1_loss_10: 0.0564 - dense_1_loss_11: 0.0575 - dense_1_loss_12: 0.0547 - dense_1_loss_13: 0.0450 - dense_1_loss_14: 0.0506 - dense_1_loss_15: 0.0548 - dense_1_loss_16: 0.0576 - dense_1_loss_17: 0.0540 - dense_1_loss_18: 0.0546 - dense_1_loss_19: 0.0549 - dense_1_loss_20: 0.0575 - dense_1_loss_21: 0.0569 - dense_1_loss_22: 0.0579 - dense_1_loss_23: 0.0533 - dense_1_loss_24: 0.0503 - dense_1_loss_25: 0.0518 - dense_1_loss_26: 0.0521 - dense_1_loss_27: 0.0542 - dense_1_loss_28: 0.0585 - dense_1_loss_29: 0.0674 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5667 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 70/100
60/60 [==============================] - 0s - loss: 7.7306 - dense_1_loss_1: 3.8371 - dense_1_loss_2: 1.6078 - dense_1_loss_3: 0.6059 - dense_1_loss_4: 0.1739 - dense_1_loss_5: 0.1379 - dense_1_loss_6: 0.0933 - dense_1_loss_7: 0.0744 - dense_1_loss_8: 0.0785 - dense_1_loss_9: 0.0633 - dense_1_loss_10: 0.0545 - dense_1_loss_11: 0.0552 - dense_1_loss_12: 0.0525 - dense_1_loss_13: 0.0434 - dense_1_loss_14: 0.0485 - dense_1_loss_15: 0.0530 - dense_1_loss_16: 0.0556 - dense_1_loss_17: 0.0521 - dense_1_loss_18: 0.0527 - dense_1_loss_19: 0.0527 - dense_1_loss_20: 0.0557 - dense_1_loss_21: 0.0545 - dense_1_loss_22: 0.0558 - dense_1_loss_23: 0.0510 - dense_1_loss_24: 0.0484 - dense_1_loss_25: 0.0497 - dense_1_loss_26: 0.0500 - dense_1_loss_27: 0.0520 - dense_1_loss_28: 0.0562 - dense_1_loss_29: 0.0652 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5667 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 71/100

60/60 [==============================] - 0s - loss: 7.6342 - dense_1_loss_1: 3.8336 - dense_1_loss_2: 1.5892 - dense_1_loss_3: 0.5930 - dense_1_loss_4: 0.1679 - dense_1_loss_5: 0.1327 - dense_1_loss_6: 0.0900 - dense_1_loss_7: 0.0720 - dense_1_loss_8: 0.0758 - dense_1_loss_9: 0.0608 - dense_1_loss_10: 0.0527 - dense_1_loss_11: 0.0533 - dense_1_loss_12: 0.0507 - dense_1_loss_13: 0.0419 - dense_1_loss_14: 0.0466 - dense_1_loss_15: 0.0513 - dense_1_loss_16: 0.0537 - dense_1_loss_17: 0.0502 - dense_1_loss_18: 0.0508 - dense_1_loss_19: 0.0507 - dense_1_loss_20: 0.0537 - dense_1_loss_21: 0.0524 - dense_1_loss_22: 0.0537 - dense_1_loss_23: 0.0490 - dense_1_loss_24: 0.0465 - dense_1_loss_25: 0.0478 - dense_1_loss_26: 0.0482 - dense_1_loss_27: 0.0498 - dense_1_loss_28: 0.0539 - dense_1_loss_29: 0.0625 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5667 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 72/100
60/60 [==============================] - 0s - loss: 7.5410 - dense_1_loss_1: 3.8304 - dense_1_loss_2: 1.5698 - dense_1_loss_3: 0.5803 - dense_1_loss_4: 0.1632 - dense_1_loss_5: 0.1278 - dense_1_loss_6: 0.0868 - dense_1_loss_7: 0.0694 - dense_1_loss_8: 0.0730 - dense_1_loss_9: 0.0585 - dense_1_loss_10: 0.0508 - dense_1_loss_11: 0.0514 - dense_1_loss_12: 0.0487 - dense_1_loss_13: 0.0406 - dense_1_loss_14: 0.0450 - dense_1_loss_15: 0.0494 - dense_1_loss_16: 0.0518 - dense_1_loss_17: 0.0483 - dense_1_loss_18: 0.0488 - dense_1_loss_19: 0.0490 - dense_1_loss_20: 0.0515 - dense_1_loss_21: 0.0506 - dense_1_loss_22: 0.0516 - dense_1_loss_23: 0.0473 - dense_1_loss_24: 0.0449 - dense_1_loss_25: 0.0460 - dense_1_loss_26: 0.0463 - dense_1_loss_27: 0.0481 - dense_1_loss_28: 0.0521 - dense_1_loss_29: 0.0595 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5667 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 73/100
60/60 [==============================] - 0s - loss: 7.4558 - dense_1_loss_1: 3.8268 - dense_1_loss_2: 1.5521 - dense_1_loss_3: 0.5690 - dense_1_loss_4: 0.1582 - dense_1_loss_5: 0.1236 - dense_1_loss_6: 0.0839 - dense_1_loss_7: 0.0670 - dense_1_loss_8: 0.0704 - dense_1_loss_9: 0.0564 - dense_1_loss_10: 0.0490 - dense_1_loss_11: 0.0497 - dense_1_loss_12: 0.0471 - dense_1_loss_13: 0.0394 - dense_1_loss_14: 0.0436 - dense_1_loss_15: 0.0478 - dense_1_loss_16: 0.0500 - dense_1_loss_17: 0.0466 - dense_1_loss_18: 0.0470 - dense_1_loss_19: 0.0475 - dense_1_loss_20: 0.0495 - dense_1_loss_21: 0.0488 - dense_1_loss_22: 0.0497 - dense_1_loss_23: 0.0459 - dense_1_loss_24: 0.0434 - dense_1_loss_25: 0.0444 - dense_1_loss_26: 0.0446 - dense_1_loss_27: 0.0465 - dense_1_loss_28: 0.0505 - dense_1_loss_29: 0.0571 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5833 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00         
Epoch 74/100
60/60 [==============================] - 0s - loss: 7.3710 - dense_1_loss_1: 3.8234 - dense_1_loss_2: 1.5347 - dense_1_loss_3: 0.5570 - dense_1_loss_4: 0.1536 - dense_1_loss_5: 0.1186 - dense_1_loss_6: 0.0808 - dense_1_loss_7: 0.0647 - dense_1_loss_8: 0.0677 - dense_1_loss_9: 0.0542 - dense_1_loss_10: 0.0472 - dense_1_loss_11: 0.0480 - dense_1_loss_12: 0.0455 - dense_1_loss_13: 0.0381 - dense_1_loss_14: 0.0421 - dense_1_loss_15: 0.0462 - dense_1_loss_16: 0.0484 - dense_1_loss_17: 0.0451 - dense_1_loss_18: 0.0454 - dense_1_loss_19: 0.0460 - dense_1_loss_20: 0.0478 - dense_1_loss_21: 0.0472 - dense_1_loss_22: 0.0479 - dense_1_loss_23: 0.0444 - dense_1_loss_24: 0.0421 - dense_1_loss_25: 0.0429 - dense_1_loss_26: 0.0432 - dense_1_loss_27: 0.0450 - dense_1_loss_28: 0.0486 - dense_1_loss_29: 0.0550 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5833 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 75/100
60/60 [==============================] - 0s - loss: 7.2930 - dense_1_loss_1: 3.8203 - dense_1_loss_2: 1.5170 - dense_1_loss_3: 0.5457 - dense_1_loss_4: 0.1494 - dense_1_loss_5: 0.1147 - dense_1_loss_6: 0.0781 - dense_1_loss_7: 0.0628 - dense_1_loss_8: 0.0655 - dense_1_loss_9: 0.0526 - dense_1_loss_10: 0.0456 - dense_1_loss_11: 0.0463 - dense_1_loss_12: 0.0441 - dense_1_loss_13: 0.0367 - dense_1_loss_14: 0.0407 - dense_1_loss_15: 0.0448 - dense_1_loss_16: 0.0469 - dense_1_loss_17: 0.0436 - dense_1_loss_18: 0.0440 - dense_1_loss_19: 0.0445 - dense_1_loss_20: 0.0464 - dense_1_loss_21: 0.0457 - dense_1_loss_22: 0.0464 - dense_1_loss_23: 0.0429 - dense_1_loss_24: 0.0408 - dense_1_loss_25: 0.0414 - dense_1_loss_26: 0.0419 - dense_1_loss_27: 0.0436 - dense_1_loss_28: 0.0470 - dense_1_loss_29: 0.0535 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5833 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 76/100

60/60 [==============================] - 0s - loss: 7.2167 - dense_1_loss_1: 3.8171 - dense_1_loss_2: 1.5002 - dense_1_loss_3: 0.5346 - dense_1_loss_4: 0.1454 - dense_1_loss_5: 0.1109 - dense_1_loss_6: 0.0756 - dense_1_loss_7: 0.0608 - dense_1_loss_8: 0.0635 - dense_1_loss_9: 0.0508 - dense_1_loss_10: 0.0442 - dense_1_loss_11: 0.0449 - dense_1_loss_12: 0.0427 - dense_1_loss_13: 0.0356 - dense_1_loss_14: 0.0395 - dense_1_loss_15: 0.0434 - dense_1_loss_16: 0.0455 - dense_1_loss_17: 0.0422 - dense_1_loss_18: 0.0426 - dense_1_loss_19: 0.0429 - dense_1_loss_20: 0.0452 - dense_1_loss_21: 0.0442 - dense_1_loss_22: 0.0448 - dense_1_loss_23: 0.0415 - dense_1_loss_24: 0.0395 - dense_1_loss_25: 0.0400 - dense_1_loss_26: 0.0405 - dense_1_loss_27: 0.0420 - dense_1_loss_28: 0.0452 - dense_1_loss_29: 0.0516 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.5833 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 77/100
60/60 [==============================] - 0s - loss: 7.1467 - dense_1_loss_1: 3.8139 - dense_1_loss_2: 1.4842 - dense_1_loss_3: 0.5246 - dense_1_loss_4: 0.1415 - dense_1_loss_5: 0.1078 - dense_1_loss_6: 0.0734 - dense_1_loss_7: 0.0591 - dense_1_loss_8: 0.0617 - dense_1_loss_9: 0.0493 - dense_1_loss_10: 0.0428 - dense_1_loss_11: 0.0436 - dense_1_loss_12: 0.0414 - dense_1_loss_13: 0.0344 - dense_1_loss_14: 0.0384 - dense_1_loss_15: 0.0422 - dense_1_loss_16: 0.0440 - dense_1_loss_17: 0.0408 - dense_1_loss_18: 0.0413 - dense_1_loss_19: 0.0416 - dense_1_loss_20: 0.0437 - dense_1_loss_21: 0.0427 - dense_1_loss_22: 0.0433 - dense_1_loss_23: 0.0402 - dense_1_loss_24: 0.0382 - dense_1_loss_25: 0.0387 - dense_1_loss_26: 0.0393 - dense_1_loss_27: 0.0407 - dense_1_loss_28: 0.0437 - dense_1_loss_29: 0.0499 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6000 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 78/100
60/60 [==============================] - 0s - loss: 7.0769 - dense_1_loss_1: 3.8105 - dense_1_loss_2: 1.4683 - dense_1_loss_3: 0.5146 - dense_1_loss_4: 0.1379 - dense_1_loss_5: 0.1042 - dense_1_loss_6: 0.0711 - dense_1_loss_7: 0.0573 - dense_1_loss_8: 0.0596 - dense_1_loss_9: 0.0477 - dense_1_loss_10: 0.0415 - dense_1_loss_11: 0.0422 - dense_1_loss_12: 0.0401 - dense_1_loss_13: 0.0334 - dense_1_loss_14: 0.0374 - dense_1_loss_15: 0.0407 - dense_1_loss_16: 0.0426 - dense_1_loss_17: 0.0396 - dense_1_loss_18: 0.0400 - dense_1_loss_19: 0.0404 - dense_1_loss_20: 0.0421 - dense_1_loss_21: 0.0414 - dense_1_loss_22: 0.0420 - dense_1_loss_23: 0.0390 - dense_1_loss_24: 0.0371 - dense_1_loss_25: 0.0374 - dense_1_loss_26: 0.0381 - dense_1_loss_27: 0.0395 - dense_1_loss_28: 0.0425 - dense_1_loss_29: 0.0486 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6000 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 79/100
60/60 [==============================] - 0s - loss: 7.0088 - dense_1_loss_1: 3.8077 - dense_1_loss_2: 1.4530 - dense_1_loss_3: 0.5035 - dense_1_loss_4: 0.1345 - dense_1_loss_5: 0.1008 - dense_1_loss_6: 0.0686 - dense_1_loss_7: 0.0555 - dense_1_loss_8: 0.0577 - dense_1_loss_9: 0.0460 - dense_1_loss_10: 0.0403 - dense_1_loss_11: 0.0410 - dense_1_loss_12: 0.0388 - dense_1_loss_13: 0.0324 - dense_1_loss_14: 0.0363 - dense_1_loss_15: 0.0395 - dense_1_loss_16: 0.0413 - dense_1_loss_17: 0.0384 - dense_1_loss_18: 0.0388 - dense_1_loss_19: 0.0392 - dense_1_loss_20: 0.0406 - dense_1_loss_21: 0.0402 - dense_1_loss_22: 0.0408 - dense_1_loss_23: 0.0379 - dense_1_loss_24: 0.0360 - dense_1_loss_25: 0.0363 - dense_1_loss_26: 0.0369 - dense_1_loss_27: 0.0384 - dense_1_loss_28: 0.0414 - dense_1_loss_29: 0.0470 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6000 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 80/100
60/60 [==============================] - 0s - loss: 6.9461 - dense_1_loss_1: 3.8044 - dense_1_loss_2: 1.4378 - dense_1_loss_3: 0.4946 - dense_1_loss_4: 0.1313 - dense_1_loss_5: 0.0982 - dense_1_loss_6: 0.0667 - dense_1_loss_7: 0.0541 - dense_1_loss_8: 0.0560 - dense_1_loss_9: 0.0448 - dense_1_loss_10: 0.0392 - dense_1_loss_11: 0.0398 - dense_1_loss_12: 0.0377 - dense_1_loss_13: 0.0315 - dense_1_loss_14: 0.0353 - dense_1_loss_15: 0.0384 - dense_1_loss_16: 0.0400 - dense_1_loss_17: 0.0373 - dense_1_loss_18: 0.0377 - dense_1_loss_19: 0.0381 - dense_1_loss_20: 0.0393 - dense_1_loss_21: 0.0391 - dense_1_loss_22: 0.0396 - dense_1_loss_23: 0.0368 - dense_1_loss_24: 0.0350 - dense_1_loss_25: 0.0352 - dense_1_loss_26: 0.0357 - dense_1_loss_27: 0.0372 - dense_1_loss_28: 0.0402 - dense_1_loss_29: 0.0453 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6000 - dense_1_acc_3: 0.8667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00         
Epoch 81/100

60/60 [==============================] - 0s - loss: 6.8848 - dense_1_loss_1: 3.8013 - dense_1_loss_2: 1.4231 - dense_1_loss_3: 0.4849 - dense_1_loss_4: 0.1283 - dense_1_loss_5: 0.0953 - dense_1_loss_6: 0.0645 - dense_1_loss_7: 0.0526 - dense_1_loss_8: 0.0542 - dense_1_loss_9: 0.0434 - dense_1_loss_10: 0.0381 - dense_1_loss_11: 0.0386 - dense_1_loss_12: 0.0366 - dense_1_loss_13: 0.0306 - dense_1_loss_14: 0.0342 - dense_1_loss_15: 0.0373 - dense_1_loss_16: 0.0389 - dense_1_loss_17: 0.0362 - dense_1_loss_18: 0.0367 - dense_1_loss_19: 0.0370 - dense_1_loss_20: 0.0383 - dense_1_loss_21: 0.0381 - dense_1_loss_22: 0.0385 - dense_1_loss_23: 0.0358 - dense_1_loss_24: 0.0340 - dense_1_loss_25: 0.0343 - dense_1_loss_26: 0.0346 - dense_1_loss_27: 0.0362 - dense_1_loss_28: 0.0392 - dense_1_loss_29: 0.0441 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6000 - dense_1_acc_3: 0.9000 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 82/100
60/60 [==============================] - 0s - loss: 6.8274 - dense_1_loss_1: 3.7982 - dense_1_loss_2: 1.4089 - dense_1_loss_3: 0.4763 - dense_1_loss_4: 0.1254 - dense_1_loss_5: 0.0930 - dense_1_loss_6: 0.0628 - dense_1_loss_7: 0.0513 - dense_1_loss_8: 0.0527 - dense_1_loss_9: 0.0422 - dense_1_loss_10: 0.0371 - dense_1_loss_11: 0.0375 - dense_1_loss_12: 0.0356 - dense_1_loss_13: 0.0298 - dense_1_loss_14: 0.0332 - dense_1_loss_15: 0.0364 - dense_1_loss_16: 0.0379 - dense_1_loss_17: 0.0352 - dense_1_loss_18: 0.0357 - dense_1_loss_19: 0.0359 - dense_1_loss_20: 0.0374 - dense_1_loss_21: 0.0370 - dense_1_loss_22: 0.0373 - dense_1_loss_23: 0.0347 - dense_1_loss_24: 0.0331 - dense_1_loss_25: 0.0333 - dense_1_loss_26: 0.0336 - dense_1_loss_27: 0.0351 - dense_1_loss_28: 0.0379 - dense_1_loss_29: 0.0428 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6000 - dense_1_acc_3: 0.9167 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 83/100
60/60 [==============================] - 0s - loss: 6.7692 - dense_1_loss_1: 3.7953 - dense_1_loss_2: 1.3942 - dense_1_loss_3: 0.4672 - dense_1_loss_4: 0.1224 - dense_1_loss_5: 0.0903 - dense_1_loss_6: 0.0609 - dense_1_loss_7: 0.0498 - dense_1_loss_8: 0.0510 - dense_1_loss_9: 0.0410 - dense_1_loss_10: 0.0360 - dense_1_loss_11: 0.0364 - dense_1_loss_12: 0.0347 - dense_1_loss_13: 0.0290 - dense_1_loss_14: 0.0323 - dense_1_loss_15: 0.0355 - dense_1_loss_16: 0.0369 - dense_1_loss_17: 0.0343 - dense_1_loss_18: 0.0347 - dense_1_loss_19: 0.0349 - dense_1_loss_20: 0.0364 - dense_1_loss_21: 0.0359 - dense_1_loss_22: 0.0362 - dense_1_loss_23: 0.0338 - dense_1_loss_24: 0.0322 - dense_1_loss_25: 0.0323 - dense_1_loss_26: 0.0327 - dense_1_loss_27: 0.0342 - dense_1_loss_28: 0.0368 - dense_1_loss_29: 0.0417 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6000 - dense_1_acc_3: 0.9167 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 84/100
60/60 [==============================] - 0s - loss: 6.7151 - dense_1_loss_1: 3.7922 - dense_1_loss_2: 1.3800 - dense_1_loss_3: 0.4591 - dense_1_loss_4: 0.1197 - dense_1_loss_5: 0.0879 - dense_1_loss_6: 0.0593 - dense_1_loss_7: 0.0485 - dense_1_loss_8: 0.0496 - dense_1_loss_9: 0.0399 - dense_1_loss_10: 0.0351 - dense_1_loss_11: 0.0354 - dense_1_loss_12: 0.0338 - dense_1_loss_13: 0.0283 - dense_1_loss_14: 0.0315 - dense_1_loss_15: 0.0346 - dense_1_loss_16: 0.0359 - dense_1_loss_17: 0.0333 - dense_1_loss_18: 0.0338 - dense_1_loss_19: 0.0340 - dense_1_loss_20: 0.0353 - dense_1_loss_21: 0.0349 - dense_1_loss_22: 0.0353 - dense_1_loss_23: 0.0330 - dense_1_loss_24: 0.0314 - dense_1_loss_25: 0.0314 - dense_1_loss_26: 0.0318 - dense_1_loss_27: 0.0334 - dense_1_loss_28: 0.0359 - dense_1_loss_29: 0.0407 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6000 - dense_1_acc_3: 0.9167 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 85/100
60/60 [==============================] - 0s - loss: 6.6631 - dense_1_loss_1: 3.7892 - dense_1_loss_2: 1.3673 - dense_1_loss_3: 0.4505 - dense_1_loss_4: 0.1171 - dense_1_loss_5: 0.0856 - dense_1_loss_6: 0.0577 - dense_1_loss_7: 0.0472 - dense_1_loss_8: 0.0483 - dense_1_loss_9: 0.0388 - dense_1_loss_10: 0.0341 - dense_1_loss_11: 0.0345 - dense_1_loss_12: 0.0329 - dense_1_loss_13: 0.0276 - dense_1_loss_14: 0.0307 - dense_1_loss_15: 0.0337 - dense_1_loss_16: 0.0349 - dense_1_loss_17: 0.0325 - dense_1_loss_18: 0.0330 - dense_1_loss_19: 0.0332 - dense_1_loss_20: 0.0344 - dense_1_loss_21: 0.0340 - dense_1_loss_22: 0.0344 - dense_1_loss_23: 0.0322 - dense_1_loss_24: 0.0306 - dense_1_loss_25: 0.0306 - dense_1_loss_26: 0.0310 - dense_1_loss_27: 0.0326 - dense_1_loss_28: 0.0350 - dense_1_loss_29: 0.0396 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6167 - dense_1_acc_3: 0.9167 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 86/100

60/60 [==============================] - 0s - loss: 6.6128 - dense_1_loss_1: 3.7865 - dense_1_loss_2: 1.3536 - dense_1_loss_3: 0.4424 - dense_1_loss_4: 0.1147 - dense_1_loss_5: 0.0835 - dense_1_loss_6: 0.0563 - dense_1_loss_7: 0.0461 - dense_1_loss_8: 0.0470 - dense_1_loss_9: 0.0378 - dense_1_loss_10: 0.0333 - dense_1_loss_11: 0.0337 - dense_1_loss_12: 0.0321 - dense_1_loss_13: 0.0269 - dense_1_loss_14: 0.0300 - dense_1_loss_15: 0.0329 - dense_1_loss_16: 0.0341 - dense_1_loss_17: 0.0317 - dense_1_loss_18: 0.0321 - dense_1_loss_19: 0.0323 - dense_1_loss_20: 0.0335 - dense_1_loss_21: 0.0331 - dense_1_loss_22: 0.0336 - dense_1_loss_23: 0.0314 - dense_1_loss_24: 0.0299 - dense_1_loss_25: 0.0298 - dense_1_loss_26: 0.0302 - dense_1_loss_27: 0.0318 - dense_1_loss_28: 0.0341 - dense_1_loss_29: 0.0386 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.0667 - dense_1_acc_2: 0.6167 - dense_1_acc_3: 0.9167 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
Epoch 87/100
60/60 [==============================] - 0s - loss: 6.5654 - dense_1_loss_1: 3.7832 - dense_1_loss_2: 1.3415 - dense_1_loss_3: 0.4353 - dense_1_loss_4: 0.1123 - dense_1_loss_5: 0.0817 - dense_1_loss_6: 0.0550 - dense_1_loss_7: 0.0450 - dense_1_loss_8: 0.0459 - dense_1_loss_9: 0.0369 - dense_1_loss_10: 0.0325 - dense_1_loss_11: 0.0329 - dense_1_loss_12: 0.0313 - dense_1_loss_13: 0.0262 - dense_1_loss_14: 0.0293 - dense_1_loss_15: 0.0320 - dense_1_loss_16: 0.0332 - dense_1_loss_17: 0.0309 - dense_1_loss_18: 0.0313 - dense_1_loss_19: 0.0315 - dense_1_loss_20: 0.0327 - dense_1_loss_21: 0.0322 - dense_1_loss_22: 0.0327 - dense_1_loss_23: 0.0307 - dense_1_loss_24: 0.0292 - dense_1_loss_25: 0.0291 - dense_1_loss_26: 0.0294 - dense_1_loss_27: 0.0309 - dense_1_loss_28: 0.0332 - dense_1_loss_29: 0.0375 - dense_1_loss_30: 0.0000e+00 - dense_1_a