2.9线性表应用—一元多项式的表示及相加
2.9线性表应用—一元多项式的表示及相加
前面学习了线性表的概念、顺序存储方式和链式存储方式,本节课我们来 学习线性表应用。本节通过一元多项式的表示及相加的问题,作为线性表应用 的典型,总结了本章学习的线性表的两种存储方式、运算实现技术等主要内 容。
1、一元多项式的表示
一元多项式可按升幂的形式写成:
Pn(x) = p0+p1xe1+p2xe2+…+pnxen,
其中,ei为第 i项的指数,pi是指数 ei的项的系数,(且 1≤e1≤e2≤…≤en)
在计算机内,Pn(x)可以用一个线性表 P来表示:
P= (p0,p1,p2, …,pn )
设有两个一元多项式 Pn(x) 和 Qm(x),假设 m
2、一元多项式的存储
一元多项式的操作可以利用线性表来处理。因此,一元多项式也有顺序存储和链式存储两种方法。‘
一元多项式的顺序存储表示
对于一元多项式:
Pn(x) = p0+p1xe1+p2xe2+…+pnxen
有两种顺序存储方式:
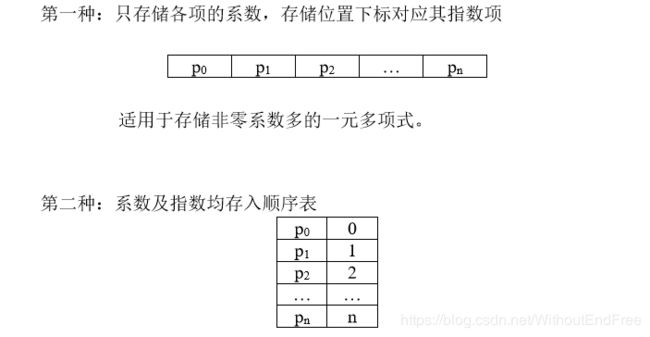
适用于存储非零项少且指数高的一元多项式,此时只存储非零项的系数 和指数即可。
例如:R(x)=1+5x10000+7x20000 (10000和20000为指数)
一元多项式的链式存储表示
struct Polynode
{
int coef;
int exp;
Polynode *next;
} Polynode , * Polylist;
例:建立一元多项式链式存储算法
【算法思想】通过键盘输入一组多项式的系数和指数,用尾插法建立一元 多项式的链表。以输入系数 0 为结束标志,并约定建立多项式链表时,总 是按指数从小到大的顺序排列。
【算法描述】
Polylist polycreate()
{
Polynode *head, *rear, *s;
int c,e;
head=(Polynode *)malloc(sizeof(Polynode)); /*建立多项 式的头结点*/
rear=head; /* rear 始终指向单链表的尾,便于尾插法建表*/
scanf(“%d,%d”,&c,&e);/*键入多项式的系数和指数项*/
while(c!=0) /*若 c=0,则代表多项式的输入结束*/
{
s=(Polynode*)malloc(sizeof(Polynode)); /*申请新 的结点*/
s->coef=c;
s->exp=e;
rear->next=s; /*在当前表尾做插入*/
rear=s;
scanf(“%d,%d”,&c,&e);
}
rear->next=NULL; /*将表的最后一个结点的 next 置 NULL,以示表结束*/
return(head);
}
一元多项式的相加运算
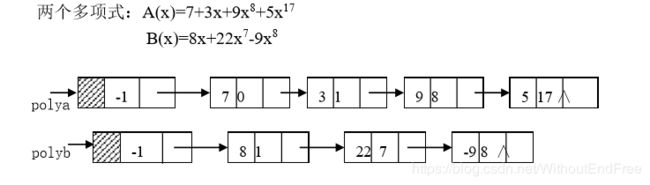
用单链表表示的两个一元多项式
(2)多项式相加的运算规则
为了保证“和多项式”中各项仍按升幂排列,在两个多项式中:
①指数相同项的对应系数相加,若和不为零,则构成“和多项式”中的一项; ②指数不相同的项仍按升幂顺序复抄到“和多项式”中。
【算法思想】
以单链表 polya 和 polyb 分别表示两个一元多项式 A 和 B, A+B 的求和运算,就等同于单链表的插入问题(将单链表 polyb 中的结点插入到单链表 polya中),因此 “和多项式“中的结点无需另生成。
为实现处理,设 p、q 分别指向单链表 polya 和 polyb 的当前项,比较 p、q 结点的指数项,由此得到下列运算规则:
① 若 p->exp< q->exp,则结点 p所指的结点应是“和多项式”中的 一项,令指针 p后移;
② 若 p->exp=q->exp,则将两个结点中的系数相加,当和不为零时 修改结点 p的系数域,释放 q结点;若和为零,则和多项式中无此项,从 A中 删去 p结点,同时释放 p和 q结点。
③ 若 p->exp>q->exp,则结点 q所指的结点应是“和多项式”中的 一项,将结点 q插入在结点 p之前,且令指针 q在原来的链表上后移;
【算法描述】
void polyadd(Polylist polya, Polylist polyb)
/*将两个多项式相加,然后将和多项式存放在多项式 polya 中,并将多项式 ployb删除*/
{
Polynode * p, *q, *tail;
*temp;
int sum;
p=polya->next ; /*令 p和 q分别指向 polya和 polyb多项式链表中的第一个 结点*/
q=polyb->next ;
tail=polya; /* tail指向和多项式的尾结点*/
while(p!=NULL && q!=NULL) /*当两个多项式均未扫描结束时*/
{
if(p->exp< q->exp) /*规则⑴:如果 p指向的多项式项的指数小于 q的指数,将 p结点加入到和 多项式中*/
{
tail ->next=p;
tail =p;
p=p->next;
}
else if(p->exp= =q->exp) /*规则⑵:若指数相等,则相应的系数相加*/
{
sum=p->coef + q->coef;
if (sum!=0) /*若系数和非零,则系数和置入结点 p,释放结点 q,并 将指针后移*/
{
p->coef=sum;
tail ->next=p;
tail =p;
p=p->next;
temp=q; q=q->next;
free(temp);
}
else
{
temp=p;
p=p->next;
free(temp); /*若系数和为零,则删除结点 p与 q,并将指针指向下一个结点*/
temp=q ; q=q->next;
free(temp);
}
}
else
{
tail ->next=q;
tail =q; /*规则⑶:将 q结点加入到“和多项式中”*/
q =q->next;
}
}
if(p!=NULL) /*多项式 A 中还有剩余,则将剩余的结点加入到和多项式 中*/
tail ->next=p;
else /*否则,将 B 中的结点加入到和多项式中*/
tail ->next=q;
}
假设 A 多项式有 M 项,B 多项式有 N 项,则上述算法的时间复杂度为 O(M+N)
推广: 通过对多项式加法的介绍,可以将其推广到实现两个多项式的相乘,因为 乘法可以分解为一系列的加法运算。