为什么自己编的两帧之间视觉里程计用KITTI数据集评估，结果会如此得差呢？

背景介绍

学习了一段时间的SLAM，感觉对它的原理有了一定的了解，就想编写一个两帧之间的运动评估的demo，在这个demo中没有后端优化、建图和回环检测，只有两帧之间的运动估计。大概思路：采用双目相机，利用SGBM算法得到左目的视差图，进而恢复左目的深度信息，前后帧之间采用ORB特征匹配，采用RANSAC算法做误匹配剔除，采用奇异值分解的ICP方法来估计运动。
代码写好了之后，利用KITTI数据集进行验证，采用其Odometry模块中的00序列图片，发现估计的运动结果与KITTI基准值相差挺大的，因此想问问这是咋回事？

代码实现

1.相机的内参

查看KITTI的开发工具包，相机的内参值$f_x,f_y,c_x,c_y$和双目的基线$b$设置如下，
$$f_x=718.856,f_y=718.856,c_x=607.1928,c_y=185.2157$$
$$b=0.54$$

2.视差图的获取

通过Mat GetDisparity(string imgl, string imgr)函数来实现，函数名是GetDisparity，输入参数是imgl和imgr（左图和右图的路径），返回视差图，为Mat类型。函数内容如下：

//获得左右图像的视差
Mat GetDisparity(string imgl, string imgr){
    Mat img_1 = imread(imgl, 0);
    Mat img_2 = imread(imgr, 0);
    cv::Ptr<cv::StereoSGBM> sgbm = cv::StereoSGBM::create(
            0, 96, 9, 8 * 9 * 9, 32 * 9 * 9, 1, 63, 10, 100, 32);    // 神奇的参数
    cv::Mat disparity_sgbm, disparity;
    sgbm->compute(img_1, img_2, disparity_sgbm);
    disparity_sgbm.convertTo(disparity, CV_32F, 1.0 / 16.0f);
    return disparity;
}

此部分代码中的cv::Ptr sgbm = cv::StereoSGBM::create( 0, 96, 9, 8 * 9 * 9, 32 * 9 * 9, 1, 63, 10, 100, 32); // 神奇的参数是参照高翔博士的《视觉SLAM十四讲》书中5.4.1节双目视觉代码写出来的。

3.特征匹配

前后帧通过函数vector qhmatch (string img1, string img2)做特征匹配，函数名是qhmatch，输入参数是img1和img2（上一帧左图和当前帧左图的路径），返回配对的特征点坐标
$$(u_{img1},v_{img1},u_{img2},v_{img2})$$
类型为vector。函数内容如下：

//前后匹配函数
vector<Vector4d> qhmatch (string img1, string img2){
    vector<Vector4d> points;
    Mat img_1 = imread(img1, CV_LOAD_IMAGE_COLOR);
    Mat img_2 = imread(img2, CV_LOAD_IMAGE_COLOR);

    //-- 初始化
    vector<KeyPoint> keypoints_1, keypoints_2;
    Mat descriptors_1, descriptors_2;
    Ptr<FeatureDetector> detector = ORB::create();
    Ptr<DescriptorExtractor> descriptor = ORB::create();
    Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");

    //-- 第一步:检测 Oriented FAST 角点位置
    detector->detect(img_1, keypoints_1);
    detector->detect(img_2, keypoints_2);

    //-- 第二步:根据角点位置计算 BRIEF 描述子
    descriptor->compute(img_1, keypoints_1, descriptors_1);
    descriptor->compute(img_2, keypoints_2, descriptors_2);

    //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
    vector<DMatch> matches;
    matcher->match(descriptors_1, descriptors_2, matches);


    //-- 第四步:匹配点对筛选
    // 计算最小距离和最大距离
    auto min_max = minmax_element(matches.begin(), matches.end(),
                                  [](const DMatch &m1, const DMatch &m2) { return m1.distance < m2.distance; });
    double min_dist = min_max.first->distance;
    double max_dist = min_max.second->distance;
    


    //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
    vector<DMatch> good_matches;
    int i;
    for ( i = 0; i < descriptors_1.rows; i++) {
        if (matches[i].distance <= max(2 * min_dist, 30.0)) {
            good_matches.push_back(matches[i]);
        }
    }

    //保存匹配点对的坐标对应关系
    Vector4d point;
    for (i = 0; i < good_matches.size(); i++){
        point << int(keypoints_1[good_matches[i].queryIdx].pt.x),    int(keypoints_1[good_matches[i].queryIdx].pt.y),
                 int(keypoints_2[good_matches[i].trainIdx].pt.x),    int(keypoints_2[good_matches[i].trainIdx].pt.y);
        points.push_back(point);

    }

    return points;

}

4. 3D点集获取

通过第3步特征匹配，我们获得了配对点的坐标$(u,v)$，但这还不是三维坐标，因此，我们需要把它转换到相机坐标系下，这时利用如下公式，
$$\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\frac{f_{x}b}{d}\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]$$
其中$d$就是第2步视差图的获取中的视差。

5. RANSAC

虽然在特征匹配过程中，我们通过if (matches[i].distance <= max(2 * min_dist, 30.0)) { good_matches.push_back(matches[i]); }排除了一些误匹配值，但任存在误匹配值，因此我们需要通过RANSAC彻底排除误匹配值。RANSAC的算法过程如下图所示

代码实现如下：

        double RANSAC_threshold, RANSAC_iterations;
        RANSAC_iterations = 1000;//设置RANSAC迭代次数
        RANSAC_threshold = 0.1;//设置RANSAC阈值
        vector<Vector6d> inliers_best, inliers_current;
        int number_inliers_best = 0;
        Matrix3d matrix_R_best;
        Matrix<double, 3, 1> matrix_t_best;


        int k;
        for (k = 0; k < RANSAC_iterations; k++){


            int number1,number2,number3,number4;
            number1 = rand() % pointscam.size();
            number2 = rand() % pointscam.size();
            number3 = rand() % pointscam.size();
            number4 = rand() % pointscam.size();

            Vector6d a,b,c,d;
            a = pointscam[number1];
            b = pointscam[number2];
            c = pointscam[number3];
            d = pointscam[number4];
            Matrix<double, 12, 12> matrix_A;
            matrix_A << a(0), a(1), a(2), 0, 0, 0, 0, 0, 0, 1, 0, 0,
                        0, 0, 0, a(0), a(1), a(2), 0, 0, 0, 0, 1, 0,
                        0, 0, 0, 0, 0, 0, a(0), a(1), a(2), 0, 0, 1,
                        b(0), b(1), b(2), 0, 0, 0, 0, 0, 0, 1, 0, 0,
                        0, 0, 0, b(0), b(1), b(2), 0, 0, 0, 0, 1, 0,
                        0, 0, 0, 0, 0, 0, b(0), b(1), b(2), 0, 0, 1,
                        c(0), c(1), c(2), 0, 0, 0, 0, 0, 0, 1, 0, 0,
                        0, 0, 0, c(0), c(1), c(2), 0, 0, 0, 0, 1, 0,
                        0, 0, 0, 0, 0, 0, c(0), c(1), c(2), 0, 0, 1,
                        d(0), d(1), d(2), 0, 0, 0, 0, 0, 0, 1, 0, 0,
                        0, 0, 0, d(0), d(1), d(2), 0, 0, 0, 0, 1, 0,
                        0, 0, 0, 0, 0, 0, d(0), d(1), d(2), 0, 0, 1;
            Matrix<double, 12, 1> matrix_b;
            matrix_b << a(3), a(4), a(5), b(3), b(4), b(5), c(3), c(4), c(5), d(3), d(4), d(5);
            Matrix<double, 12, 1> x = matrix_A.colPivHouseholderQr().solve(matrix_b);
            Matrix3d matrix_R;
            matrix_R << x(0), x(1), x(2),
                        x(3), x(4), x(5),
                        x(6), x(7), x(8);
            Matrix<double, 3, 1> matrix_t;
            matrix_t << x(9), x(10), x(11);

            inliers_current.clear();
            for (int i = 0; i < pointscam.size(); i++) {
                if (i == number1 || i == number2 || i == number3 || i == number4) continue;
                Vector3d delta_location;
                delta_location = Vector3d(pointscam[i](3), pointscam[i](4), pointscam[i](5)) - matrix_R * Vector3d(pointscam[i](0), pointscam[i](1), pointscam[i](2)) - matrix_t;
                double delta_location_norm;
                delta_location_norm = delta_location.norm();
                if (delta_location_norm < RANSAC_threshold) {
                    inliers_current.push_back(pointscam[i]);
                }
            }
            inliers_current.push_back(pointscam[number1]);
            inliers_current.push_back(pointscam[number2]);
            inliers_current.push_back(pointscam[number3]);
            inliers_current.push_back(pointscam[number4]);
            if (inliers_current.size() > number_inliers_best){
                number_inliers_best = inliers_current.size();
                inliers_best.clear();
                inliers_best = inliers_current;
                matrix_R_best = matrix_R;
                matrix_t_best = matrix_t;
            }
        }

其中pointscam为vector>，记录了已匹配的三维点集。

6. ICP估计位姿

在此，我们已经得到了，经过RANSAC之后的已匹配的三维点集，接下来我们用基于奇异值分解的ICP方法来估计位姿，即旋转矩阵$R$和平移向量$t$。此部分代码原理参照高翔《视觉SLAM十四讲》中7.9节 3D-3D：ICP。

        int N = inliers_best.size();
        Vector6d p;
        for (int i = 0; i < N; i++){
            p += inliers_best[i];
        }
        p = p / N;//点集质心
        vector<Vector6d> q(N);
        for(int i = 0; i < N; i++){
            q[i] = inliers_best[i] - p;//去质心化坐标
        }
        Matrix3d W ;
        for (int i = 0; i < N; i++){
            W += Vector3d( q[i](3), q[i](4), q[i](5) ) * Vector3d( q[i](0), q[i](1), q[i](2) ).transpose();
        }
        cout << "W=" << endl;
        cout << W << endl;
        //对W进行奇异值分解
        Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
        Eigen::Matrix3d U = svd.matrixU();
        Eigen::Matrix3d V = svd.matrixV();
        Matrix3d R;
        R = U * V.transpose();
        if (R.determinant() < 0) R = -R;
        Vector3d t;
        t = Vector3d( p(3), p(4), p(5) ) - R * Vector3d( p(0), p(1), p(2) );
        cout << "由ICP得到的旋转矩阵R=\n" << R << endl;
        cout << "由ICP得到的平移向量t=\n" << t << endl;

7. 小结

通过以上6步，我们实现了一个基本的双目两帧之间的视觉里程计！

结果评估

来到问题的关键了，代码写好了之后，我利用KITTI数据集中的Odometry模块00序列中000000.png-000600.png进行效果评估，结果发现效果太差了。我们来对比平移向量$t$：KITTI的真值，此双目两帧之间VO的结果值。



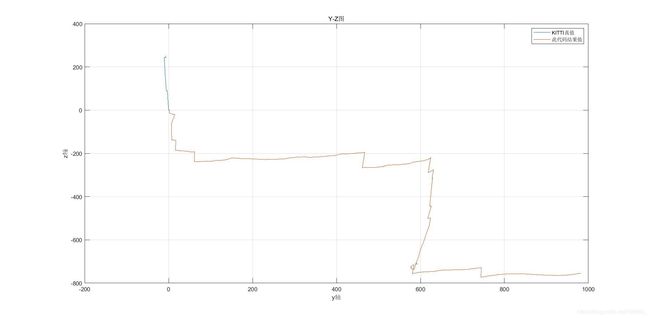
以及000000.png-000010.png的平移向量$t$数值比较，
$$KITTI真值$$
$$\left[\begin{array}{cccccccccc}-0.0469& -0.0468& -0.0469& -0.0468& -0.0469& -0.0468& -0.0469& -0.0468& -0.0469& -0.0469\\ -0.0284& -0.0284& -0.0284& -0.0284& -0.0284& -0.0284& -0.0284& -0.0284& -0.0284& -0.0284\\ 0.8587& 0.8576& 0.8587& 0.8577& 0.8587& 0.8577& 0.8588& 0.8577& 0.8586& 0.8589\end{array}\right]$$
其中每一列都是一个平移向量。
$$此代码结果值$$
$$\left[\begin{array}{cccccccccc}0.5571& 0.9929& 3.9490& 4.9649& 6.9377& 8.2413& 7.9446& 8.9122& 8.3287& 9.1118\\ 1.3609& 0.1563& 1.1231& 0.0765& -0.5173& -0.5405& -0.5820& 0.7446& 0.1349& 0.4579\\ -0.2270& -0.7007& 0.3834& -0.2695& 0.6908& 1.2347& 1.4882& 2.9503& 3.8896& 3.7126\end{array}\right]$$
由以上结果可知，此代码得到的平移矩阵$t$结果太差了，可原因是什么呢？虽说我没有加入后端优化、建图和回环检测，可不应该一开始结果就偏了呀，原因是什么呢？