网络信息安全学习笔记之数论定理
一、素数与单向函数
1.素数
素数是数论的核心
关于素数的基本信息从小学就开始接触，在这里不做赘述
2.单向函数
一个函数f满足下列条件，则称该函数为单向函数
- 对于所有f域的任意x，容易计算y=f(x)
- 对于几乎所有f域的任意y，求一个是y=f(x)成立的x，在计算上几乎不可行
简而言之就是一个函数正向运算简单，逆运算十分困难
3.单向陷阱门函数
一个可逆函数满足下列条件则称之为单项陷阱门函数
- 对于f域的任意x，容易求y=F(x)
- 对于f域的任意y，除非获得暗门信息（附加信息）,否则求解x=
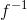(y)在计算上不可行，
4.单向函数举例
①离散对数
令质数p满足p-1含有另一大质数q (q整除p-1)及一整数g, 1
若给定整数x, 求y = gx mod p, 最多需要Llog2x｣+w(x)-1次乘法, w(x)为x中所有1的个数。如x =15, 即
x =(1111)2, w(x)=4, 则g15 =((g2)g)2·g)2·g mod p, 只需要3 + 4 -1=6次乘法。
但是若给定p, g及y, 求x, 则为DLP问题, 最快方法需要L(p)=exp{(lnpln(lnp))½}次运算。
当p=512位时, L(p)约为2256≈1077, 计算上不可行, 因为2100≈1030, 计算要1016年。
②因数分解
给定大素数 p和q, 求n = p×q, 只要一次乘法
给定n, 求p和q, 即为因数分解问题(FAC), 最快方法需要 T(n) = exp {c(ln n ln (ln n))½} 次运算, 其中c为大于1的正整数。若p≈n, 解离散对数比因数分解难。
③背包问题
给定有限个自然数序列集合B=(b1,b2,…bn)及二进制序列x=(x1,x2,…xn), xi∈(0,1), 求S=∑xibi最多只需n-1次加法；但若给定B和S, 求x则非常困难。
穷举时有2n种可能, 当n很大时为计算上不可行。
Garey和Johnson证明, 背包问题是NP问题
5.单向函数的交换性
单向函数本身在密码学中应用不大，但是如果具有交换性，则作用巨大
交换性：令Z为一集合，F为将Z映射到Z本身的函数集合令z∈Z，Fx（z）表示此集合的第x函数，若Fx(Fy(z))=Fy(Fx(z))，则称此函数具有交换性
二、费马定理
1.费马小定理
若p是素数，a是正整数且不能被p整除，则 
mod p =1，即 
mod p=a
证明：
因为{a mod p, 2a mod p, ..., (p-1)a mod p}是{1, 2, ..., (p-1)}的置换形
所以（a x 2a x ...x(p-1)a）mod p = 1x2x3x...(p-1) =（p-1）！
又因为（a x 2a x ...x(p-1)a）= （p-1)! x
所以原式得： (p-1)! x mod p = (p-1)!
约掉阶乘项，得： mod p = 1
例（1）计算
mod 11
根据定理直接可得原式为1
（2）计算
mod 11
2.费马大定理
当整数n >2时，关于x, y, z的方程 x^n + y^n = z^n 没有正整数解
三、欧拉定理
1.欧拉函数
φ(n)是比n小且与n互素的正整数的个数，即模n的缩剩余系中元素之个数
2.欧拉函数的证明
定理：p和q是素数, n=p*q, φ(n)= φ(p)φ(q)=(p-1)(q-1)，即对于素数p，φ(p)=p-1
证明：
考虑余数集合{0, 1, …, (pq-1)}中不与n互素的余数集合是{p, 2p, …, (q-1)p}, {q, 2q, …, (p-1)q}和0,
所以φ(n)= pq-[(q-1)+(p-1)+1]=pq-(p+q)+1= (p-1)(q-1)=φ(p)φ(q)
n为合数时可以分解为素数的乘积
n = 
*
*...*
则
φ(n) = 
3.欧拉定理
对任意互质的a和n有：
mod n = 1,即 ≡ 1 (mod n)
mod n = a ,即 ≡ a (mod n)
4.欧拉定理证明
（1）若 n 是素数，根据欧拉函数和费马小定理，則上式成立；
若p是素数, a是正整数且不能被p整除, 则ap-1 mod p=1
（2）所有小于 n ，且与 n 互质的正整数的集合
即每一个元素都有gcd(xi,n)=1。用a与R中的每个元素模n相乘：
S是R的一个排列，因为
- a与n互素，且xi与n互素，所以axi必与n互素，这样S中所有元素均小于n且与n互素
- S中没有重复元素，所以集合S是集合R的一个置换
四、中国剩余定理
Chinese Remainder Theorem 也称为孙子定理
某一范围内的整数可以通过它对两两互素的整数取模得到的余数重构得到
典型应用就是韩信点兵
今有物不知其数, 三三数之剩二, 五五数之剩三, 七七数之剩二, 问物几何
五、离散对数
幂运算是相对容易的，求解离散对数通常是难解问题
离散对数是包括Diffie-Hellman密钥交换和数字签名(DSA)在内的许多公钥算法的基础
