图像增强—频域增强技术

1. 频域增强原理

在频域中，变换系数反映了某些图像的特征。如频谱的直流分量比例于图像的平均亮度、噪音对应于频率较高的区域、图像实体对应于频率较低的区域

在频谱中，图像中心处对应了图像中变化较平缓的区域，四周对应了图像边缘、噪音或者变化陡峭的部分。因此我们可以将代表了图像边缘、噪音或者变化陡峭的高频率成分滤除掉，只留下变化平缓的低频率成分，再由频域变换回时域，这就相当于对图像进行了平滑处理；相反，若滤去低频率成分，只留下高频率成分，就相当于对图像进行了锐化处理。

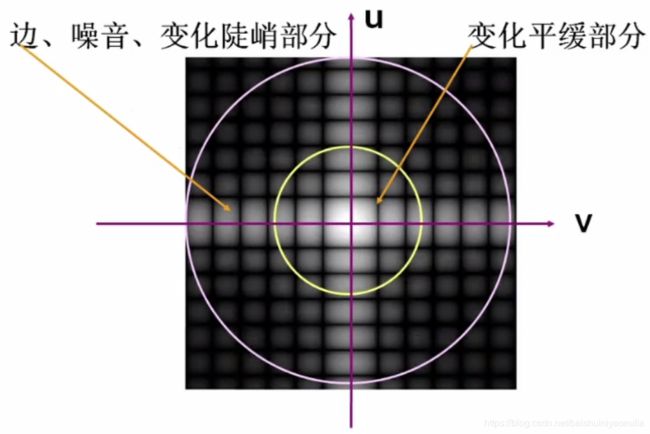可以看出，频域增强的原理十分简单，其应用的重点问题在于滤波半径阈值如何选取。

2. 低通滤波器

有卷积定理，滤波数学表达式为：$$G(\mu ,\nu )=F(\mu ,\nu )H(\mu ,\nu )$$滤波后的图像为：$$G(x,y)=f^{-1}\{G(\mu ,\nu )\}=f^{-1}\{F(\mu ,\nu )H(\mu ,\nu )\}$$其中$H(\mu ,\nu )$即为冲激响应的变换形式，低通滤波器设计的关键就在于$H(\mu ,\nu )$

几种低通滤波器

2.1. 理想圆形低通滤波器 (Ideal Circular Low Pass Filter)

理想圆形低通滤波器是在傅里叶平面上半径为$D$的圆形滤波器，其冲激响应为$$H(\mu ,\nu )=\{\begin{array}{ll}1,& D(\mu ,\nu )⩽D_0\\ 0,& D(\mu ,\nu )⩾D_0\end{array}，D_0为截止频率$$

理论上来说，$D_0$半径内的频率分量无损通过，而圆外的频率分量会被滤除，但由于其自身会产生振铃效应，常常导致实际结果并不理想

振铃效应示意图：
可以看到在空域图像外围有剧烈的震荡

2.2. 巴特沃斯低通滤波器(Butterwoth Low Pass Filter)

巴特沃斯低通滤波器的冲激函数定义为：$$H(\mu ,\nu )=\frac{1}{1+[D(\mu ,\nu )/D_0{]}^{2n}}$$或$$H(\mu ,\nu )=\frac{1}{1+(\sqrt{2}-1)[D(\mu ,\nu )/D_0{]}^{2n}}$$

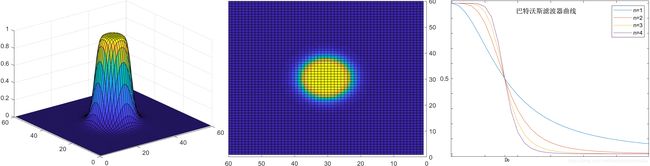
根据图示可以看出，巴特沃斯低通滤波器与理想圆形低通滤波器最大的区别就在于，理想圆形低通滤波器有一个明显的阶跃界限，而巴特沃斯低通滤波器则是平滑变化的过渡带。而且经巴特沃斯低通滤波器处理的图像没有明显的振铃效应，这是过滤器在低频和高频之间平滑过渡的结果。

巴特沃斯低通滤波器的空域图像：
可以与上图理想圆形低通滤波器的空域图像对比，振铃效应减弱很多

2.3. 高斯低通滤波器

高斯低通滤波器的冲激函数定义为：$$H(\mu ,\nu )=e^{-D^2(\mu ,\nu )/2{\sigma }^2}$$
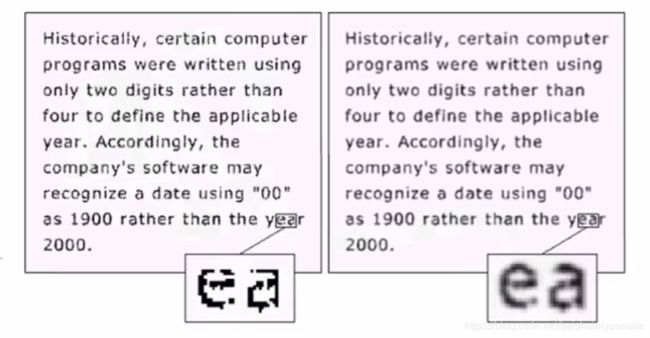
高斯滤波器会把陡峭的图像边缘进行拓展，这样做虽然在一定程度上模糊图像，但却可以平滑图像、增强图像效果，使图像更易于辨认，例如：

3. 高通滤波器

高通滤波器与低通滤波器相对应，其数学表达式为：$$G(\mu ,\nu )=F(\mu ,\nu )H_{HP}(\mu ,\nu )$$其中$H_{HP}(\mu ,\nu )=1-H_{LP}(\mu ,\nu )$，1指的是整个频谱，$H_{LP}(\mu ,\nu )$指的就是低通滤波器

因此，低通滤波器中的常用滤波器经过简单变换之后就可以变为高通滤波器，常用的有：

1. 理想圆形高通滤波器$$H_{HP}(\mu ,\nu )=\{\begin{array}{ll}0,& D(\mu ,\nu )⩽D_0\\ 1,& D(\mu ,\nu )⩾D_0\end{array}，D_0为截止频率$$
2. 巴特沃斯高通滤波器$$H_{HP}(\mu ,\nu )=\frac{1}{1+[D_0/D(\mu ,\nu ){]}^{2n}}$$或$$H_{HP}(\mu ,\nu )=\frac{1}{1+(1-\sqrt{2})[D(\mu ,\nu )/D_0{]}^{2n}}$$
3. 高斯高通滤波器$$H(\mu ,\nu )=1-e^{-D^2(\mu ,\nu )/2{\sigma }^2}$$
4. 指数高通滤波器$$H_{HP}(\mu ,\nu )=e^{-[D_0/D(\mu ,\nu ){]}^n}$$
5. 梯形高通滤波器$$H_{HP}(\mu ,\nu )=\{\begin{array}{ll}0,& D(\mu ,\nu )⩽D_1\\ \frac{D(\mu ,\nu )-D_1}{D_0-D_1},& D_1<D(\mu ,\nu )<D_0\\ 1,& D(\mu ,\nu )⩾D_0\end{array}，D_0为截止频率$$

4. 频域增强与空域增强

频域增强与空域增强在本质上是一致的，在空域增强中，当空域增强模板$h(x,y)$是相对于中心点对称时，其称为空域卷积模板，满足卷积表达式：$$g(\mu ,\nu )=f\ast h=\sum _{x=0}^{N-1}\sum _{y=0}^{M-1}f(x,y)h(\mu -x,\nu -y)$$变换到频域增强的形式只需对$g(\mu ,\nu )$进行傅里叶变换即可

在实践中，空域增强比频域增强更常用，主要是因为其易于实现且执行速度快，频域增强一般用于空域增强难以达成的领域，例如图像压缩等等