27 Deep Belief Network

Deep Belief Network 是Hinton 在2006 年提出的方法，应用在分类问题上的效果明显好过SVM。它的诞生有着重要的意义，这意味着打开了Deep Learning 的大门，把连接主义推上了历史的舞台，给人类带来了希望。

1 Introduction

首先，来看看Deep Belief Network 这个名字的含义，Belief Network 实际上就是Bayes Network（有向图模型），而Deep 的含义就很简单了，代表有很多层。所以，从字面上理解，Deep Belief Network可以认为是有很多层的有向图模型。Deep Belief Network 的概率图模型如下所示：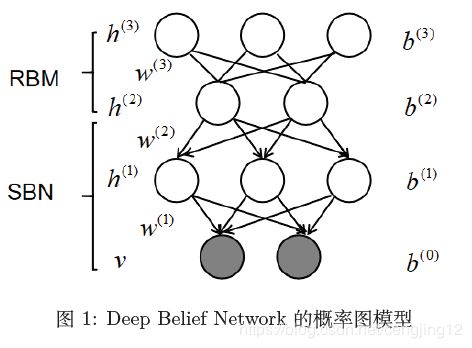
从上述图中，可以看出DBN 是一个混合模型，上面是Restricted Boltzmann Model（RBM）模型，下面是一个Sigmoid Belief Network（SBN）。而每个节点都服从0/1 的伯努利分布，实际上就是一个分层模型。深层的含义，我们将会在下文中描述。注意，这里的$w$ 是用来描述节点直接连接权重的矩阵。

1.1 SBN 简要回顾

Sigmoid Belief Network 的概率图模型如下所示：

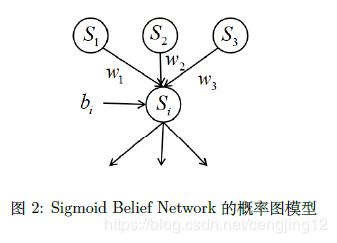
其中，
$$P\left(S_i=1\right)=\frac{1}{1+\exp \left\{b_i+w_1{s}_1+w_2{s}_2+w_3{s}_3\right\}}(1)$$

1.2 DBN 的联合概率分布

在之前的章节我们详细的描述过了，在使用极大似然估计法中基本离不开求联合概率分布。所以，这里需要求DBN 的联合概率分布，而求联合概率分布最终的就是因子分解。那么，我们首先要理顺一下各层之间的依赖关系。显然，v 层只和 $h^{(1)}$ 有关， $h^{(1)}$ 层只和 $h^{(2)},$ 那么有：
$$\begin{array}{rl}P\left(v,h^{(1)},h^{(2)},h^{(3)}\right)& =P\left(v|h^{(1)},h^{(2)},h^{(3)}\right)P\left(h^{(1)},h^{(2)},h^{(3)}\right)\\ & =P\left(v|h^{(1)}\right)P\left(h^{(1)},h^{(2)},h^{(3)}\right)\\ & =P\left(v|h^{(1)}\right)P\left(h^{(1)}|h^{(2)},h^{(3)}\right)P\left(h^{(2)},h^{(3)}\right)\\ & =\prod _{i}P\left(v_i|h^{(1)}\right)\prod _{j}P\left(h_j^{(1)}|h^{(2)},h^{(3)}\right)P\left(h^{(2)},h^{(3)}\right)\end{array}(2)$$
下一步则是将这三个部分分布表示。根据公式 的结论，可以类比的得出：
$$\begin{array}{l}P\left(v_i|h^{(1)}\right)=\mathrm{sigmoid}\left({\left(W_{:,i}^{(1)}\right)}^T\cdot h^{(1)}+b_i^{(0)}\right)\\ P\left(h_j^{(1)}|h^{(2)}\right)=\mathrm{sigmoid}\left({\left(W_{:,j}^{(2)}\right)}^T\cdot h^{(2)}+b_j^{(1)}\right)\end{array}$$
而 $h^{(2)}$ 和 $h^{(3)}$ 之间是 $\mathrm{R}\mathrm{B}\mathrm{M}$ 模型，沿用在 $\mathrm{R}\mathrm{B}\mathrm{M}$ 那一章讲的 Boltzmann Distribution 可以得到：
$$P\left(h^{(2)},h^{(3)}\right)=\frac{1}{Z}\exp \left\{{\left(h^{(3)}\right)}^T{w}^{(3)}{h}^{(2)}+{\left(h^{(2)}\right)}^T{b}^{(2)}+{\left(h^{(3)}\right)}^T{b}^{(3)}\right\}$$
其中参数为：
$$\theta =\left\{W^{(1)},W^{(2)},W^{(3)},b^{(0)},b^{(1)},b^{(2)},b^{(3)}\right\}$$

1.3 小结

本小节，我们讲述了DBN 的Representation，而很多小伙伴会疑惑为什么是一个hybrid model，为什么要一半用有向图，一般用无向图，这样做有什么好处，作者是如何思考出来的，深层含义是什么？这些问题，将在下一节进行描述。

2 DBN 叠加动机

上一节弄清楚了DBN 的model representation，这一小节主要是直觉性的介绍一个DBN 的思路。为什么可以混在一起，为什么Deep Belief Network 可以看成Stacking RBM。我们将从RBM 引出DBN 的模型。

2.1 改进RBM 的原因

首先，我们看看原始的RBM 模型的表达方式，RBM 的求解在“直面配分函数”那章讲到了，是使用对比散度的方法求解。概率图模型如下图所示：

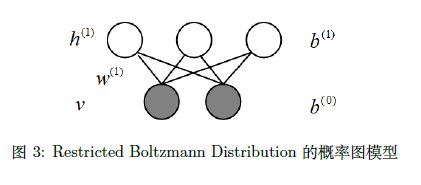
首先，回忆一下当时是如何进行求解的。通过一系列的化简，得到了log likelihood gradient 的表达形式：
$$\begin{array}{rl}\frac{\partial }{\partial w_{ij}}\log P(v)& =\sum _h\sum _{v}P(h,v)\left(-h_i{v}_j\right)-\sum _{h}P(h|v)\left(-h_i{v}_j\right)\\ & =\sum _{h}P(h|v)h_i{v}_j-\sum _h\sum _{v}P(h,v)h_i{v}_j\end{array}(6)$$
但是公式 (6) 的计算过于复杂，斯本是 intractable。所灯提出了用结合梯度上升法的 Gibbs 采样来求 梯度，从而使得 P(v) 的 Log Likelihood 达到最大，公式如下所示：
$$\begin{array}{c}\Delta w_{ij}\leftarrow -\Delta w_{ij}+\frac{\partial }{\partial w_{ij}}\log P(v)\\ \frac{\partial }{\partial w_{ij}}\log P(v)=P\left(h_i=1|v^{(0)}\right)v_j^{(0)}-P\left(h_i=1|v^{(k)}\right)v_j^{(k)}\end{array}$$
那么，按DBN 的叠加方式一定会取得更好的效果吗？结果是不用废话的。需要明确一点，引入RBM是为了探究观测变量的数据结构的关系，其中未观察变量被看作观察变量发生的原因。
所以，模型的关注重点实际上是$v$，而$h$ 不过是我们为了探究$v$ 的数据结构和发生的原因，所做的模型假设而已。$v$ 是没有标签的数据，可以认为是RBM 方法生成的，那么这个RBM 有没有办法改进，让生成的数据更接近真实分布？

2.2 RBM 的改进

根据图 3 可知,
$$P(v)=\sum _{h^{(1)}}P\left(v,h^{(1)}\right)=\sum _{h^{(1)}}P\left(h^{(1)}\right)P\left(v|h^{(1)}\right)$$
通常 $P\left(h^{(1)}\right)$ 看成是 prior 先验， $P\left(v|h^{(1)}\right)$ 则看成是一个生成过程。RBM 在无向图中并没有箭头，无 向图可以看成是一个双向的有向图，如下所示：

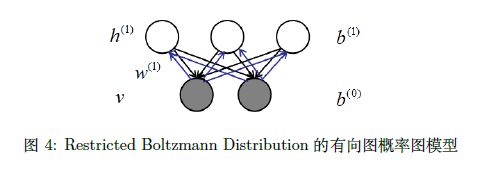
这样，将无向图改写成有向图，可以把概率图分成$h\to v$ 和$v\to h$ 两个过程。两个过程的权重都是一样的。那么假定在RBM 已经学习出来的情况下（$w^{(1)}$ 的参数是确定的），$P(v|h^{(1)})$ 可以看成是$h\to v$，显示是不变得，而$P(h^{(1)})$ 显然也是确定的，和$v\to h$ 过程相关，$w^{(1)}$ 和$v$ 都是确定的。
由于$P(v)={\Sigma }_{h^{(1)}}P(h^{(1)})P(v|h^{(1)})$，$P(h^{(1)})$和$P(v|h^{(1)})$都是确定的，那么P(v) 就是确定的。
那么，可以衍生出一种很自然的想法，可不可以不用$w$ 来表示$P(h^{(1)})$，给$P(h^{(1)})$重新赋一组参数，create 一个新的模型来对$P(h^{(1)})$ 重新建模，用另一个RBM 来表示$P(h^{(1)})$，从而通过提高$P(h^{(1)})$的办法来提高$P(v)$。
那么，怎么学习呢？可以添加一层RBM，这样就可以给P(h(1)) 重新赋一组参数，然后通过新的RBM 参数进行优化的方式来提高$P(h^{(1)})$。如下图所示：

由此，可以认为这样一个模型，比原来的RBM 更好，因为假设$P(v|b^{(1)})$ 是固定的，实际可以优化$P(h^{(1)})$ 来进一步提高模型的性能。同样的思路，可以用同样的办法来优化$P(h^{(2)})$，所以就达到了不停的往上加的效果。
我们希望在训练$h^{(1)}$ 层的时候，希望$v$ 不会对$h^{(1)}$ 造成影响，否则计算复杂度就太高了。所以，就假设在训练KaTeX parse error: Expected '}', got 'EOF' at end of input: h^{(1)的过程中和$v$ 无关，所以概率图模型就变为：

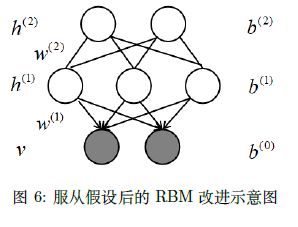
实际上讲解到了这里，DBN 的演变模型大概都已经出来了。我觉得这个系列演变的思路在于关于$P(h^{(1)})$ 和$P(v|h^{(1)})$ 两个部分的计算分开优化，从而发挥最大的效果，尽可能的提高模型的性能。

2.3 为什么DBM 会更好？

下面将给出推导来证明，为什么添加DBM 会使得模型变得更好。首先计算一些RBM 的下界。
$$\begin{array}{rl}\log P(v)& =\log \sum _{h^{(1)}}P\left(v,h^{(1)}\right)\\ & =\log \sum _{h^{(1)}}Q\left(h^{(1)}|v\right)\frac{P\left(v,h^{(1)}\right)}{Q\left(h^{(1)}|v\right)}\\ & =\log {\mathbb{E}}_{Q\left(h^{(1)}|v\right)}\left[\frac{P\left(v,h^{(1)}\right)}{Q\left(h^{(1)}|v\right)}\right]\\ & \ge {\mathbb{E}}_{Q\left(h^{(1)}|v\right)}\log \left[\frac{P\left(v,h^{(1)}\right)}{Q\left(h^{(1)}|v\right)}\right](\text{ 琴生不等式 })\\ & =\sum _{h^{(1)}}Q\left(h^{(1)}|v\right)\left[\log P\left(v,h^{(1)}\right)-\log Q\left(h^{(1)}|v\right)\right]\\ & =\sum _{h^{(1)}}Q\left(h^{(1)}|v\right)\left[\log P\left(v|h^{(1)}\right)+\log P\left(h^{(1)}\right)-\log Q\left(h^{(1)}|v\right)\right]\end{array}$$
那么, ${\sum }_{h^{(1)}}Q\left(h^{(1)}|v\right)\left[\log P\left(v|h^{(1)}\right)+\log P\left(h^{(1)}\right)-\log Q\left(h^{(1)}|v\right)\right]$ 就是原来的 $\mathrm{R}\mathrm{B}\mathrm{M}$ 的下界。在 $\mathrm{R}\mathrm{B}\mathrm{M}$中当整个模型训练完毕之后，$w$ 已经是确定的，那么 $\log P\left(v|h^{(1)}\right)$ 和 $\log Q\left(h^{(1)}|v\right)$ 都可以看成是一个 常数，而 $Q\left(h^{(1)}|v\right)$ 是一个后验。所以下界被我们写为：
$$\sum _{h^{(1)}}Q\left(h^{(1)}|v\right)\log P\left(h^{(1)}\right)+C(11)$$
在 RBM 中 $P\left(h^{(1)}\right)$ 是周定的，而在 DBM 中并不是固定的，而将通过优化 $P\left(h^{(1)}\right)$ 来提升模型的性 能。而 $h^{(2)}$ 的目的就是令 $h^{(1)}$ 的 likelihood 达到最大。那么如果不加层的话，普通的 RBM 中公式(11) 中的所有项都是确定的，而加了层之后，P(h ${}^{(1)}$ ) 不是确定的，而且可以被进一步优化。这样一波操作，就相当于变相的提高了 log $P(v)$ 的 ELBO，而下界增大以后，就等价于可以将 $P(v)$ 的很据的 更高，所以加层以后，模型的性能会更好。 加层以后， $w^{(2)}$ 是需要赋予初始值的，那么令 $w^{(2)}=w^{(1{)}^T}$ 。这样做的意义在于，第二层还没有学 习之前性能就已经达到了不加层时的效果了。那么，可以保证加层之后的模型的性能是有下界的，大于等于原始的 RBM。随着学习的进行，会提高 ELBO 从而获得比 RBM 更好的 P( $v$ )，模型可以得到 更高的 $P(v)$ 就意味着越接近真实分布，性能越好。 在 RBM 中 $P\left(h^{(1)}\right)$ 的参数是由 $w^{(1)}$ 决定的，加层以后 $P\left(h^{(1)}\right)$ 的参数发生了改变是由 $w^{(2)}$ 决定的。

2.4 小结

本节主要讲述的是DBN 的思想来源，为什么DBN 会产生较好的效果。DBN 的主要思路就是通过单独优化先验来提升下界，从而使似然函数最大化，它分离了先验和似然的求解过程，使用两组不同的参数，分开优化，从而获得较好的效果。接下来，将描述其学习过程。

3 贪心逐层预训练

3.1 近似推断的基本思想

本节主要是以一个传统的RBM 的角度来看DBN 的Learning。在上一小节，已经较为详细的论述了，每加一层就会使得ELBO 增加一些。假如，先只引入一个隐藏层$h^{(1)}$，那么有：
$$\begin{array}{rl}\log P(v)& \ge \mathrm{E}\mathrm{L}\mathrm{B}\mathrm{O}\\ & =\sum _{h^{(1)}}Q\left(h^{(1)}|v\right)\left[\log P\left(v,h^{(1)}\right)-\log Q\left(h^{(1)}|v\right)\right]\\ & =\sum _{h^{(1)}}Q\left(h^{(1)}|v\right)\log P\left(v,h^{(1)}\right)-H\left(\log Q\left(h^{(1)}|v\right)\right)\end{array}$$
而 $\log P\left(v,h^{(1)}\right)=\log P\left(v|h^{(1)}\right)+\log P\left(h^{(1)}\right),$ 通过将当层以下层的参数全部固定, 然后新建一个 $\mathrm{R}\mathrm{B}\mathrm{M}$来优化 $P\left(h^{(1)}\right),$ 从而达到优化 ELBO 的目的。
很多同学会好奇，这个 $Q\left(h^{(1)}|v\right)$ 是什么？在前面的近似推断和 $\mathrm{E}\mathrm{M}$ 算法的部分，都做了详细的 描述。Q $\left(h^{(1)}|v\right)$ 是用来近似真实后验 $P\left(h^{(1)}|v\right)$ 的简单分布，当且仅当 $Q\left(h^{(1)}|v\right)=P\left(h^{(1)}|v\right)$ 时等号 成立。但是为什么要近似推断呢?
虽然，在原始的 RBM 中，RBM 的后验是可以计算的。因为在 RBM 的无向图模型中，可观测变量都已知的情况下，不可观测变量之间都是相互独立的，所以，RBM 模型是可分解的，也意味着可降， 低复杂度，后验计算比较简单。
但是,在 DBM 中就不一样了,观察图 1 很容易得出, 当可观测变量 $v$ 被观测时。根据 D-Separation 中的 Head to Head 原则可得 $h^{(1)}$ 中的节点之间都是相互联系的，这个现象也被称作 Explain away 现 象。所以， $P\left(h^{(1)}|v\right)$ 是不可分解的，而且如果层数比较多的话，还要考虑对 $h^{(1)}$ 和 $h^{(2)}$ 求边缘分布, 这个计算基本是 intractable。所以，精确推断是搞不定了，需要用 $Q\left(h^{(1)}|v\right)$ 来近似 $P\left(h^{(1)}|v\right)$

3.2 训练方法

现在的问题是 $Q\left(h^{(1)}|v\right)$ 指的是一个近似分布，但是这个分布怎么求呢？注意，我们采取的逐层训 练的方法，你可以理解是前馈神经网络一样，求对某层求解时，假设其他层的参数都是周定的，不予考虑，从下往上一层一层的训练。
求解的思路是这样的，假设 $v$ 和 $h^{(1)}$ 之间是无向图，那么这两层之间可以看成是一个 RBM，因 为是 RBM 就不存在不可分解的问题，后验计算比较方使，这时 $Q\left(h^{(1)}|v\right)=P\left(h^{(1)}|v\right),$ 可以得到：
$$Q\left(h^{(1)}|v\right)=\prod _{i}Q\left(h_i^{(1)}|v\right)=\prod _i\mathrm{sigmoid}\left(w_{i,i}^{(1)}+b_i^{(1)}\right)$$
利用这个后验分布，可以采样得出 $h^{(1)}$ 层的样本，然后利用同样的办法求得 $h^{(2)}$ 层，这样一层一层的 往上计算。注意到，最上面一层是一个真实的 RBM 了，因为把无问图变成有问图的目的就是为了在 上面加一层，到了最上面一层了，不需要再往上加了，理所应当就保留了无向图结构。

3.3 模型的优缺点

实际上，真实的后验分布$P(h^{(1)}|v)$ 是计算不出来的，我们采用了假设的方法，从而近似的计算了一个分布$Q(h^{(1)}|v)$ 来代替后验分布$P(h^{(1)}|v)$。但是，实际上这两个分布之间的差距还是没那么小。所以，DBN 一个硬伤就是它的ELBO 是比较松散的（loose），那么就收敛性就不太好，收敛速率也可能比较低。
模型的优点是，从上而下进行采样比较简单，在最顶层（假设为第$t$ 层）的RBM 的$w$ 和$b$ 都确定的情况下，通过Gibbs 采样可以得到$h^{(t-1)}$ 层的样本，然后下面的所有层都是有向图模型，有向图模型的采样就相对很简单了，一层一层按照拓扑关系才就可以了。

4 总结

不得不说，老师讲的越来与抽象了，特别是涉及到思维层面的东西不太好理解。但是，确实给我的机器学习的研究生涯带来了不少启发。本章主要是介绍深度置信网络（Deep Belief Network，DBN）。首先介绍的是什么是DBN，DBN 的特点和DBN 的Model Representation；然后介绍了传统的RBM模型的劣势，从而提出了在RBM 模型训练完毕以后，对先验进一步优化的思路来提高下界，所以需要设计一个RBM 来对先验进行优化，这样就得到了DBN 的雏形，同时也充分的表明了DBN 在RBM基础上改进的有效性。最后，介绍了DBN 的逐层固定的训练思路，并且讲述了由于概率图的不可分解性，导致后验计算的非常困难。所以用近似推断的方法来计算后验，但是由于近似分布和真实分布之间有一定的差距，导致算法的下界比较松散，收敛性能一般。但是算法的概率图基本由有向图模型构成，关系比较清晰，所以DBN 算法的采样非常简单。