3月2日 雾霾图像清晰化处理,第1人称相机世界的坐标系,焦距、焦点、调焦、超焦距、视场角、滑动变焦Dolly zooming,相机内参
文章目录
- Retinex理论
- 算法步骤
- pinhole camera
- 1st person camera world
- 定义了第1人称相机世界的坐标系
- 画布距离 距离恰好等于焦距(z坐标等于f )
- 想象一个3D点 他们全都缩到我的相机世界中
- 测量光心位置
- 相机第二重要参数Focal length 焦距
- 变化焦距的过程
- 景深(DOF):超出容许弥散圆的景物清晰度下降
- 关于焦点。
- 关于调焦。
- 关于对焦。
- Hyperfocal distance:超焦距
- Field of view视场角
- 光心和焦距同时发生了改变——滑动变焦 (Dolly zoom)
- Intrinsic Camera Parameter
- 主点移到左上角
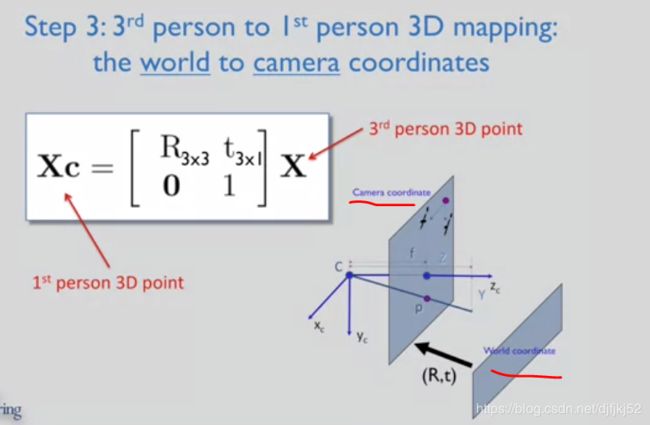
- 3D World to First Person Transformation


Retinex理论
算法步骤


处理过程中,将S(x,y)从时域中变换到频域,将时域的卷积变成频域的相乘 。


![]()

FFT快速傅里叶变换与IFFT快速傅里叶逆变换.
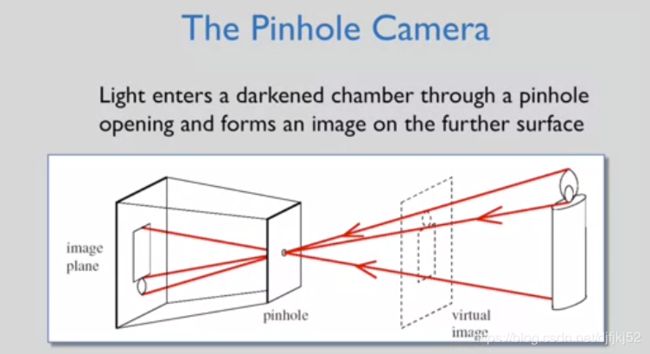
pinhole camera
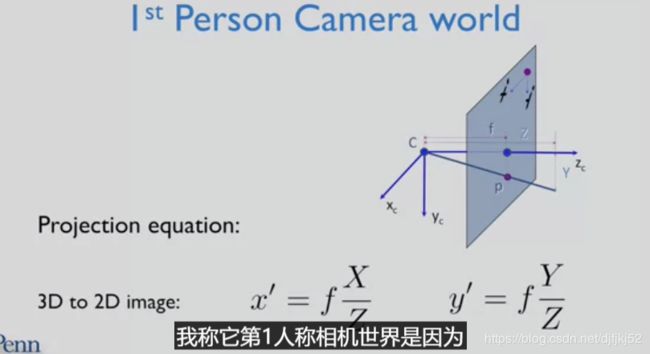
1st person camera world
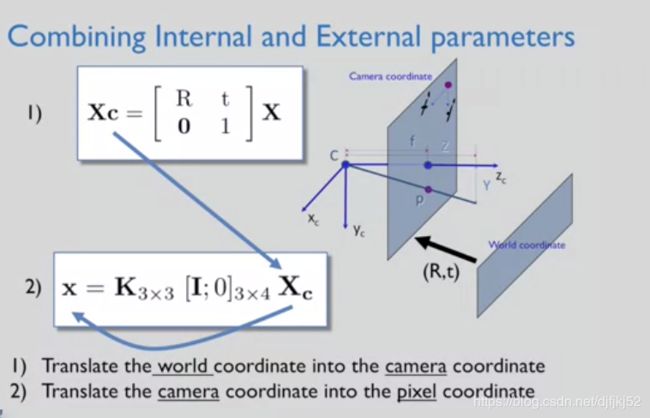
定义了第1人称相机世界的坐标系
定义第1人称相机世界 我称它第1人称相机世界是因为 ,拍照者或者说我的眼球,处在这个世界的中心 ,我在是0,0即世界的原点 所有的事物都在三维空间中以我 为中心来描述。
- 我将让x轴指向水平右边
- 然后想象y轴是竖直向下的
- 如果使用右手法则 将x叉乘y 它是指向下的 你的拇指将指向z方向 这就定义了第1人称相机世界的坐标系
而我在原点 右向是x轴 向下是y轴 向前是z轴 世界中的所有点都可以在 这个xyz坐标系表示。
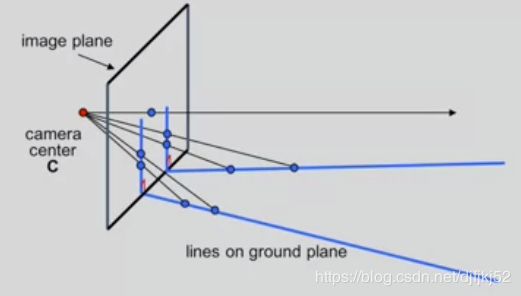
画布距离 距离恰好等于焦距(z坐标等于f )
我将把画布放在我的正前面 距离恰好等于焦距 就是说它的z坐标等于f
想象一个3D点 他们全都缩到我的相机世界中
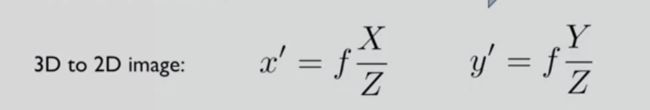
在z方向离我们远的对象 将被缩小 ,在图上将比同样大小但离我们近的对象小
进一步 如果我增大焦距 对象也会变得越来越大
另一种说法是如果我改变焦距 对象看起来就像被放大了
另一个我们能看到的事实是 像平面的大小是固定的 因此如果我通过增大焦距 使像平面远离我们 我们的视野就变小了
相反 如果你把像平面拉近 即减小焦距 我们的视野就变大了 让焦距变大 减小视野
所以我们可以从这个简单方程中得到三个 关于三维到二维投影的特性。
测量光心位置
相机第二重要参数Focal length 焦距
变化焦距的过程
改变了焦距 我们还可以看到 背景建筑和前面的物体相对大小在改变
这创造了非常有趣的视觉效果 仿佛背景的建筑 在随着焦距的变化靠近或者远离 这是一个有趣的效果 通过改变焦距创造了物体在空间中移动的效果 这与单纯放大图片是不一样的。
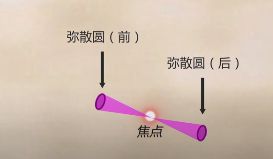
景深(DOF):超出容许弥散圆的景物清晰度下降
DOF,是指在摄影机镜头或其他成像器前沿能够取得清晰图像的成像所测定的被摄物体前后距离范围。
景深通常由物距、镜头焦距,以及镜头的光圈值所决定(相对于焦距的光圈大小)。除了在近距离时,一般来说景深是由物体的放大率以及透镜的光圈值决定。
固定光圈值时,增加放大率,不论是更靠近拍摄物或是使用长焦距的镜头,都会减少景深的距离;减少放大率时,则会增加景深。
如果固定放大率时,增加光圈值(缩小光圈)则会增加景深;减小光圈值(增大光圈)则会减少景深。
在聚焦完成后,焦点前后的范围内所呈现的清晰图像的距离,这一前一后的范围,便叫做景深。
在镜头前方(焦点的前、后)有一段一定长度的空间,当被摄物体位于这段空间内时,其在底片上的成像恰位于同一个弥散圆之间。被摄体所在的这段空间的长度,就叫景深。换言之,在这段空间内的被摄体,其呈现在底片面的影象模糊度,都在容许弥散圆的限定范围内,这段空间的长度就是景深。
关于焦点。
当人们通过一个凸透镜照射白纸时,通过前后移动透镜的位置,会在白纸上形成一个光点,甚至能引起白纸燃烧,该光点就是这个凸透镜的焦点。这个规律放到相机中来,焦点就是镜头之外的景物投射到“底片”(感光元件)的光点。这一点只要一般了解就行,平常拍摄过程中不具备操作意义。
关于调焦。
基于上面的理解,调焦的说法只对于变焦镜头才有意义,对于定焦镜头没有意义,因为它的焦距是固定不变的。对于变焦镜头来说,就是通过调整焦距从而实现对拍摄距离远、近和拍摄范围的掌控。而调焦都是靠人为理解和掌握的,因而都必须由拍摄者“亲力亲为”来控制。
关于对焦。
对焦其实是一个被动过程,对焦并不改变镜头的焦距,只是改变像距,使得拍摄对象可以清晰地成像到 “底片”(感光元件)上,通常是通过移动镜头内的透镜来实现的。
我们知道,成像必须依照1/u+1/v=1/f的定律,其中u、v和f分别代表物距、像距和焦距,一旦焦距确定(选择了定焦或完成了调焦),剩下的就是物距u和像距v关联成了一元函数关系,当我们选定了拍摄对象的主体或重点时就是确定了物距,这个时候就得调整透镜和“底照”(感光元件)的距离,确保符合成像定律,而调整透镜位置的过程就是真正的对焦。所以,对焦过程中,我们会听到“吱吱吱”的声响,就是对焦动作的听觉反馈,这个过程手动完成的就叫做“手动对焦”,相机自动完成的就叫做“自动对焦”。
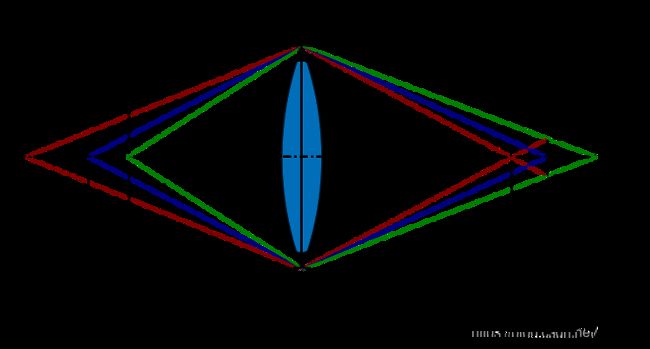
Hyperfocal distance:超焦距
超焦距或称 泛焦距离,摄影术语。是一个和焦距与光圈有关的对焦距离,当镜头以这个距离对焦时景深最大、可以从相机和对焦点之间的某处(景深前缘)起延伸到无限远(景深后缘)。
超焦距还有另一个重要的特点:如果镜头对焦在超焦距,则景深是从超焦距之半到无穷远。
如上所述,莱卡50毫米镜头在f8时的超焦距=10米。如果将镜头对焦在超焦距10米(箭头对准10米)如图四所示,则右边f8对准无穷远,左边f8对准5米(超焦距10米折半),景深从5米到无穷远。
Field of view视场角
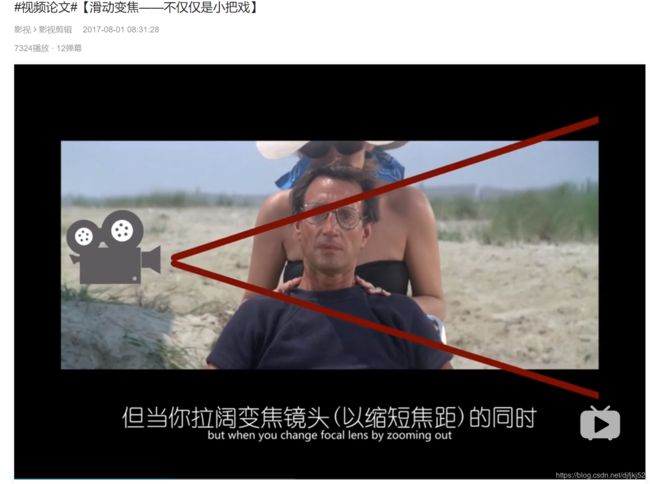
光心和焦距同时发生了改变——滑动变焦 (Dolly zoom)
滑动变焦是一种破坏正常视知觉来给人以不安感的机内特效。 滑动变焦的做法是,在转动变焦镜头改变视角的同时,把摄像机移向或者移离物体,使物体在画面中一直保持相同大小。因此,机位在远离物体的同时,镜头向前推进,或者与此相反。这样画面就会在变焦中就会产生一种连续的透视变形,最直观的特点是背景改变大小而主体不变。—— 维基百科
改变焦距 我们不仅仅在增大像平面和相机中心之间的距离,相机中心也在自行移动
一个物体的距离是依据这个物体理我的远近决定的
相机中心有两个组成部分
- 一个是物体与像平面之间的距离 这个距离不随焦距改变而变化
- 另一个组成部分是从像平面到光心的焦距 这个数量是随时在变的


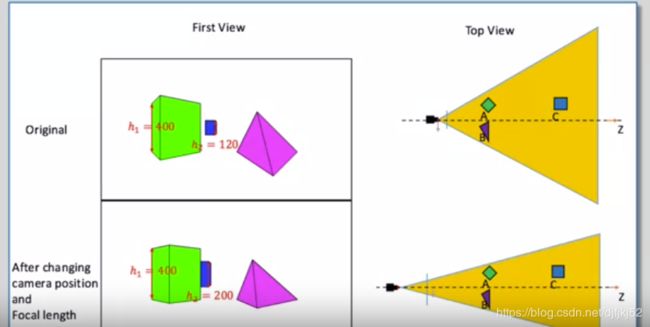
我们有一个视角和3个物体 一个绿色方块 一个蓝色方块 和右边一个粉色的角锥体
在相机所拍摄的图像中我们可以看到这样的照片 左边一个绿色的方块 中间一个蓝色的方块 右边一个粉色的东西
让我们主要分析绿色和蓝色的方块 我们看到绿色的方块在左边 在图像中高为400像素
蓝色的方块比较远 看起来更小因为蓝色的物体离得更远 蓝色物体的高度是120像素
光心和图像相交于原点 (0,0)
沿Z方向移到-4的位置 物体保持不动
我们增大焦距 在图中我们用更窄的视角表示
让我们后退一步 变化焦距后我们看到的图像变化了
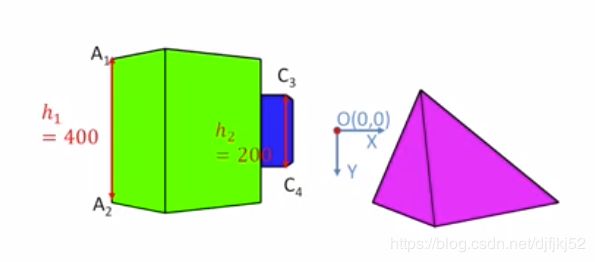
蓝色的方块看起来更大并更靠左
我们特意设计了相机的移动这样 绿色的方块仍旧是 400像素高
但是你可以看到的是 在变化焦距之后 远处的物体显得更大而不是更靠前
这张图向我们展示了这个变化
上面第一人称视角的相机在原点(0,0) 视角更宽 蓝色的方块看起来很小
这个向我们展示了这个效果,物体不动,在变的是相机本身 相机沿Z轴向后移动 同时我们不断地增加焦距 减小视角的宽度
这个过程创造了三维运动的幻觉 我们称这种效果为滑动变做或者垂直效应

可以看到,如果放大率为常数,焦距越大轴向放大率越小,焦距越小轴向放大率越大。也就是说,当在使摄像机(镜头)远离物体同时使用更长的焦距时,如果物体保持不变的放大率 M,物体会看起来更“浅”,物体之间的轴向距离更小。相反地,要使轴向放大率变大,就要将摄像机(镜头)接近物体同时使用更短的焦距。

Intrinsic Camera Parameter
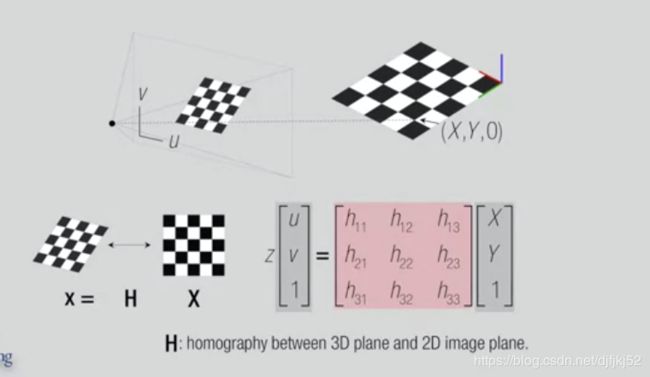
在这个三维变换空间中
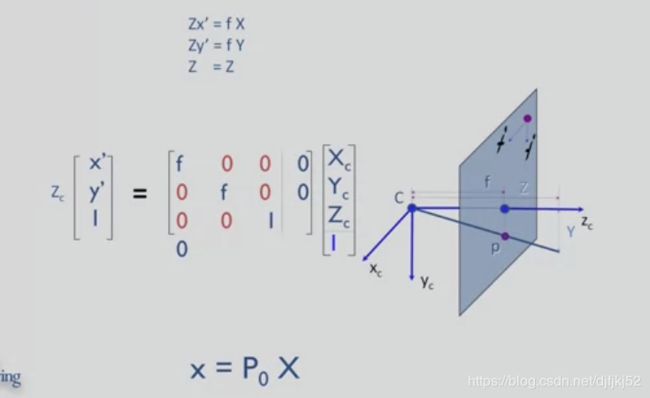
变换产生了一个 二维像空间中的三维向量
即齐次坐标 x’y’1 在像空间中 x’y’1乘以z表示一个射向3维空间的射线 并且会经过三维空间中的对应点
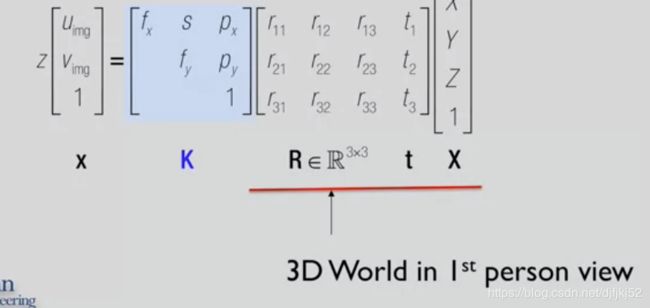
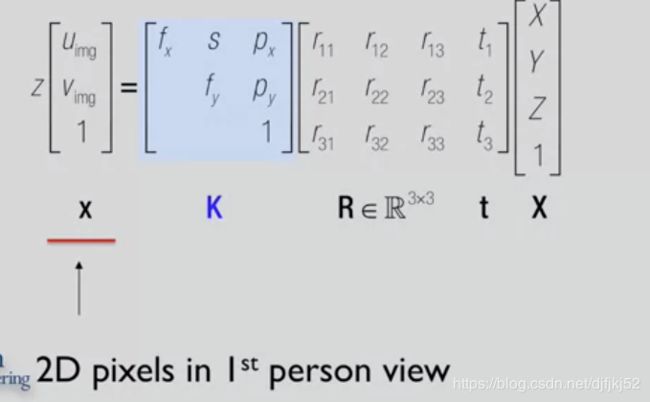
这个方程我们在后面会经常用到 它是像空间中的点
等于相机投影矩阵P乘以 X是三维空间中向量的四维齐次坐标形式。
图像在计算机 中是表示为一个矩阵的 并且矩阵的坐标原点00 通常是在图像的左上角 矩阵以第零行或第一行 第一列开始 所以00是在左上角
光学图像中我们的像平面中心 是0r0r x轴向右y轴向下 事实上 光学世界的中心 是从我们眼镜到像平面的光轴 它垂直于像平面并且与像平面 相较于一点 那一点称为主点
主点移到左上角
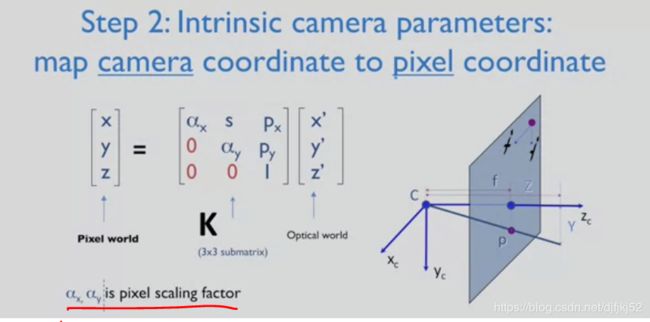
这个变换是通过一个线性变换 即将主点移到左上角 以及一个缩放因子完成的
这也可以写成矩阵形式 这个例子中是将一个二维像平面 转换到像素平面
具体的变换是一个三乘三的矩阵 或者说一个上三角矩阵 有三个部分组成
第一部分是缩放因子
与像素大小相关 怎么将毫米或厘米转换成像素
第二部分与主点相关
即光轴在哪与像平面相交 理想情况下 他应该是图像的中心
但不辛的是 由于相机或传感器的安装问题 它通常不是精确的在中心 可能往上偏移也可能往下偏移 取决于镜头是怎么装的 如果镜头偏下 光轴将在像平面中心偏下位置 与之相交

最后 由于镜头或传感器的安装问题 相机实际的像平面与理想的像平面 可能不平行 它可能有一些倾斜 这通过非对角元s描述 通过这个方程我们常做的 借助相机内参矩阵将光学射线转换为 像素射线。
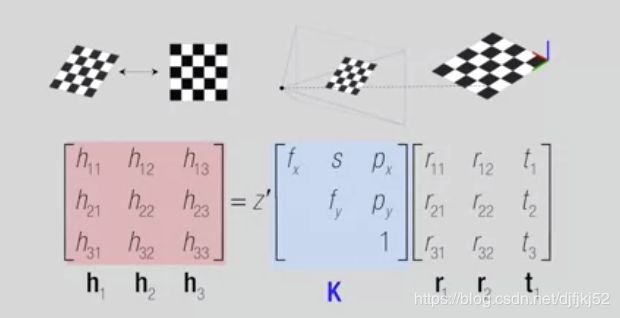
混合校准矩阵:

这个混合校准矩阵同时包含了 由焦距产生的缩放因子 以及由像素化产生的缩放因子 两者共同组成了混合校准矩阵 这个矩阵也是3乘3的 或者说是上三角的 对角元与尺度变化相关
非对角元与实际像平面与理想像平面 不平行导致的倾斜 以及主点在像平面 上的位置相关
我们称这个3乘3的矩阵为 代表一个校准矩阵
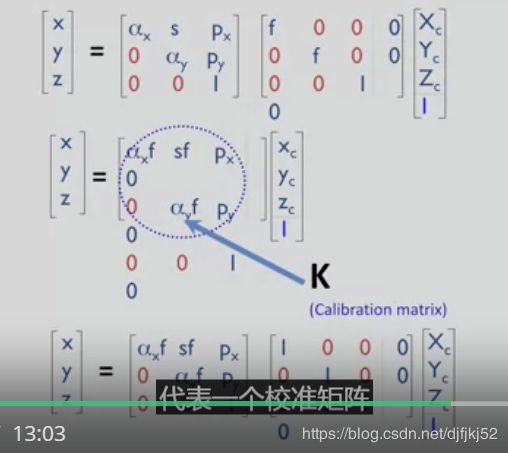
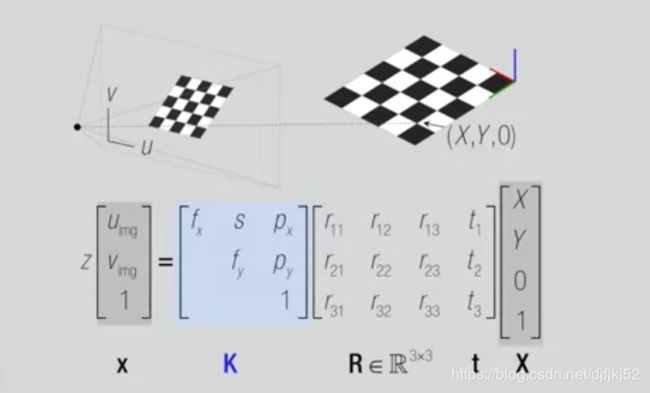
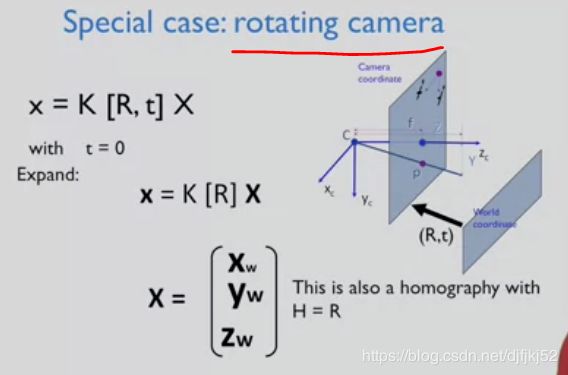
将所有东西合在一起 这是第一人称相机投影 的投影方程


再次强调第一人称相机投影矩阵是 对第一人称测量的一个三维转换矩阵 从三维世界收缩到一个二维的世界
如你所见 转换由两部分组成
- 一部分是相机校准 包含缩放因子 主点 即光轴与 像平面的交点 还有倾斜因子
- 另一部分是一个简单的单位矩阵 。(当我们换成另一个参考中心 单位矩阵将发生变化)
因为我使用第一人称来表示3维世界 我可以进一步简化方程 只用以我为参考中心的XYZ坐标 直接乘上相机校准矩阵 事实上 这将获得一个三维射线
这个射线表示成了像平面上 的齐次坐标
再次强度 相机校准矩阵包含三个因素
- 第一个是缩放因素 由焦距改变和像素尺寸决定
- 第二个与光轴与像平面交点相关 有时如果镜头安装得到 它将在像平面中心, 或者镜头因为重力发生倾斜 它可能在图像中心偏上或偏下位置
- 第三 因为光轴可能偏斜 也许因为镜头被重力拉斜了,最终图像可能与理想图像差个倾斜因子 这由s表示