深入理解计算机系统——datalab实验
实验目的:
完善bits.c里的各个函数,实现其功能,并通过btest的测试
实验说明:
实验的目标是修改bits.c的副本,以便它通过所有在btest中进行测试而不违反任何编码准则。
1、使用dlc编译器(./dlc)自动检查代码是否符合标准。
命令:unix> ./dlc bits.c
说明:如果代码没有问题,dlc会直接返回,否则,它会打印标记问题的消息。
命令:unix> ./dlc -e bits.c
说明:dlc打印每个功能使用的操作员数量。
2、使用btest进行测试
命令:unix> make btest
unix> ./btest [可选命令行参数]
说明:编译和运行btest程序(每次更改bits.c都要执行make btest重新编译)。
命令:unix> ./btest
说明:测试所有功能的正确性并打印出错误信息。
命令:unix> ./btest -g
说明:以紧凑的形式测试所有功能、错误消息。
命令:unix> ./btest -f foo
说明:测试函数foo的正确性。
命令:unix> ./btest -f foo -1 27 -2 0xf
说明:用特定参数测试函数foo是否正确。
3.助手程序
ishow和fshow程序可以查看整数和浮点表示,都需要单个十进制或十六进制数作为参数。要构建它们,执行命令:unix> make
示例用法:
unix> ./ishow 0x27
十六进制= 0x00000027,有符号= 39,无符号= 39
unix> ./ishow 27
十六进制= 0x0000001b,有符号= 27,无符号= 27
unix> ./fshow 0x15213243
浮点值3.255334057e-26
位表示形式0x15213243,符号= 0,指数= 0x2a,分数= 0x213243
标准化:+1.2593463659 X 2 ^( - 85)
linux> ./fshow 15213243
浮点值2.131829405e-38
位表示形式0x00e822bb,符号= 0,指数= 0x01,分数= 0x6822bb
标准化: +1.8135598898 X 2 ^( - 126)
实验内容及操作步骤:
完善bits.c中的函数并按照要求实现其功能,利用编译器进行测试。
一. bitAnd
题目:只能用~和|来实现位的与操作。
具体要求:
/*
- bitAnd - x&y using only ~ and |
- Example: bitAnd(6, 5) = 4
- Legal ops: ~ |
- Max ops: 8
- Rating: 1
*/
思路:这道题没什么难度,根据学习的离散数学知识,很简单可以通过摩根定律得到AB=!(!A+!B)
代码如下:
int bitAnd(int x, int y) {
return ~(~x|~y); //德摩根律,得出结果
}
二. getByte
题目:给定n (0<=n<=3),求出第n个字节是哪数字。
具体要求:
/*
- getByte - Extract byte n from word x
- Bytes numbered from 0 (LSB) to 3 (MSB)
- Examples: getByte(0x12345678,1) = 0x56
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 6
- Rating: 2
*/
思路:要想知道某个字节是哪个数字,必须将这个字节保留在最低位字节。然后每个字节是8位因此字节数n左移3(左移x位扩大2x倍)便是需要移动的位数。再与0xff进行与运算,清除高三位字节的信息并保留最低位字节的信息。
代码如下:
int getByte(int x, int n) {
int temp=x>>(n<<3); //将x左移相应字节数
return temp&0xff; //进行与运算得到最终结果
}
三. logicalShift
题目:将x按逻辑右移移动n(0<=n<=31) 位。
具体要求:
/*
- logicalShift - shift x to the right by n, using a logical shift
- Can assume that 0 <= n <= 31
- Examples: logicalShift(0x87654321,4) = 0x08765432
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 20
- Rating: 3
*/
思路:首先知道计算机的>>符号实际上是算术右移,左边会补上符号位,那么想法就是将补上的符号位都改为0.
第一种想法:
将补上的符号位与0相与,将其余各位与1相与,得到逻辑右移的结果。
利用算术右移、左移,先构造高位为1,低位为0的数:先将1左移31位,再右移n-1位,即先右移n位再左移1位,取反得到需要的结果,然后将算术右移的结果与上述结果进行与运算,得到逻辑右移的结果。
代码如下:
int logicalShift(int x, int n) {
int s = 1<<31; //将1左移31位
int temp=~((s>>n)<<1); //将s右移n-1位,并取反
return (x>>n)&temp; //temp与x算术右移n位结果相与
}
第二种想法:
是通过全1数向左移32-n位得到(其中注意为了避免出现移32位,采用了<<32+~n<<1),进行取反,然后将算术右移的结果与上述结果进行与运算,得到逻辑右移的结果。
说明:对于右移大于或等于位宽的操作,或者右移负数的操作,其结果将依赖于编译器的处理和硬件指令的处理,结果并不唯一。
代码如下:
int logicalShift(int x, int n) {
int temp=(~0)<<(32+(~n))<<1; //全为1先左移32-n-1位,再左移一位
return (x>>n)&(~temp); //将算术右移的结果与上述结果取反进行
与运算,得到逻辑右移结果。
}
四. bitCount
题目:用位运算计算出x中有多少个1
具体要求:
/*
- bitCount - returns count of number of 1’s in word
- Examples: bitCount(5) = 2, bitCount(7) = 3
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 40
- Rating: 4
*/
思路:因为要求比较严格,所以采用常规的方法会超出范围,在此想到两种思路。
第一种想法:
分治的思想
以下为每次检测4位的情况: 初始化tmp=0x1111,用来以此检测x>>i的0,8,16,24位是否为1; 利用val累加分别计算4个字节上1的个数,val的每个字节的值为对应x每个 字节上的1的个数;
最后将得到val四个字节的值相加,即x四个字节上1的个数的和,保留最低 字节的信息为最后结果
代码如下:
int bitCount(int x) {
int sum=0,mask;
mask=0x11|(0x11<<8); //mask = 0x1111
mask=mask|(mask<<16); //mask = 0x11111111
sum+=x&mask; //检测每四位中的sum的个数,分别也位于
sum的不同的8个部分中
sum+=(x>>1)&mask;
sum+=(x>>2)&mask;
sum+=(x>>3)&mask;
//4 位一组
mask=0xff|(0xff<<8); //mask = 0xffff
sum=(sum&mask)+((sum>>16)&mask);//现在sum的低16位已经比较成功地保存
了值,而且不会产生进位
mask=(0xf<<8)+0xf; //mask = 0x0f0f
sum=(sum&mask)+((sum>>4)&mask); //现在0x0f0f对应的隔两个4位也有了对应
值,为什么用0x0f0f呢,想一下,这是极端
情况时低4*4位均为1000,如果用0x00ff
必然会导致进位的混乱,于是使用0f0f保存
进位。
mask=0xff;
sum=(sum&mask)+((sum>>8)&mask);//现在结果就位于了最低几位,保存了进位,
中间加了一个0f0f使得不至于冲掉进位
使结果错误。
return sum;
}
第二种想法:
将32位划分为4个部分,每次检测8位,将检测的结果累加。
代码如下:
int bitCount(int x) {
int temp=(((0x1<<8|0x1)<<8|0x1)<<8|0x1)<<8|0x1;
int val=temp&x;
val+=temp&(x>>1);
val+=temp&(x>>2);
val+=temp&(x>>3);
val+=temp&(x>>4);
val+=temp&(x>>5);
val+=temp&(x>>6);
val+=temp&(x>>7); //8位一组
val+=(val>>16);
val+=(val>>8);
return val&0xff;
}
五. bang
题目:不能用!运算符求出!x结果
具体要求:
/*
- bang - Compute !x without using !
- Examples: bang(3) = 0, bang(0) = 1
- Legal ops: ~ & ^ | + << >>
- Max ops: 12
- Rating: 4
*/
思路:本题比较简单,只需要判断是不是0即可,然而0的特殊性,0的相反数仍然是0。
第一种想法:
考虑到只有0这个数它所有的位都为0,也就是说它的反码全为1,那么用二分法逐渐将所有的位相与最终必定为1;而其他必然会在每个过程中,因为某个位上的值为0而导致二分法求解时最终值为0。
代码如下:
int bang(int x) {
int t=~x;
t=t&(t>>16);
t=t&(t>>8);
t=t&(t>>4);
t=t&(t>>2);
t=t&(t>>1); //二分法依次进行与运算
t&=0x1;
return t;
}
第二种想法:
利用补码即其相反数,0的相反数符号位为0,而其他所有数的符号位都一定与它相反数的符号位相反,所以相或时,必定值为1,可以将其求反得0。
代码如下:
int bang(int x) {
int t=(~x)+1; //求相反数
int flag=~((x|t)>>31)&0x01; //相反数和自身相或保留符号位
return flag;
}
六. tmin
题目:返回补码整数的最小整数数值。
具体要求:
/*
- tmin - return minimum two’s complement integer
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 4
- Rating: 1
*/
思路:此题无难度。
拓展:计算机中的符号数有三种表示方法,即原码、反码和补码。 三种表示方法均有符号位和数值位两部分, 符号位都是用0表示“正”,
用1表示“负”,而数值位,三种表示方法各不相同。 在计算机系统中,数值一律用补码来表示和存储。
原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减 法也可以统一处理。
此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电 路。在补码中约定成俗,100 …000表示-2^(n-1),为最小值
代码如下:
int tmin(void) {
int ans=(1<<31);
return ans;
}
七. fitsBits
题目:只给出n个二进制位,能否表示x。
具体要求:
/*
- fitsBits - return 1 if x can be represented as an
- n-bit, two’s complement integer.
- 1 <= n <= 32
- Examples: fitsBits(5,3) = 0, fitsBits(-4,3) = 1
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 15
- Rating: 2
*/
思路:如果是一个正数或零的话,且能用相应的补码表示,则向右移动n-1位之后,此时该数的数值一定为0,如果该数是一个负数的话,如果移动n-1位后,该数的数值应该一定等于为-1,所以让x右移n-1位然后判断是否全是0或者全是1便可以。
代码如下:
int fitsBits(int x, int n) {
int temp = n+(~0); //n+0xffffffff指n-1,全1在机器中表示-1。
int tempx = x >> tmp; //x右移n-1位
int ans = (!tempx|!(tempx+1));//判断是否全为0或全为1
return ans;
}
八. divpwr2
题目:给出整数x,整数n,求[x/(2^n)],答案要接近趋向0方向。
具体要求:
/*
- divpwr2 - Compute x/(2^n), for 0 <= n <= 30
- Round toward zero
- Examples: divpwr2(15,1) = 7, divpwr2(-33,4) = -2
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 15
- Rating: 2
*/
思路:计算机中,两个int型的a和b,a/b向下取整,比如17/16,区间为(1,2),向
下取整为1,而对于负数如果-17/16区间为(-2,-1),向下取整则出现错误。
第一种想法:
正数直接右移n位则可以,负数则需要判断一下,让负数向上取整,加一个偏置值。偏置值为2n-1.
代码:
int divpwr2(int x, int n) {
int temp = (~( (x >> 31) & 0x1) )+1;//提取符号位并扩展
int q= (1<<n)+(~0); //构造偏置值
int ans = (x + (temp & q) ) >> n ; //修正后,移位实现出发
return ans;
}
第二种想法:
先获取符号位,利用符号位进行修正;然后将x的低n位保存下来,如果为负数且低n位不为0则给结果加1
代码如下:
int divpwr2(int x, int n) {
int s=!!(x>>31); //获取符号位
int t=(1<<n)+(~0);
int lowx=t&x; //上一步得到结果与x进行与运算得到x低n位
return (x>>n)+((!!lowx)&s); //判断n位是否为0,并根据符号位修正
}
九. negate
题目:给定x求-x。
具体要求:
/*
- negate - return -x
- Example: negate(1) = -1.
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 5
- Rating: 2
*/
思路:没什么难度,按位取反+1,直接返回负数。
代码如下:
int negate(int x) {
int ans=(~x)+1; //按位取反并加一
return ans;
}
十. isPositive
题目:判断x是不是正数
具体要求:
/*
- isPositive - return 1 if x > 0, return 0 otherwise
- Example: isPositive(-1) = 0.
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 8
- Rating: 3
*/
思路:反向思维,去判断不是正数的情况,负数的话符号位为1,0的话全部为0.
第一种想法:
将这两种情况进行或运算,然后再取反即最终答案。
代码如下:
int isPositive(int x) {
int temp = (x>>31) & 0x1; //取符号位
int ans = !( temp | !x ); //判断是否为负数或0
return ans;
}
第二种想法:
x的无符号值必定或者为0,或者不为0,这里只可能是为负数(!flag=0,!x=0),或者为0(!flag=1,!x=1),为正数时(!flag=1,!x=0),所以可以采用异或。
代码如下:
int isPositive(int x) {
int flag=(x>>31);
flag&=0x1; //取符号位
return (!flag)^(!x); //使用异或进行判断
}
十一. isLessOrEqual
题目:用位运算判定x<=y,如果是就返回1,如果不是就返回0。
具体要求:
/*
- isLessOrEqual - if x <= y then return 1, else return 0
- Example: isLessOrEqual(4,5) = 1.
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 24
- Rating: 3
*/
思路:想判断x<=y,肯定要去判断y-x是否位负数,但是又考虑到最大的整数减去最小的负数会溢出导致出现错误的结果,那么想办法解决这个问题。
- 当相同符号时,直接相减判断是否为负数即可。
- 当前者为正,后者为负时,直接返回0,前者为负后者为正时返回1。
代码如下:
int isLessOrEqual(int x, int y) {
int signx = (x >> 31) &0x1; //取x的符号位
int signy = (y >> 31) &0x1; //取y的符号位
int isSameSign=! (signx ^ signy) ;// 对符号位异或取反,判断是否相同
int p=! ( ( (~x)+1+y ) >> 31); //计算y-x,并取结果的符号位
//p为1表示x<=y(x,y同号)
return ( isSameSign & p ) | ( ( !isSameSign ) & signx));
}
十二. ilog2
题目:求整数的log(x)。
具体要求:
/*
- ilog2 - return floor(log base 2 of x), where x > 0
- Example: ilog2(16) = 4
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 90
- Rating: 4
*/
思路:该题和之前那道求1的个数类似,也需要采用二分的思想,先判断第一个1在前16位还是后16位,记录下来,再判断再前8位还是后8位,一直做到判断在前1位还是后1位,便是最终答案。公式log(x)=16a+8b+4c+2d+e。那么count=abcde。因为x长32位,首先我们先将x>>16,判断高16位是不是还>0,如果>0,!(x>>16)就是0,我们要将他转换到a的位置就是将!!(x>>16)再次取非是1,然后<<4,到a的位置,就说明这个数大于16,1肯定在高16位处,然后在接着将高位折半到8位,就是>>8+16,看看高8位是不是也是>0。依次进行下去直到判断前一位还是后一位……(此处应该为无符号数)
代码如下:
int ilog2(int x) {
int count = 0;
count = (!!(x>>16)) << 4; //判断前十六位有没有值,决定起点
count =count+((!!(x>>(8 + count)))<<3);//判断剩下十六位的前八位
count =count+((!!(x>>(4 + count)))<<2);//判断剩下八位的前四位
count =count+((!!(x>>(2 + count)))<<1); //判断剩下四位的前两位
count =count+((!!(x>>(1 + count)))<<0); //判断剩下两位的前一位
return count;
}
十三. float_neg
题目:就是返回输入uf的负数形式-uf。如果uf是NAN形式就直接返回参数。
具体要求:
/*
- float_neg - Return bit-level equivalent of expression -f for
- floating point argument f.
- Both the argument and result are passed as unsigned int’s, but
- they are to be interpreted as the bit-level representations of
- single-precision floating point values.
- When argument is NaN, return argument.
- Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
- Max ops: 10
- Rating: 2
*/
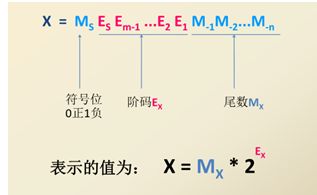
思路:浮点数是由s(符号1位)E(阶码8位)M(尾数23位)(-1)^s * M * 2^E组成的浮点数,当E是0xFF时,要么这个数是inf(无穷)或NAN。
- inf特殊在M就是全0 计算-uf(不考虑函数里参数和返回值类型,uf解释为浮点数),符号位取反可利用异或 (符号位的求反)
- 当x=NaN时,阶码全为1,小数位不为0,返回NaN; (非数值数的特殊情况)
- 当x=!NaN时,直接将符号位取反返回-x即可;
(因为阶码用移码表示,不 须求反,尾数也不须求反,因为并非像负数那样用补码表示)
第一种想法:
先把uf<<1忽略了s,就看看0xFF000000在uf<<1的位置是不是也是
0xFF000000,如果是再判断一下uf是不是就等于0xFF000000就代表他原先就是个inf数,如果不等于0xFF000000就代表他原先就是个NAN数。然后如果是NAN数的话直接返回原值便可以了。
代码如下:
unsigned float_neg(unsigned uf) {
unsigned s=0x80000000;
unsigned no=0xFF000000;
unsigned tmp = uf<<1;
if( (no&tmp ) == no) // 判断E是否全为一
{
if(tmp != no) return uf; //判断是否为inf,不是返回uf
}
return uf^s;
}
第二种想法:
判断是否,阶码并非全为1,或着尾数为0 ,如果是,则直接符号位取反,返回,否则为NAN,直接返回。
代码如下:
unsigned float_neg(unsigned uf) {
if((((uf>>23)&0xff)^0xff)||!(uf&((1<<23)-1)))//阶码并非全为1,或着尾数为0,通过将阶码按位取反,这里其实可以用~,当然也可用全1的异或操作
uf^=(1<<31);
//阶码不全为1或者尾数为0
//尾数为0,而阶码不全1,当然需要将其变为负数
//尾数为0,而阶码全1,指的是无穷大,也应该需要改变符号位。
//只有当阶码全1且而且尾数不为0则返回NaN. 除去非数值数就好了。
return uf;
}
十四. float_neg
题目:将int型的x转为float型的x。
具体要求:
/*
- float_i2f - Return bit-level equivalent of expression (float) x
- Result is returned as unsigned int, but
- it is to be interpreted as the bit-level representation of a
- single-precision floating point values.
- Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
- Max ops: 30
- Rating: 4
*/
思路:先判断是否为0或者-231;然后判断是否是负数,是负数的话先转化为正数,因为float正负数的区别只是符号位不一样。再然后将x右移确定阶码的大小。确定了阶码和符号位以后再去考虑尾码,将x左移到第一个1,然后再右移8,与0x007fffff进行与运算这样的结果便是除去隐藏位的前23位。让x与0xff相与,这是23位之后舍去的8位数据,利用浮点数的偶数取余原则,当大于0.5则进1,当等于0.5且第23位为1的时候也进1,否则不进位。如果进位后使尾数溢出,那么让阶码加1,尾数将溢出位清0.
代码如下:
unsigned float_i2f(int x) {
unsigned s=x&(1<<31); //保存符号位
int i=30;
int exp=(x>>31)?158:0; //判断x是否为0或-231,对exp进行设置
int frac=0; //尾数初始化为0,之后进行更新
int delta; //用来保存精度
int frac_mask=(1<<23)-1; //frac_mask低23位全1,高9位全0
if(x<<1) //如果x不为0也不为-231 (000...000指0,而100...000指-2^31)
{
if(x<0)
x=-x; //正数变为负数,因为要换成原码实现,由于可以直接这样转换,就转换成为其原码,而不用我们之前的表示法
while(!((x>>i)&1)) //要看其最高位的位置,一开始向右移30位,而后依次减小,这个30位就是从符号位的下一位起移至最右边如果有一个时刻这一位变成了1,那么也就是说,这个i指的就是最高位
i--;
exp=i+127; //原码=E+Bias,Bias=127
x=x<<(31-i); //舍弃前面的0,这时可以看作是尾数,找到第1个1的位置
frac=frac_mask&(x>>8); //frac取尾数(取x的高23位),注意这里前面还有一个1
x=x&0xff; //保留x的低8位
delta=x>128||((x==128)&&(frac&1));
//处理精度,四舍五入,判断是否需要进位,就是我们在上面判断的,而且需要用到一系列逻辑判断符进行判断,遵循向偶数舍入的原则,即||后面的情况
frac+=delta;
if(frac>>23) //如果尾数加上进位溢出
{
frac&=frac_mask; //取尾数的后23位
exp+=1; //产生进位
}
} //如果为0或-231则,首先不改变符号位,而后由于我们之前帮阶码赋了值(如果为负数,阶码值为31;如果为0,阶码值为-127全零),而尾数第一位被省略,所以能产生正确结果。
return s|(exp<<23)|frac;
}
十五. float_twice
题目:就是将浮点数乘以2倍。
具体要求:
/*
- float_twice - Return bit-level equivalent of expression 2*f for
- floating point argument f.
- Both the argument and result are passed as unsigned int’s, but
- they are to be interpreted as the bit-level representation of
- single-precision floating point values.
- When argument is NaN, return argument
- Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
- Max ops: 30
- Rating: 4
*/
思路: 浮点数的运算要考虑三部分:符号,阶码和尾数计算uf*2,分两种情况:
(1)阶码部分为0,只需对尾数部分左移一位;(包含尾数移至阶码位的情况这 里要注意
(2)阶码部分不为0,则将阶码加1;(因为不可以将尾数部分移到阶码部分)
- 取符号位方法:s=uf&(1<<31);
- 取8位阶码方法:exp=(uf>>23)&0xff
- 取尾数:frac=uf&((1<<23)-1); *
- 判断uf是否为NaN,如果是,不做处理,最后返回NaN;
将符号、阶码、尾数三部分整合到返回值;即:ret=s|(exp<<23)|frac
第一种想法:
三个部分进行运算,直接拼接
代码如下:
unsigned float_twice(unsigned uf) {
unsigned s=uf&(1<<31); //取符号位
int exp=(uf>>23)&0xff; //取阶码
int frac=uf&((1<<23)-1); //取尾数
if((exp!=0xff)) //如果阶码值为255,且尾数部分不为0,则该数为非数值数
{
if(!exp) //如果阶码为0,则将尾数左移一位,在这种情况下如果尾数的最高位为1,则也可以移到阶码处,从而使得阶码值价一,这样就进入了规范化数的表示范围
{
if(frac&0x00400000)
exp++; //尾数最高位为1,阶码+1
frac = (frac << 1) & 0x007fffff;
//否则,尾数左移
}
else //如果阶码不为0
{
exp++;
if(exp==255)
frac=0; //如果所得阶码为255,将尾数设置为0,表示无穷大
}
} //省略else情况,即uf为NaN和无穷大数,在这种情况下,阶码已经全1,无论如何都不能改变了。
return s|(exp<<23)|frac;
}
第二种想法:
按位操作。
代码如下:
unsigned float_twice(unsigned uf) {
unsigned f=uf;
if ((f & 0x7F800000) == 0){ //判断阶码是否全为0
f = ((f & 0x007FFFFF)<<1) | (0x80000000 & f);
} //保留符号位,并将尾数左移,注意分两种情况:(1)尾数首位为1,移至阶码处,值确实变为原来的两倍(2)尾数首位不为1,则更加可以放心地移动了
else if ((f & 0x7F800000) != 0x7F800000){
//判断阶码是否不全为1
f =f+0x00800000; //阶码+1
}
return f;
}
相关知识点:
1.常用逻辑运算符
- a|=b 等效于 a=a|b 按位或并赋值。
- a&=b 等效于 a=a&b 按位与并赋值。
- a^=b 等效于 a=a^b 按位异或并赋值。
- a!=b 逻辑判断,不等于,当ab不等时为真。
- && 逻辑与,均为真时结果为真 || 逻辑或,均为假时结果为假。
- !a 逻辑非,单目,a为真时结果为假,否则结果为真。
- | 按位或
- ^ 按位异或
- & 按位与
- ~ 按位取反
2.左移32位,根据编译器不同,结果不同,所以在实际的运算过程中要避免左移32位。
左移就是把一个数的所有位都向左移动若干位,在C中用<<运算符.例如:
int i = 1;
i = i << 2; //把i里的值左移2位
也就是说,1的2进制是000…0001(这里1前面0的个数和int的位数有关,32位机器,gcc里有31个0),左移2位之后变成 000…0100,也就是10进制的4,所以说左移1位相当于乘以2,那么左移n位就是乘以2的n次方了(有符号数不完全适用,因为左移有可能导致符号变化,下面解释原因)
需要注意的一个问题是int类型最左端的符号位和移位移出去的情况.我们知道,int是有符号的整形数,最左端的1位是符号位,即0正1负,那么移位的时候就会出现溢出,例如:
int i = 0x40000000; //16进制的40000000,为2进制的01000000…0000
i = i << 1;
那么,i在左移1位之后就会变成0x80000000,也就是2进制的100000…0000,符号位被置1,其他位全是0,变成了int类型所能表示的最小值,32位的int这个值是-2147483648,溢出.如果再接着把i左移1位会出现什么情况呢?在C语言中采用了丢弃最高位的处理方法,丢弃了1之后,i的值变成了0.
左移里一个比较特殊的情况是当左移的位数超过该数值类型的最大位数时,编译器会用左移的位数去模类型的最大位数,然后按余数进行移位,如:
int i = 1, j = 0x80000000; //设int为32位
i = i << 33; // 33 % 32 = 1左移1位,i变成2
j = j << 33; // 33 % 32 = 1 左移1位,j变成0,最高位被丢弃