数据结构与算法(五)(排序算法)
冒泡排序
1.思路分析:假设有一个数组3,-1,10,9,-2
第一次排序:
-1,3,10,9,-2(比较3,-1,换位)
-1,3,10,9,-2(比较3,10)
-1,3,9,10,-2(比较10,9,换位)
-1,3,9,-2,10(比较10,-2,换位)第一次排序结束10不再变化
第二次排序:
-1,3,9,-2,10(比较-1,3)
-1,3,9,-2,10(比较3,9)
-1,3,-2,9,10(比较9,-2,换位)第二次排序结束9不再变化
第三次排序:
-1,3,-2,9,10(比较-1,3)
-1,-2,3,9,10(比较3,-2,换位)第三次排序结束3不再变化
第四次排序:
-2,-1,3,9,10(比较-1,-2,换位)第四次排序结束-1不再变化
2.思路总结
总共进行length-1次大排序,每一次排序的次数在减少
3.代码实现
package sorting;
import java.lang.reflect.Array;
import java.util.Arrays;
public class Bubble {
public static void main(String[] args) {
int[] arrays = {3,-1,10,9,-2};
//辅助换位变量
int num = 0;
boolean flag = false;
for(int i=0;i<arrays.length-1;i++){
for(int j =0;j<arrays.length-1-i;j++){
if(arrays[j]>arrays[j+1]){
flag = true;
num = arrays[j+1];
arrays[j+1] = arrays[j];
arrays[j] = num;
}
}
System.out.println(Arrays.toString(arrays));
//此处为优化,如果没有换位发生就直接退出,证明已经排好序
if(!flag){
break;
}else {
flag = false;
}
}
}
}
选择排序
1.思路分析
假定有数组:101,34,119,1
第一次排序:选择4个数字中最小的1与101交换 1,34,119,101
第二次排序:选择3个数字中最小的34和34交换 1,34,119,101
第三次排序:选择2个数字中最小的101和119交换 1,34,101,119
2.思路总结
总共需要进行array.length-1次排序,每次排序里面又是一次循环,目的是找到最小的数字,先让当前数字为最小数字,再和后面的比较,最后完成换位
3.代码实现
package sorting;
import java.lang.reflect.Array;
import java.util.Arrays;
public class Selection {
public static void main(String[] args) {
int[] arrays = {101,34,119,1};
//记录最小值的位数
int num = 0;
//记录最小值
int min = 0;
for(int i=0;i<arrays.length-1;i++){
//假设最小值是第一位
min = arrays[i];
boolean flag = false;
for(int j=0+i;j<arrays.length-1;j++){
if(min>arrays[j+1]){
flag = true;
min = arrays[j+1];
num = j+1;
}
}
//换位
if(flag){
arrays[num] = arrays[i];
arrays[i] = min;
}
System.out.println(Arrays.toString(arrays));
}
}
}
插入排序
1.思路分析
假定有数组101,34,2,1
第一次排序,先将101放入有序表中,剩下的元素则在无序表中,将34拿出,放入有序表(比较34和101的大小,如果101大,将101后移一位,将34放到101的位置),此时有序表为34,101
第二次排序,此时有序表中有34,101,将2拿出,放入有序表(2先和101比较,将101后移,2再和34比较,将34后移,2放在34的位置上),此时有序表为2,34,101
第三次排序,同上两次排序
2.思路总结
总共需要length-1次大排序,每次小排序,是将当前数字与有序表中数字做对比,大的后移,最终找到当前数字的位置
3.代码实现
package sorting;
import java.lang.reflect.Array;
import java.util.Arrays;
public class Insert {
public static void main(String[] args) {
int[] array = {101,34,2,1};
//当前要插入的数值
int arrVal = 0;
//要比较的坐标
int arr = 0;
for(int i=1;i<array.length;i++){
arrVal = array[i];
arr = i-1;
while(arr>=0 && arrVal<array[arr]){
array[arr+1] = array[arr];
arr--;
}
array[arr+1] = arrVal;
System.out.println(Arrays.toString(array));
}
}
}
希尔排序
1.与插入排序相比的优势,比如有数组2,3,4,5,1,此时如果使用插入排序,后移的次数比较多,浪费时间,此时应使用希尔排序
2.算法分析,假如有数组,8,9,1,7,2,3,5,4,6,0,该数组总共10个数字
第一次排序,10/2 = 5,将数组分为5组,{8,3},{9,5},{1,4},{7,6},{2,0}
将这5组分别排序,结果为3,5,1,6,0,8,9,4,7,2
第二次排序,5/2=2,将数组分为2组{3,1,0,9,7},{5,6,8,4,2},将这两组分别排序,结果为0,2,1,4,3,5,7,6,9,8
第三次排序,2/2=1,此时将数组分为1组,进行最后一次排序
3.在分组过后的排序时,有两种方法,换位法(好理解,速度慢),移位法(速度快)
4.换位法代码实现
package sorting;
import java.util.Arrays;
public class Shell {
public static void main(String[] args) {
int[] arr = {8,9,1,7,2,3,5,4,6,0};
for(int gap =arr.length/2;gap>0;gap /= 2){
for(int i=gap;i<arr.length;i++){
for(int j=i-gap;j>=0;j-=gap){
if(arr[j]>arr[j+gap]){
//此处为换位操作
int temp = arr[j];
arr[j] = arr[j+gap];
arr[j+gap] = temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
}
}
5.移位法代码实现
package sorting;
import java.util.Arrays;
public class Shell {
public static void main(String[] args) {
int[] arr = {8,9,1,7,2,3,5,4,6,0};
int arrVal = 0;
int ar = 0;
for(int gap = arr.length/2;gap>0;gap/=2){
for(int i=gap;i<arr.length;i++){
//要插入的数字
arrVal = arr[i];
//坐标
ar = i-gap;
while(ar>=0 && arrVal<arr[ar]){
arr[ar+gap] = arr[ar];
ar -= gap;
}
arr[ar+gap] = arrVal;
}
}
System.out.println(Arrays.toString(arr));
}
}
快速排序
1.算法简介:快速排序是对冒泡排序的一种优化,将一组数字按照其中某一个数字分为两组,一组大于该数字,一组小于该数字,递归以上行为直到变为有序
2.算法分析,假如有数组-9,78,0,23,-567,70,此时我们取数字0为基准点,让比0小的数字放在0的左面,让比0大的数字放在0的右面,此时排序结果为-9,-567,0,23,78,70,再让-9,-567和23,78,70重复此过程,最后得到有序数组
3.代码实现
package sorting;
import java.util.Arrays;
public class Quick {
public static void main(String[] args) {
int[] arr = {-9,78,0,23,-567,70};
quickSort(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr,int left,int right){
int l = left;
int r = right;
//取基准点
int pivot = arr[(left+right)/2];
//用于辅助交换
int temp = 0;
while(l<r){
while(arr[l]<pivot){
l+=1;
}
while(arr[r]>pivot){
r-=1;
}
if(l>=r){
break;
}
temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
//此处代码避免死循环
if(arr[l] == pivot){
r-=1;
}
if(arr[r] == pivot){
l+=1;
}
}
//此处代码避免栈溢出
if(l==r){
l+=1;
r-=1;
}
if(left<r){
quickSort(arr,left,r);
}
if(right>l){
quickSort(arr,l,right);
}
}
}
归并排序
1.算法简介:该算法采用经典的分治思想,把一组数字分成多组进行排序然后递归求解
2.算法分析:

总共需要进行7次排序,8个数字7次排序,80个数字79次排序,时间复杂度比较低
而其中治的过程比较重要:
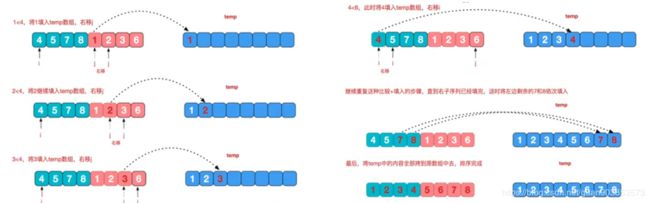
3.代码实现
package sorting;
import java.util.Arrays;
public class Merget {
public static void main(String[] args) {
int[] arr = {8,4,5,7,1,3,6,2};
int[] temp = new int[arr.length];
mergetSort(arr,0,7,temp);
System.out.println(Arrays.toString(arr));
}
//分的过程
public static void mergetSort(int[] arr,int left,int right,int[] temp){
if(left<right){
int mid = (left+right)/2;
mergetSort(arr,left,mid,temp);
mergetSort(arr,mid+1,right,temp);
merget(arr,left,mid,right,temp);
}
}
//治的过程
public static void merget(int[] arr,int left,int mid,int right,int[] temp){
int i = left;
int j = mid+1;
int t= 0;
//将左右两侧的有序数组按照规则填充进入temp中
while(i<=mid && j<=right){
if(arr[i]<arr[j]){
temp[t] = arr[i];
t++;
i++;
}else{
temp[t] = arr[j];
t++;
j++;
}
}
//将剩余的数字填充进去
while(i<=mid){
temp[t] = arr[i];
i++;
t++;
}
while(j<=right){
temp[t] = arr[j];
j++;
t++;
}
//将temp填充进入arr中,注意不是每一次都是完全填充
t = 0;
int tempLeft = left;
while(tempLeft<=right){
arr[tempLeft] = temp[t];
t++;
tempLeft++;
}
}
}
基数排序
1.算法简介:基数排序是桶排序的扩展,基数排序属于稳定性的排序,比如10,0(第一个0),1,0(第二个0),排序过后0(第一个0),0(第二个0),1,10,此时第一个0依旧在第二个0前面,这就叫做稳定性排序,基数排序是经典的空间换时间的排序算法
2.算法分析



3.算法总结:先从数组中取出最大值,之后看最大值为几位数,就进行几次排序,从个位开始排序,放入桶中,再取出,从十位开始排序,放入桶中,再取出。。。
4.代码实现
package sorting;
import java.util.Arrays;
public class Radix {
public static void main(String[] args) {
int[] arr = {53,3,542,748,14,214};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void radixSort(int[] arr ){
//此处为桶
int[][] buckets = new int[10][arr.length];
//此处记载那个桶中有数字,比如bucketMark[0]=1,就是第一个桶中有一个数字
int[] bucketMark = new int[10];
//此处找到最大数字,并且得到最大数字得位数
int max = arr[0];
for(int i=1;i<arr.length;i++){
if(arr[i]>max){
max = arr[i];
}
}
int length = (max+"").length();
for(int m =0,k=1;m<length;m++,k*=10){
//将数字按照个位,十位,百位放入桶中
for(int i=0;i<arr.length;i++){
int number = arr[i]/k%10;
buckets[number][bucketMark[number]] = arr[i];
bucketMark[number]++;
}
//取出数字放入数组
int index = 0;
for(int i=0;i<bucketMark.length;i++){
if(bucketMark[i]!=0){
for(int j=0;j<bucketMark[i];j++){
arr[index] = buckets[i][j];
index++;
}
}
bucketMark[i] = 0;
}
}
}
}
堆排序
1.基本概念介绍:
堆排序是以树(完全二叉树)结构为基础的一种排序算法,堆排序是选择排序
大顶堆:每个节点的值都大于或者等于其左右子节点的值(适合升序排列)
小顶堆:每个节点的值都小于或者等于其左右子节点的值(适合降序排列)
2.思路分析
将无序序列构建成一个堆,根据升序降序选择大顶堆或者小顶堆
将堆顶元素与末尾元素交换,将最大的元素沉到数组末端
重新调整结构,使其满足堆的定义,然后继续此过程
3.代码实现
package sorting;
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] arr = {4,6,8,5,9};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
//排序方法
public static void heapSort(int[] arr){
int temp ;
//第一次排序
for(int i=arr.length/2-1;i>=0;i--){
adjustHeap(arr,i,arr.length);
}
//开始换位并接着排序
for(int j=arr.length-1;j>0;j--){
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr,0,j);
}
}
//将数组变成大顶堆
public static void adjustHeap(int[] arr,int i,int length){
//帮当前的数值存起来
int temp = arr[i];
//循环找i的左子节点
for(int k = i*2+1;k < length;k = k*2+1){
//比较左子节点和右子节点那个大
if(k+1<length && arr[k]<arr[k+1]){
k++;
}
//如果子节点大就换位
if(arr[k]>temp){
arr[i] = arr[k];
i=k;
}else{
break;
}
}
arr[i] = temp;
}
}
排序算法时间复杂度比较
| 排序算法 | 时间复杂度 | 稳定性 |
|---|---|---|
| 冒泡排序 | O(n的平方) | 稳定 |
| 选择排序 | O(n的平方) | 不稳定 |
| 插入排序 | O(n的平方) | 稳定 |
| 希尔排序 | O(nlogn) | 不稳定 |
| 归并排序 | O(nlogn) | 稳定 |
| 快速排序 | O(nlogn) | 不稳定 |
| 堆排序 | O(nlogn) | 不稳定 |
| 计数排序 | O(n+k) | 稳定 |
| 桶排序 | O(n+k) | 稳定 |
| 基数排序 | O(n+k) | 稳定 |
k:表示桶的数量
n:表示待排序数字数量