计算机图形学（二）输出图元_11_OpenGL多边形填充区函数（上）

OpenGL多边形填充区函数（上）

        描述填充多边形的OpenGL过程与描述点和折线类似，但有一个例外。函数glVertex用来输入 多边形的一个顶点坐标，而完整的多边形用从glBegin到glEnd之间的一组顶点来描述。但有另外 一个函数可以用来显示具有完全不同格式的矩形。
        默认时多边形内部显示为单色，由当前颜色设定确定其颜色。作为选项(下面的内容中叙述)， 可以用图案填充多边形且显示多边形的边作为内部填充的边界。函数glBegin中指定多边形填充区 的变量可使用6个不同的符号常量。这6个基本常量可用来显示单一填充多边形、一组不相连的填 充多边形或一组相连的填充多边形。
       OpenGL中的填充区必须指定为凸多边形。因此，一个填充多边形的顶点集中至少包含三个顶 点，其中无相交边，多边形所有内角均小于180度。单个多边形填充区只用一个顶点集描述，其内部 不能包含图3.54所示的洞。那样的图形可用两个重叠的多边形来描述。
    我们描述的每一个多边形有两个面:后向面和前向面。在OpenGL中，可以为每个面分别设定 填充颜色和其他属性，且在二维和三维观察子程序中要求有后向/前向标志。因此，多边形按从“外 部”观察它时的逆时针方向描述。这标识了该多边形的前向面。

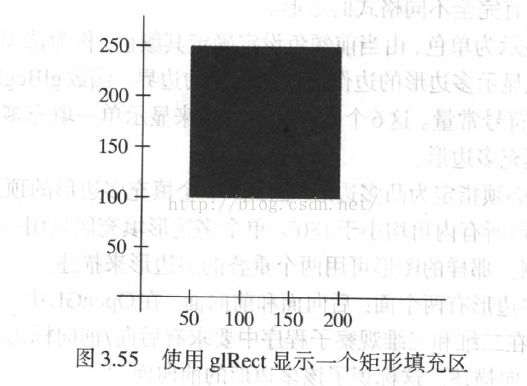
       因为图形显示中经常包含有矩形的填充区，OpenGL提供了一个特殊的矩形函数， 直接在xy平面中描述顶点。在有些OpenGL的实现中，下面的函数比用g1Vertex描述的填充区有更高的效率：

glRect* (x1, y1, x2, y2);

       该矩形的一个角位于坐标位置(x1,y1)处，而与其相对的一角位于坐标位置(x2,y2)处。glRect的后缀 码指出坐标数据类型及是否用数组元素来表示坐标。这些编码是i(整数)、s(短整数)、f(浮点 数)、d(双倍长浮点数)和v(向量)。矩形的边平行于xy坐标轴。作为一个例子，下面的语句定 义了图3.55中给出的正方形:

glRecti (200, 100,50, 250);

       如果将坐标值放在数组中，可用下列语句生成同样的正方形：

int vertex1 [] = { 200, 1000};
int vertex2 [] = { 50, 250};
glRectv (vertex1, vertex2);

       利用函数glRect生成矩形时，多边形的边按顶点序列(x1,y1)、(x2,y1)、(x2,y2)、(x1,y2)来形成， 后返回到第一顶点(x1,yl)。在该例子中，我们生成了顺时针次序的顶点集。在许多二维应用中，前 向面和后向面的确定是不重要的。但如果确实要将不同的特性赋给矩形的前向面和后向面，那就应 该将本例中的两个顶点次序倒过来从而得到逆时针的顶点次序。第4章将讨论另一种可以颠倒前向
面和后向面描述的方法。

       另外六个OpenGL多边形填充图元中的每一个都用glBegin函数中的符号常量及一组glVertex 命令描述。使用OpenGL图元常量GL_POLYGON可以显示图3.56(a)那样的单个多边形。在该例子 中，我们假定有六个顶点，标号p1到p6，描述一个逆时针次序的两维多边形顶点位置。每一点用 一个数组(x,y)坐标值表示。

glBenin (GL_POLYGON);
 glVertex2iv (p1);
 glVertex2iv (p2);
 glVertex2iv (p3);
 glVertex2iv (p4);
 glVertex2iv (p5);
 glVertex2iv (p6);
glEnd();

一个多边形的顶点集至少包含三个顶点，否则什么也不显示。
 如果改变前一例子中顶点集的次序并将图元常量改变成GL_TRIANGLES，就获得图3.56(b)所示的两个分开的三角形填充区。

glBenin (GL_TRIANGLES);
 glVertex2iv (p1);
 glVertex2iv (p2);
 glVertex2iv (p3);
 glVertex2iv (p4);
 glVertex2iv (p5);
 glVertex2iv (p6);
glEnd();

     此时，前面三个坐标点定义一个三角形的顶点，后面三点定义下一个三角形，依次类推。对于每一个三角形填充区，我们指定逆时针次序的顶点位置。除非重复使用某些顶点，否则该图元常量仅显示不相连的三角形。如果顶点数小于3,则什么也不显示。而如果指定的顶点数不是3的倍数，则最后一个或两个顶点没有用。
    再次改变顶点集次序并将图元常量改为GL_TRIANGLE_STRIP，可显示图3.56(c)所示的一组连接的三角形。

glBenin (GL_TRIANGLE_STRIP);
 glVertex2iv (p1);
 glVertex2iv (p2);
 glVertex2iv (p6);
 glVertex2iv (p3);
 glVertex2iv (p5);
 glVertex2iv (p4);
glEnd();

        假定在N个顶点的集合中没有重复的坐标位置，可获得N-2个三角形的带。很清楚，必须有N >= 3，否则什么也不显示。在该例子中， N=6，得到4个三角形。每一后继三角形共享前面定义的三角形的一条边，因此顶点次序的设定必须保证显示的一致性。一个三角形在前面两个顶点的基础上再加一个顶点来定义。 因此，最前面三个顶点必须按从前面(外部)观察三角形表面时的逆时针次序列出。随后，顶点表中用于另外三个三角形的三个顶点安排成顺时针次序。这通过按次序n=1,n=2....n = N-2处理顶点集中的位置n，并按n是否为奇数或偶数确定相应的三顶点集次序来实现。如果n是奇数，三角形顶点的多边形列表次序是n 、n+1、 n+2。如果n是偶数，则三角形顶点次序为。n+l、n、n+2。在前面的例子中，第一个三角形(n=1)的顶点次序为(p1, p2, p6)。第二个三角形(n = 2)的顶点次序为(p6, p2, p3)。第三个三角形(n=3)为(p6, p3, p5)。多边形表中第四个三角形(n=4)的顶点次序为(p5， p3, p4)。
       生成一组相连三角形的另一种方法是使用图3.56(d)所示的“扇形”方法，其中有一个顶点被所有的三角形共享。使用图元常量GL_TRIANGLE_FAN和六个顶点的原来次序可以获得这样的设置:

glBenin (GL_TRIANGLE_FAN);
 glVertex2iv (p1);
 glVertex2iv (p2);
 glVertex2iv (p3);
 glVertex2iv (p4);
 glVertex2iv (p5);
 glVertex2iv (p6);
glEnd();

      N个顶点可获得N-2个三角形，不需要重复使用任何顶点，但必须至少列出三个顶点。另外，必须合适地描述顶点次序，以便正确定义每一个三角形的前向面和后向面。第一个列出的顶点(此时为pl )是扇形中每一三角形共享的顶点。如果再按n=1,n=2,...,n=N-2来计算多边形和坐标位置，则多边形表中第n个三角形的顶点次序为1, n+1 , n+2。因此，三角形1由顶点集(p1,p2,p3)定义；三角形2的顶点次序为(p1, p3, p4);三角形3的顶点次序为(p1,p4,p5);而三角形4的顶点集为(p1，p5，p6)。