外罚函数与内罚函数

SUMT技术

之前的两篇blog讨论了等式最优化的最优性条件和不等式最优化的最优性条件。

（http://blog.csdn.net/ice110956/article/details/17557795 ）

（http://blog.csdn.net/ice110956/article/details/17562429 ）

关于无约束问题，我们通过最优性条件能够直接求出解，那么这种方法称为解析法。

但是，对于有约束问题的一般情况是，我们很难通过最优性条件来得到最优解。通常情况下，使用KKT条件求解时，我们要求与约束个数同阶的矩阵的逆。我们可以容易验证某个点是否是最优解，但是很难直接求解。

由于无约束的最优化问题我们已经有了许多高效的解法，于是，对于有约束的问题，我们可以转化为求解无约束问题，并且用迭代算法来求解。这么方法由称为序列无约束极小化技术SUMT（SequentialUnconstrained Minimization Technique）

 

外罚函数法

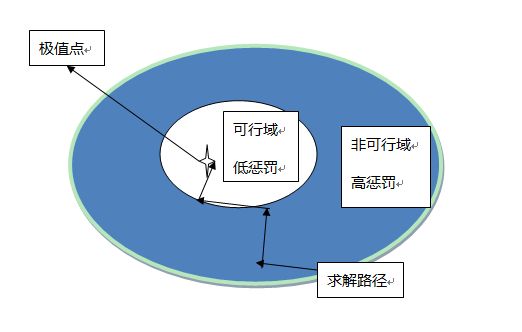
我们根据约束的特点，构造某种惩罚函数，然后加到目标函数中去，将约束问题求解转化为一系列的无约束问题。这种“惩罚策略”，对于无约束问题求解过程中的那些企图违反约束条件的目标点给予惩罚。如下图：

通过上述方法，我们可以把有约束的问题化为无约束问题求解。也就是我们的外罚函数法。

 

实例：

我们改写为无约束规划：

其中，我们设为非常大的数。

那么，当x1,x2不在可行域上时，后一项由于乘了,变为很大的数，对不在可行域上的点加以惩罚，迫使下一次迭代在可行域周围。

也就是，最优化（2）式的前一部分，得到最优解；最优化后一部分，使得解在可行域上。

那么（2）式得到的最优解，会是（1）式的最优解吗？外罚函数收敛吗？考虑到公式的数量与日志受欢迎程度成反比，这里直接给出结论：（2）式收敛，并且最优解为（1）式近似最优解。

 

具体算法：

我们用迭代算法来求解，这里直接给出迭代结束条件：。

经证明，外罚函数法式收敛的，上式也随着收敛到0.

当我们固定系数时，可求解无约束问题得到当前最优解，我们算出Xk之后，判断是否满足结束条件，满足则终止。否则修改惩罚力度，以xk为下一次初始点，，继续迭代。

步骤如下：

 

缺点：

1.由于上述都是近似最优并且近似可行的，近似最优可以接受，但是近似可行在实际运用中让人无法接受。这一点内罚函数可以解决；

2.根据收敛性，越大越好；但是我们直接求解时，用到求导以及hesse矩阵，越大，越趋于病态，也就是不好解，这是乘子法所要解决的问题。

 

内罚函数法

相比于外罚函数法在不可行区域加惩罚，内罚函数法在可行域边界筑起高墙，让目标函数无法穿过，就把目标函数挡在可行域内了。

这种惩罚策略只适用于不等式约束问题，并要求可行域的内点集非空，否则，每个可行点都是边界点，都加上无穷大惩罚，惩罚也就失去意义了。

考虑不等式约束：

当x从可行域

的内部趋近于边界时，则至少有一个ci(x)趋近于零，因此，不难想到可构造如下的增广的目标函数：

称为内罚函数或障碍函数，参数r仍称为罚因子。

上述的内罚函数，当x靠近边界时，会迅速增大，迫使在可行域之内进行求解。

如下图：

 

具体算法：

同外罚函数法类似，我们考虑用迭代算法来求解。每次变化得到一个罚因子rk,从前一步关于罚因子rk-1的最优解出发，得到下一步关于rk的最优解；当满足条件是，迭代结束，得到近似最优解。

经证明，内罚函数法也是收敛的，迭代结束的条件为

步骤如下：

 

小结

1）        由于无约束最优化问题的解法目前已有许多很有效的算法，如DFP，BFGS等，所以在求解复杂得多的约束优化问题是，工程技术人员一般乐于采用罚函数法——SUMT外点法和内点法。

2）        内点法适用于解含不等式约束问题，并且每次迭代的点都是可行点，这是设计人员所希望的。但要求初始点为可行域的内点，需要相当的工作量，同时它不能处理等式约束；外点法适于解既含等式约束又含不等式约束的优化问题，初始点可以是可行域之外的点，却不能保证近似最优解是可行的。

3）        罚函数法对于增广的目标函数的Hesse矩阵的条件数随罚因子增大或减小而增大，造成在求解无约束最优化问题时的困难，如何选择罚因子往往进退维谷。如外罚函数法，欲使得无约束问题接近于原约束问题，应该选择尽可能大的罚因子；但为了减轻求解无约束问题的困难，又应选取较小的罚因子，否则增广矩阵病态。这也是罚函数法的固有弱点。

解决这些问题，就要用到乘子法，关于乘子法，慢慢再整理出来。