全景图的种类及opencv实现

全景图概述

每当一个平面图像映射到一个弯曲的表面就会发生图象投影，反之亦然，这中现象特别常见于全景摄影。例如地球的球面可以映射到一块平坦的纸张。由于在我们周围的整个视场的可以被认为是作为球体的表面（对于所有观测角度），我们需要一种能将球形投影到2-D平面以便照片打印的方法。

小的视角相对容易进行形变并投影到平坦的纸上。但是，当试图把一个球形图像映射到一个平面上，有些变形是不可避免的。因此，每一种类型的投影仅仅尝试避免一种类型的失真，这是以牺牲其他失真为代价的。随着视场角增大，观测弧（viewing arc）变得更弯曲，从而全景投影类型之间的差异变得更加显着。什么时候使用那一种投影，在很大程度上取决于每个投影应用。 在这里，我们集中介绍在几个最常用。

全景图的种类

Equirectangular ： 将球形的经度和纬度坐标，直接到水平和垂直坐标的一格，这个网格的高度大约是宽的两倍。因此从赤道到两极，横向拉伸不断加剧，南北两个极点被拉伸成了扁平的网格在整个上部和下部边缘。 Equirectangular可以实现整个水平和竖直的360全景。

圆柱投影： 类似equirectangular，只是随着目标接近南北两极，纵向也会拉伸，两极会发生无限的纵向拉伸（因此这个扁平网格的顶部和底部没有水平线） 。由于这个原因，柱面投影不太适合具有非常大的垂直视角的图像。柱面投影是传统摆动镜头全景胶片相机所提供的标准投影方式。其对于目标尺寸的保持比直线投影更准确，然而这样就将平行于观测者视线的直线渲染成了曲线。

直线投影：主要优点在于，它把三维空间中的所有直线映射成二维网格上的直线。这种投影类型是大多数普通广角镜头所希望的，所以这也许是我们最熟悉的投影方式。它的主要缺点是，随着视角增加，它会大大加剧透视效果，从而导致在图像的边缘的对象产生歪斜。因此，对于远大于120度的全景图，一般不推荐直线投影。

直线投影：主要优点在于，它把三维空间中的所有直线映射成二维网格上的直线。这种投影类型是大多数普通广角镜头所希望的，所以这也许是我们最熟悉的投影方式。它的主要缺点是，随着视角增加，它会大大加剧透视效果，从而导致在图像的边缘的对象产生歪斜。因此，对于远大于120度的全景图，一般不推荐直线投影。

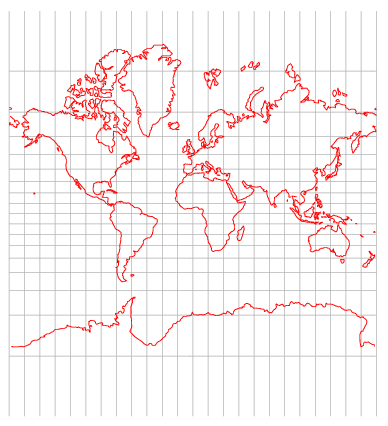
摩卡托投影：和圆柱以及equirectangular投影关系非常密切。是这两种类型之间的一种折衷。和柱面投影相比，其产生更小的垂直拉伸和更大的可用的垂直角度，但是直线会更加弯曲。这个投影方式最有名的应用就是在平面地图上，我们也注意到，这个方法的另一种变形：横轴摩卡托投影，可以被用于生成很高的纵向全景图。

正弦投影：目标是保持所有网格区域的面积。如果用这种投影将地球变平，可以使用反变换再次形成一个面积和形状不变的球体。面积相等的特性是非常有用的，因为其保持了一致的水平和竖直分辨率。此投影类似的鱼眼和立体图投影，但它保持了纬线的完全水平。

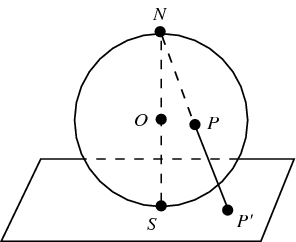
立体图投影：和鱼眼投影类似，但它通过随着目标远离透视中心，逐渐进行拉伸的方法，保持了更好的透视感。这种透视增长的特性有点类似与直线投影的效果。

OpenCV快速实现全景拼接

最新版的opencv2.4里面有很多新元素。 stitching module 就是一个非常有用的. 在opencv的例程文件夹里，有一个很好的脚本叫做 stitching_detailed.cpp. 这个脚本包括了创建全景图的全部过程，包括特征提取，匹配，warp，以及合成。安装好opencv以后，可以简单的通过命令行来测试这个例程：

$ ./stitching_detailed Univ*.jpg

这会使用默认参数来创建一个result.jpg的最终文件，来源的图片是以 "Univ"开头的jpg图像. 可以通过help察看一些设置

$ ./stitching_detailed --help

例如，可以改变投影的方式，默认是球面投影. 下面的例程用摩卡托投影法：

$ ./stitching_detailed Univ*.jpg --warp mercator

结果如下：原图像可以在这里找到

柱面

平面

摩卡托

参考文献：

http://www.cambridgeincolour.com

http://wiki.panotools.org

http://mathworld.wolfram.com

http://www.janeriksolem.net