深入浅出PID控制算法(一)————连续控制系统的PID算法及MATLAB仿真
引言
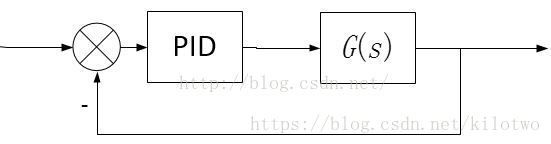
PID是Proportional(比例)、Integral(积分)、Differential(微分)三者的缩写。PID调节是连续控制系统中技术最成熟、应用最广泛的调节方式。PID调节实质是根据输入的偏差值,按照比例、积分、微分的函数关系进行运算,运算结果用以控制输出。
之前在项目中也用到过不少PID的算法,但大多属于一知半解的状态,或者胡乱调节的程度,最近在学习的过程偶然对PID有了一些新的认识,现在进行一些记录。
连续系统的PID控制
PID控制是将误差信号e(t)的比例(P),积分(I)和微分(D)通过线性组合构成控制量进行控制,其输出信号为:

对此式进行拉普拉斯变换,并且整理后得到模拟PID调节器的传递函数为:
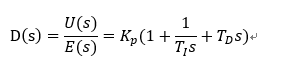
- Kp——比例系数
- Ti——积分时间常数
- Td——微分时间常数
- e(t)——偏差
- u(t)——控制量
对PID参数的简单理解
从上面的式子中可以看出
比例控制Kp能提高系统的动态响应速度,迅速反映误差,从而减少误差,但是不能消除误差,简单来说就是越大越快越小越慢但是可能会超调或者过慢有很多弊端,并且太大了会不稳定。
Ki为积分控制作用,一般就是消除稳态误差,只要系统存在误差积分作用就会不断积累,输出控制量来消除误差,如果偏差为零这时积分才停止,但是积分作用太强会使得超调量加大,甚至使系统出现震荡,那么问题来了,这个积分作用太强太弱是啥意思呢,我的理解是:积分作用就相当与容错率高的意思,你容错太多了才开始调节那不就是超调量太大了么,反之你容错率低,刚刚误差一点你就马上进行调节,这样不就容易引起震荡了嘛,所以不管怎么说这个积分调节都有点滞后的意思在里面,不管你容错多少这个误差都发生了,那么有没有办法对这种误差进行预测呢,就是需要微分环节了。
Kd为微分控制,微分显然与变化率有关,你可以把它理解为导数,它可以减小超调量来克服震荡,使系统稳定性提高,同时加快响应速度,使系统更快有更好的动态性能,这就像个“预言家”,它可以根据变化率来判断系统快要上升还是下降来提前改变系统的控制量这就与积分作用形成互补,这样一来系统就几乎完美了。
用MATLAB软件对PID控制做简单的仿真
说了这么多有些抽象,这就用matlab来简单仿真一下就明了了。
建立二阶负反馈控制系统,其开环传递函数为:

比例控制
输出与输入偏差成比例,即直接将误差信号放大或缩小。比例控制的传递函数为:
G(s)=Kp
取不同的比例系数,绘制系统的单位阶跃响应曲线:
Gs = tf(2,conv([3,1],[2,1])); %Gs是传递函数,conv是可以理解为因式分解(3s+1)(2s+1)
Kp = [0.5,2,5,10]; %取不同的比例系数,类似数组
for m = 1:4
sys = feedback(Kp(m)*Gs,1); %feedback(G,H),(G,H需事先设定)。
%其中G是传递函数,H为反馈函数,表示一个控制系统G,对其进行负反馈H(要求正反馈用-H)。这里前面写上比例环节与系统的串联,后面的1表示负反馈
step(sys); %求阶跃响应,可以用形如step(feedback(G,H))
hold on;
end
随着KP值的增大,系统响应速度加快,但系统的超调也随着增加,调节时间也随着增长。当KP增大到一定值后,闭环系统将趋于不稳定。
比例控制具有抗干扰能力强、控制及时、过渡时间短的优点,但存在稳态误差,增大比例系数可提高系统的开环增益,减小系统的稳态误差,从而提高系统的控制精度,但这会降低系统的相对稳定性,甚至可能造成闭环系统的不稳定,因此,在系统校正和设计中,比例控制一般不单独使用。
微分控制
输出与输入偏差的微分成比例,即与偏差的变化速度成比例。微分控制(与比例控制同时使用)的传递函数为:
G(s)=Kp(1+TdS)
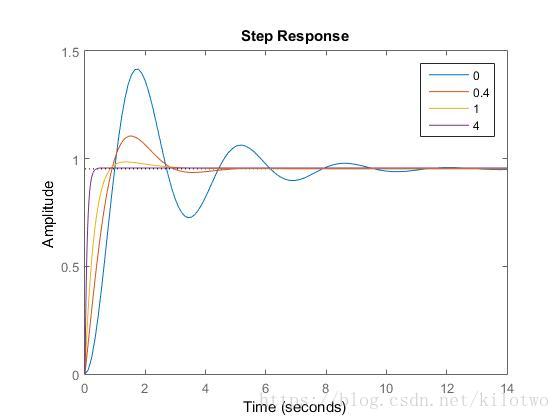
取不同的微分系数,绘制系统的单位阶跃响应曲线:
Kp = 10;
Td = [0,0.4,1,4];
for m = 1:4
G1 = tf([Kp*Td(m),Kp],[0,1]); %这个地方要注意 (Kp*Td(m)*S+Kp)/1=Kp(1+TdS)
sys = feedback(G1*Gs,1); %前面是微分环节与系统的串联,负反馈
step(sys); hold on;
end自动控制系统在克服误差的调节过程中可能会出现振荡甚至不稳定,原因是存在有较大惯性或有滞后的组件,具有抑制误差的作用,其变化总是落后于误差的变化,在控制器质中仅引入比例项是不够的,比例项的作用仅是放大误差的幅值,而微分项能预测误差的变化趋势,这样,具有比例+微分的控制器,就能提前使抑制误差的控制作用等于零,甚至为负值,从而避免被控量的严重超调,改善动态特性。
微分控制反映误差的变化率,只有当误差随时间变化时,微分控制才会对系统起作用,而对无变化或缓慢变化的对象不起作用。另外,微分控制对纯滞后环节不能起到改善控制品质的作用,反而具有放大高频噪声信号的缺点。
积分控制
输出与输入偏差的积分成比例,即与误差的积累成比例。积分控制(与比例控制同时使用)的传递函数为:
G(s)=Kp(1+1/Ti⋅1/s)
取不同的积分系数,绘制系统的单位阶跃响应曲线:
Kp = 2;
Ti = [3,6,12,24];
for m = 1:4
G1 = tf([Kp,Kp/Ti(m)],[1,0]); %这里也是(KpS+Kp/Ti)/s
sys = feedback(G1*Gs,1);
step(sys); hold on;
end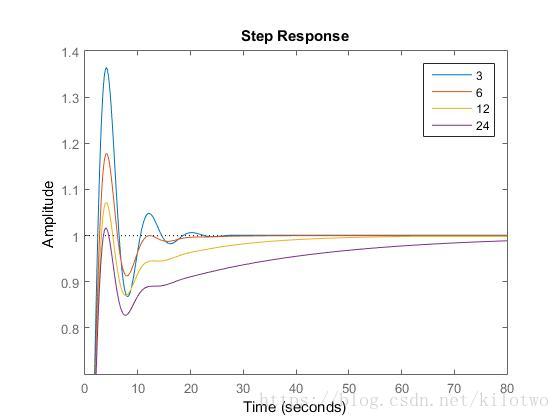
加入积分控制后,消除了系统稳态误差,但随着TI值的增大,达到稳态的过渡时间也逐渐加长。
积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。这样,即使误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大,使稳态误差进一步减小,直到等于零,但会使系统稳定性降低,过渡时间也加长。
比例积分微分控制,即PID控制
传递函数为:
G(s)=Kp(1+1/T⋅1/s+TdS)
取适当的比例、积分、微分系数,绘制系统的单位阶跃响应曲线:
Kp = 100; %取固定比例系数
Ti = 2.2;
Td =7;
G1 = tf([Kp*Td,Kp,Kp/Ti],[0,1,0]); %(Kp*Td*S^2+Kp*s+Kp/Ti)/s=Kp(Tds+1+1/STi)
sys = feedback(G1*Gs,1);
step(sys);
hold on;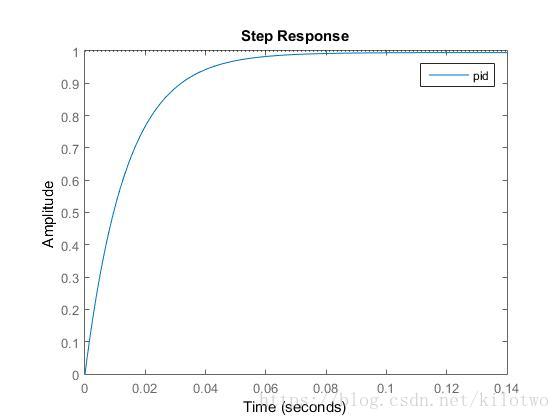
PID控制通过积分作用消除误差,而微分控制可缩小超调量、加快系统响应,是综合了PI控制和PD控制长处并去除其短处的控制。
Matlab-PID调节器
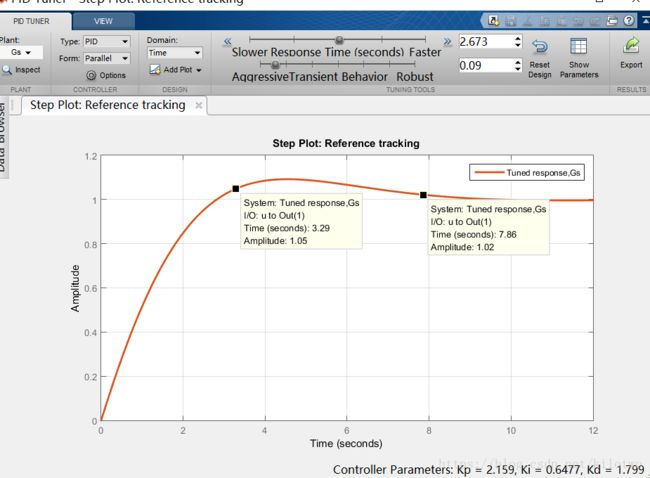
在较新版本的MATLAB中有应用程序,下有诸多的调节器,用起来简直不要太方便啊,简单介绍一下PID调节器,我的是R2015a:
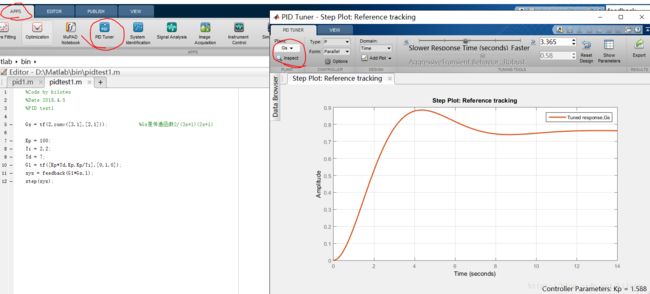
在已知被控对象传函的情况下,对单位负反馈中的PID进行调节,使得单位阶跃响应达到最佳。
点击Plant下的Import输入被调节对象的传函,传函是从matlab 工作区中选的,可以传入多个一起调节;
Type可以用来改变PID的类型(P/I/PI/PD/PID/PDF/PIDF);
Domain可以选择是时域调节还是频域调节,时域调节是调节response time(响应时间)和transient behavior(暂态特性),频域调节是调节bandwidth(带宽)和phase margin(相角裕度)。点击图标可以加快或者减慢调节;
show parameter可以看控制器的参数(窗口的最下端也有)和曲线的特性(超调量,稳定性等等);
Export选中想要获得的PID参数,可以输出到工作区中;
总结
本文对连续系统的PID控制从理论和实际的角度进行了剖析,并且学会了用Matlab进行仿真,可以看到Matlab可以方便的进行PID参数的整定调节,在实际操作前可以通过此来进行大量仿真来获得可靠的数据为调节和应用节约了大量成本。现在对PID有了初步的认识那么如何应用到程序中去呢,这就需要PID算法的离散化了,这将在后面的文章中进行讲解,谢谢你这么好看读完了这篇文章,希望对你有所帮助^_^.