【人工智能与机器学习 】第六周课后作业--牛顿法、梯度下降法的原理及使用方法
一、牛顿法
1.介绍
牛顿法(英语:Newton’s method)又称为牛顿-拉弗森方法(英语:Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。
一般情况对于f(x)是一元二次的情况直接应用求根公式就可以了,但是对于更高次(在5次方以上),没有求根公式,于是牛顿想了个近似求解的办法——牛顿法
2.求解方程
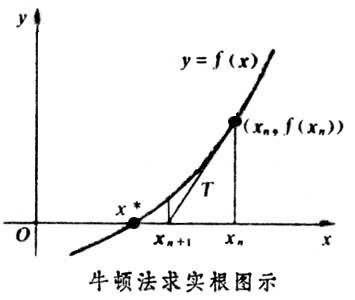
并不是所有的方程都有求根公式,或者求根公式很复杂,导致求解困难。利用牛顿法,可以迭代求解。原理是利用泰勒公式,在x0处展开,且展开到一阶,即f(x) = f(x0)+(x-x0)f’(x0)。求解方程f(x)=0,即f(x0)+(x-x0)f’(x0)=0,求解x = x1=x0-f(x0)/f’(x0),因为这是利用泰勒公式的一阶展开,f(x) = f(x0)+(x-x0)f’(x0)处并不是完全相等,而是近似相等,这里求得的x1并不能让f(x)=0,只能说f(x1)的值比f(x0)更接近f(x)=0,于是乎,迭代求解的想法就很自然了,可以进而推出x(n+1)=x(n)-f(x(n))/f’(x(n)),通过迭代,这个式子必然在f(x)=0的时候收敛。整个过程如下:
二、梯度下降法
1.介绍
梯度下降(gradient descent)在机器学习中应用十分的广泛,不论是在线性回归还是Logistic回归中,它的主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。
2.梯度下降算法
2.1场景假设
梯度下降法其实可以看成一个人下山的过程:假设一个场景,一个人被困在山上,此时起了大雾,他看不清楚下山的路径,就需要一步一步测量。此时下山就可以使用梯度下降法来帮助自己下山。
具体的方法:他可以先使用自己当前的位置为基准,找到这个位置最陡峭的地方,然后朝着下降的方向走一步,然后又继续以此时的位置为基准,找到最陡峭的地方,再走,再找最陡峭的地方,直到走到最低点位置。
![]()
2.2梯度下降
和下山类似,首先需要一个可以微分的函数,这个函数就是上文中的“山”,我们需要“下山”,走到“山”的最低点,就是找到该函数的最小值。根据上文场景假设,最快的下山方式就是找到当前位置的最陡峭位置,然后走到该位置后又继续上面的步骤,在函数中就是找到给定点的梯度,朝着梯度相反的方向,就可以让函数值下降的最快!因为梯度的方向就是函数变化最快的方向!所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。
三、实际操作
使用jupyter notebook运行梯度下降法实例代码:
首先,定义数据集和学习率
from numpy import *
# 数据集大小 即20个数据点
m = 22
# x的坐标以及对应的矩阵
X0 = ones((m, 1)) # 生成一个m行1列的向量,也就是x0,全是1
X1 = arange(1, m+1).reshape(m, 1) # 生成一个m行1列的向量,也就是x1,从1到m
X = hstack((X0, X1)) # 按照列堆叠形成数组,其实就是样本数据
# 对应的y坐标
y = np.array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21,
22,23
]).reshape(m, 1)
# 学习率
alpha = 0.01
接下来以矩阵向量的形式定义代价函数和代价函数的梯度:
# 定义代价函数
def cost_function(theta, X, Y):
diff = dot(X, theta) - Y # dot() 数组需要像矩阵那样相乘,就需要用到dot()
return (1/(2*m)) * dot(diff.transpose(), diff)
# 定义代价函数对应的梯度函数
def gradient_function(theta, X, Y):
diff = dot(X, theta) - Y
return (1/m) * dot(X.transpose(), diff)
最后就是算法的核心部分,梯度下降迭代计算
# 梯度下降迭代
def gradient_descent(X, Y, alpha):
theta = array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, Y)
while not all(abs(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, Y)
return theta
optimal = gradient_descent(X, Y, alpha)
print('optimal:', optimal)
print('cost function:', cost_function(optimal, X, Y)[0][0])
当梯度小于1e-5时,说明已经进入了比较平滑的状态,类似于山谷的状态,这时候再继续迭代效果也不大了,所以这个时候可以退出循环!
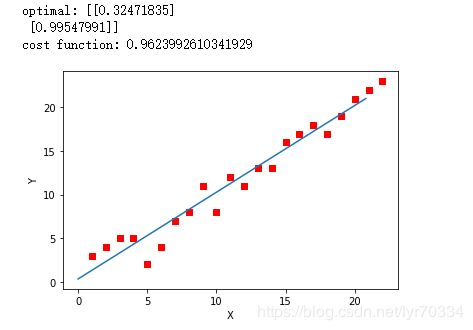
运行代码,计算得到的结果如下:
print('optimal:', optimal) # 结果 [[0.32471835][0.99547991]]
print('cost function:', cost_function(optimal, X, Y)[0][0]) # 0.9623992610341929
通过matplotlib画出图像
# 根据数据画出对应的图像
def plot(X, Y, theta):
import matplotlib.pyplot as plt
ax = plt.subplot(111) # 这是我改的
ax.scatter(X, Y, s=30, c="red", marker="s")
plt.xlabel("X")
plt.ylabel("Y")
x = arange(0, 21, 0.2) # x的范围
y = theta[0] + theta[1]*x
ax.plot(x, y)
plt.show()
plot(X1, Y, optimal)
结果如图:
全部代码:
from numpy import *
# 数据集大小 即22个数据点
m = 22
# x的坐标以及对应的矩阵
X0 = ones((m, 1)) # 生成一个m行1列的向量,也就是x0,全是1
X1 = arange(1, m+1).reshape(m, 1) # 生成一个m行1列的向量,也就是x1,从1到m
X = hstack((X0, X1)) # 按照列堆叠形成数组,其实就是样本数据
# 对应的y坐标
Y = array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21,
22,23
]).reshape(m, 1)
# 学习率
alpha = 0.01
# 定义代价函数
def cost_function(theta, X, Y):
diff = dot(X, theta) - Y # dot() 数组需要像矩阵那样相乘,就需要用到dot()
return (1/(2*m)) * dot(diff.transpose(), diff)
# 定义代价函数对应的梯度函数
def gradient_function(theta, X, Y):
diff = dot(X, theta) - Y
return (1/m) * dot(X.transpose(), diff)
# 梯度下降迭代
def gradient_descent(X, Y, alpha):
theta = array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, Y)
while not all(abs(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, Y)
return theta
optimal = gradient_descent(X, Y, alpha)
print('optimal:', optimal)
print('cost function:', cost_function(optimal, X, Y)[0][0])
# 根据数据画出对应的图像
def plot(X, Y, theta):
import matplotlib.pyplot as plt
ax = plt.subplot(111)
ax.scatter(X, Y, s=30, c="red", marker="s")
plt.xlabel("X")
plt.ylabel("Y")
x = arange(0, 21, 0.2) # x的范围
y = theta[0] + theta[1]*x
ax.plot(x, y)
plt.show()
plot(X1, Y, optimal)
参考文献链接:
1.Newton法(牛顿法 Newton Method)
2.什么是梯度下降法?
3.梯度下降算法原理讲解——机器学习