维特比算法（HMM预测问题）与Python实现

1 前言

这里介绍维特比算法，主要是其在解决HMM模型中预测问题中起到了很大得作用，之前也粗略介绍过维特比算法：维特比算法
但是不是很详细，这里再详细介绍一下。HMM预测问题也称为解码(decoding)问题。已知模型$\lambda =(A,B,\pi )$和观测序列$O=(o_1,o_2,\cdots ,o_T)$，求给定的观测序列条件概率$P(I|O)$最大的状态序列$I=(i_1,i_2,\cdots ,i_T)$。即给定观测序列，求最有可能的对应的状态序列。对于该问题，有两种算法：近似算法与维特比算法（Viterbi algorithm），我们主要是维特比算法。

维特比算法实际是用动态规划解隐马尔科夫模型预测问题，即用动态规划(dynamic programming)求概率最大路径（最优路径）。这时一条路径对应着一个状态序列。

2 维特比算法

输入：模型$\lambda =(A,B,\pi )$和观测序列$O=(o_1,o_2,\cdots ,o_T)$;

输出：最优路径$I^{\ast }=(i_1^{\ast },i_2^{\ast },\cdots ,i_T^{\ast })$。

(1) 初始化：

${\delta }_1(i)={\pi }_i{b}_i(o_1),i=1,2,\dots ,N$

${\Psi }_1(i)=0,i=1,2,\cdots ,N$

(2)递推.对t=2,3,…,T

${\delta }_t(i)=\underset{1\le j\le N}{\max }[{\delta }_{i-1}(j)a_{j_i}]b_i(o_i),i=1,2,\dots ,N$

${\Psi }_t(i)=arg\underset{1\le j\le N}{\max }[{\delta }_{t-1}{a}_{ji}],i=1,2,\dots ,N$

需要注意的是${\Psi }_t(i)$面向得是t-1时刻得到当前得转移率，并没有与状态概率相乘。

(3) 终止

$P^{\ast }=\underset{1\le i\le N}{\max }{\delta }_T(i)$

$i_T^{\ast }=arg\underset{1\le i\le N}{\max }[{\delta }_T(i)]$

例：HMM模型$\lambda =(A,B,\pi )$，题目再述：有三个盒子，每个盒子中有红、白两种球，其中专业概率相关参数如下：。
$$A=\left[\begin{array}{ccc}0.5& 0.2& 0.3\\ 0.3& 0.5& 0.2\\ 0.2& 0.3& 0.5\end{array}\right],B=\left[\begin{array}{cc}0.5& 0.5\\ 0.4& 0.6\\ 0.7& 0.3\end{array}\right]$$
已知观测序列$O=(红，白，红)$，试求最优状态序列，即最优路径$I^{\ast }=(i_1^{\ast },i_2^{\ast },i_3^{\ast })$.

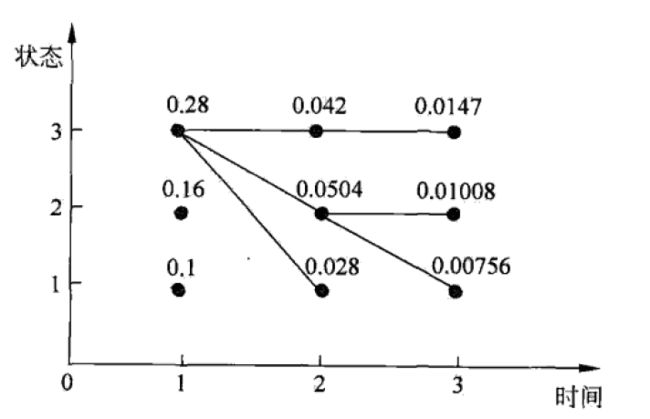
解：如下图所示，要在所有可能的路径中选择一条最优路径，求状态i观测$o_1$为红的概率，记此概率为${\delta }_1(i)$，则

(1)初始化.在t=1时，对每一个状态i，i=1,2,3,求状态为i观测$o_1$为红球的概率，记此概率为${\delta }_1(i)$，上例已知：$\pi =(0.2,0.4,0.4{)}^T$则：

${\delta }_1(i)={\pi }_i{b}_i(o_1)={\pi }_i(红),i=1,2,3$

带入实际数据：

${\delta }_1(1)=0.2\times 0.5=0.10,{\delta }_1(2)=0.4\times 0.4=0.16,{\delta }_1(3)=0.4\times 0.7=0.28$

记$\Psi (i)=0,i=1,2,3$.

(2)在t=2时，对每个状态i, i=1,2,3,求在t=1时状态j观测为红并在t=2时状态为i观测$o_2$为白的路径的最大概率，记此最大概率为${\delta }_2(i)$，则：

${\delta }_2(i)=\underset{1\le j\le 3}{\max }[{\delta }_1(j)a_{ji}]b_i(o_2)$

同时，对每个状态i,i=1,2,3,记录概率最大路径的的前一个状态j:

${\Psi }_2(i)=arg\underset{1\le j\le 3}{\max }[{\delta }_1(j)a_{ji}],i=1,2,3$

计算有：
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ \delta_2(1) &=…
需要注意的是：在t=2也有三个状态的可能性。其中${\delta }_2(1)$表示从t=1的各个可能的状态到t=2 状态为1观测为白的最大值。${\Psi }_2(i)=3,i=1,2,3$是因为，当前路径中，上一个状态中状态3的概率最大，这里记住上一个状态，以便回溯。这里计算${\Psi }_2(i)$不是很清楚，以${\Psi }_2(1)$计算为例，如下：
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ \Psi_2(1)&=arg…
可得当i=3时取最大，即有${\Psi }_2(1)=3$

同样，在t=3时，
$$\begin{gathered} {\delta }_3(i)=\underset{1\le j\le 3}{\max }[{\delta }_2(j)a_{ji}]b_i(o_3) \\ {\Psi }_3(i)=arg\underset{1\le j\le 3}{\max }[{\delta }_2(j)a_{ji}] \\ {\delta }_3(1)=0.00756,{\Psi }_3(1)=2 \\ {\delta }_3(2)=0.01008,{\Psi }_3(2)=2 \\ {\delta }_3(3)=0.0147,{\Psi }_3(3)=3 \end{gathered}$$
(3)以$P^{\ast }$表示最优路径的概率，则：

$P^{\ast }=\underset{1\le i\le 3}{\max }{\delta }_3(i)=0.0147$

最优路径的终点是$i_3^{\ast }$:$i_3^{\ast }=arg\underset{i}{\max }[{\delta }_3(i)]=3$

(4)由最优路径的终点$i_3^{\ast }$,逆向查找$i_2^{\ast },i_1^{\ast }$:

在t=2时，$i_2^{\ast }={\Psi }_3(i_3^{\ast })={\Psi }_3(3)=3$

在t=1时，$i_1^{\ast }={\Psi }_2(i_2^{\ast })={\Psi }_2(3)=3$

于是求得最优路径，即最优状态序列$I^{\ast }=(i_1^{\ast },i_2^{\ast },i_3^{\ast })=(3,3,3)$

3 Python 实现

以下代码是个人根据李航老师那本书进行书写的，也难免有些bug，如果有的话，也希望各位友友提出，共同学学习和进步。

def viterbi(A, B, Pi, Obser, state):
    """
    计算预测状态
    :para:A 状态转移矩阵
    :para:B 发射矩阵
    :para:Pi 初始化矩阵
    :para:Obser 观测序列
    :parar:state 状态集合
    :return: 返回两个值，第一个值是整个过程的维特比计算矩阵，第二个是预测序列的索引
    """
    import numpy as np
    row, col = len(Obser), len(state)
    res = np.zeros((row, col))      # 竖向矩阵
    res2 = np.zeros_like(res)
    # print(res2)
    # 转换为矩阵计算
    A, B, Pi = np.array(A), np.array(B), np.array(Pi)
    # 初始化
    res[0, :] = B.T[0]*Pi
    # 后续循环状态(2-t状态)
    for i in range(1, row):
        # 循环隐藏状态数，计算当前状态每个隐藏状态的概率
        ob = Obser[i]     # 当前观察值
        tempres, tempres2 = [], []
        for j in range(col):
            # 以盒子1为例， 其他盒子转移到盒子
            # print(A[:, j])     # 表示A中的第j列数据, 即其他盒子转移到盒子j的概率
            # print(res[i - 1])  # res中第i-1行数的值 即delta(i-1)
            # print(B[:, ob])    # 发射矩阵中的第ob列（由观测值确定）
            # delta j的计算
            delta = A[:, j]*res[i - 1]*B[j][ob]
            # Psi # 获取最大值的索引
            tempres2.append(np.argmax(A[:, j]*res[i - 1]))
            tempres.append(np.max(delta))
        res[i, :] = np.array(tempres)  # 结果矩阵赋值
        res2[i, :] = np.array(tempres2)
    # 通过res和res2回溯
    result = []
    # 最后一行直接计算
    result.append(np.argmax(res[row-1, :]))
    i = row - 1
    while i > 0:
        result.append(res2[i][np.argmax(res[i, :])])
        i -= 1
    result.reverse()   # 我们是逆向添加的
    return res, result


if __name__ == "__main__":
    # 隐藏状态, 为方便计算这里将隐层
    invisiable = {0: '盒子1', 1: '盒子2', 2: '盒子3'}
    invisiable_ls = [0, 1, 2]
    # 初始状态 pi
    pi = [0.2, 0.4, 0.4]
    # 转移矩阵 A
    trainsion_probility = [
        [0.5, 0.2, 0.3],
        [0.3, 0.5, 0.2],
        [0.2, 0.3, 0.5]
    ]
    # 发射矩阵B
    emission_probility = [
        [0.5, 0.5],
        [0.4, 0.6],
        [0.7, 0.3]
    ]
    # 观测序列
    obs_dic = {0: "红", 1: "白"}
    # obs_seq = [0, 1, 0, 1, 0, 0, 0, 1, 1, 1]
    obs_seq = [0, 1, 0]
    print("观测序列为：")
    for i in obs_seq:
        print(obs_dic[i], end=" ")
    print("")
    # 结果
    res, result = viterbi(trainsion_probility, emission_probility, pi, obs_seq, invisiable_ls)
    print("res:\n", res)
    print("预测序列为：")
    for i in result:
        print(invisiable[i], end=" ")

输出结果：

观测序列为：
红 白 红
res:
 [[0.1     0.16    0.28   ]
 [0.028   0.0504  0.042  ]
 [0.00756 0.01008 0.0147 ]]
预测序列为：
盒子3 盒子3 盒子3

Reference

李航的《统计机器学习》
个人订阅号
更多算法知识等着你