线性规划之单纯形解法Java实现
单纯形法
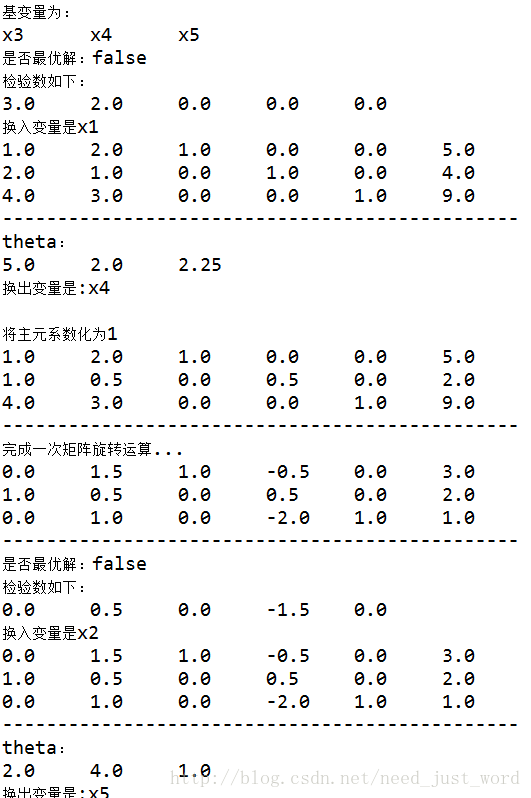
理解完这个算法后大家也可以打一下,打码过程中,会有很多很多的错误要排查,编码一小时,排错三小时,不过从中可以练习到蛮多的(运行截图在文末)
- 输入线性规划标准型的数据(n个变量,m个约束条件)
- C //价值系数向量
- X //决策变量向量
- A //工艺系数矩阵
- b //资源常数
- yita //检验数
- theta //b除以换入变量在每行的系数,即单纯形表最右端参数
找基可行解
- 简单的拿最后m个决策变量,后期可优化
判断是否最优解:计算并判断是否每一个检验数yita都小于等于0
- 是
- 输出最优解:max z = CX
- 否
- 确定换入变量
- 检验数大于0中,检验数最大的非基变量
- 确定换出变量
- 计算theta
- 判断是否线性规划结果为无界解:theta的系数是否均小于或等于0
- 是
- 终止运算,输出结果为无界解
- 否
- 取theta[i]中大于0且最小的行所对应的基变量作为换出变量
- 是
- 旋转运算
- 换入变量的所对应的方程中左右两边同除换入变量的系数
- 再次循环,重新判断是否最优解
- 确定换入变量
- 是
所有函数
- void inputNums() //输入数据
- void findBasedVariables() //找基变量
- bool isOptimum() //是否最优解
- int getVariableIn() //确定换入变量
- int getVariableOut() //确定换出变量
- void updateVectors() //更新旋转运算后的矩阵
- private static void printVector() //输出系数矩阵
- void printOptimun() //输出最优解
先在main函数中写好主要逻辑,再具体实现
public static void main(String[] args) {
//输入数据,为了简单起见,我们的数据直接在代码中敲入,这个函数等测试完后加
inputNums();
//找初始基变量
findBasedVariables();
//判断是否最优解
while (!isOptimum()) {
//找换入变量
idxOfIn = getVariableIn();
printVector();
//找换出变量
idxOfOut = getVariableOut();
//如果idxOfOut返回-1,则该线性规划问题有无界解
if(idxOfOut == -1)
return;
//旋转运算,更新矩阵
updateVectors();
printVector();
System.out.println("\n");
}
//输出最优解
printOptimum();
}全局变量
private static double A[][] = { { 1, 2, 1, 0, 0 },
{ 2, 1, 0, 1, 0 },
{ 4, 3, 0, 0, 1 } };// 系数矩阵
private static int m = A.length; //m个方程
private static int n = A[0].length; //n个决策变量
private static double C[] = { 3, 2, 0, 0, 0 }; // 价值系数
private static double b[] = { 5, 4 ,9}; // 资源常数
private static double theta[] = new double[m]; //b的检验数
private static int basedVar[] = new int[m]; // 基变量,存基变量的下标,从1开始标号(区别于数组存储习惯)
private static double yita[] = new double[n]; //检验数,有n个决策变量的检验数
private static double result = -1; //结果
private static int idxOfIn = -1; //换入变量的下标
private static int idxOfOut = -1; //换出变量的下标inputNums()
// 输入数据,先在代码中写入数据,后期再加,先把初始检验数赋值为价值系数
private static void inputNums() {
for (int i = 0; i < yita.length; i++) {
yita[i] = C[i]; //yita为检验数
}
}findBasedVariables()
// 找基变量,简单的拿最后m个决策变量,后期可优化,存储在basedVar数组中
private static void findBasedVariables() {
//取n个决策变量的最后m个作基变量
for (int i = 0; i < m; i++) {
//basedVar[i] = n-i;
//改变存放顺序为正叙
basedVar[m-i-1] = n-i ;
}
System.out.println("基变量为:");
for (int i = 0; i < basedVar.length; i++) {
System.out.print("x" + (basedVar[i]) + "\t");
}
System.out.println();
}isOptimum()
// 判断是否最优解,并计算检验数yita向量
private static boolean isOptimum() {
//换入变量代替换出变量
if(idxOfIn != -1 && idxOfOut != -1){
//第idxOfOut个基变量换为x idxOfIn
basedVar[idxOfOut] = idxOfIn+1;
}
//更新检验数
for (int i = 0; i < n; i++) {
double temp = yita[i];
for (int j = 0; j < m; j++) {
temp -= A[j][i] * C[basedVar[j] -1];
}
yita[i] = temp;
}
boolean hasPossitiveYita = false;
for (int i = 0; i < yita.length; i++) {
if(yita[i] > 0)
hasPossitiveYita = true;
}
System.out.println("是否最优解:" + !hasPossitiveYita);
return !hasPossitiveYita;
}getVariableIn()
// 确定换入变量,返回换入变量的下标-1
private static int getVariableIn() {
//遍历检验数
int index = 0;
System.out.println("检验数如下:");
for (int i = 0; i < yita.length; i++) {
System.out.print(yita[i] + "\t");
if(yita[i] > yita[index]){
index = i;
}
}
System.out.println();
System.out.println("换入变量是x" + (index+1));
return index;
}getVariableOut()
// 确定换出变量,返回换出变量在基变量向量中的下标
private static int getVariableOut() {
System.out.println("theta:");
for (int i = 0; i < m; i++) {
if( Double.compare(A[i][idxOfIn], 0) != 0)
theta[i] = b[i] / A[i][idxOfIn];
else {
theta[i] = 0;
}
System.out.print(theta[i] + "\t");
}
System.out.println();
int index = 0;
for (int i = 0; i < theta.length; i++) {
if(theta[i] <= 0){
System.out.println("该方程有无界解...");
return -1;
}else {
if(theta[i] < theta[index])
index = i;
}
}
System.out.println("换出变量是:x" + (basedVar[index]));
return index;
}updateVectors()
// 更新旋转运算后的矩阵
private static void updateVectors() {
//m个方程,n个变量
//将主元系数化为1
//防止迭代中主元的值被改变后引起 其它系数除主元的新值,将主元的原值存于temp
double temp = A[idxOfOut][idxOfIn];
for (int i = 0; i < n; i++) {
A[idxOfOut][i] /= temp;
}
b[idxOfOut] /= temp;
System.out.println("\n将主元系数化为1");
printVector();
//主元所在列其余元素系数要化为0,即:主元列中,非主元所在行均减去 主元系数分之一*A[m][n]
for (int i = 0; i < m; i++) {
//若是换出变量所对应行,则该行不用换算
double temp1 = A[i][idxOfIn]/A[idxOfOut][idxOfIn];
if(i != idxOfOut){
for (int j = 0; j < n; j++) {
A[i][j] -= A[idxOfOut][j]*temp1;
}
b[i] -= b[idxOfOut] * temp1;
}
}
System.out.println("完成一次矩阵旋转运算...");
}printVector()
//输出系数矩阵
private static void printVector() {
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(A[i][j] + "\t");
}
System.out.println(b[i]);
}
System.out.println("-----------------------------------------------");
}printOptimum()
//输出最优解
private static void printOptimum() {
result = 0;
for (int i = 0; i < basedVar.length; i++) {
result += C[basedVar[i]-1] * b[i];
}
System.out.println("最优解:z = " + result);
}