一 . 暴力破解与实用性优先
做题目时:能枚举就枚举,能逆向就逆向,先试探一个解。
1. 猜年龄
【问题描述】美国数学家维纳(N.Wiener)智力早熟,11岁就上了大学。
他曾在1935~1936年应邀来中国清华大学讲学。
一次,他参加某个重要会议,年轻的脸孔引人注目。
于是有人询问他的年龄,他回答说:
“我年龄的立方是个4位数。我年龄的4次方是个6位数。这10个数字正好包含了从0到9这10个数字,每个都恰好出现1次。”
请你推算一下,他当时到底有多年轻。
(恰好出现一次:即代码中需要:①检测不重复 ②检测不遗漏)
暴力破解的框架是(利用位数信息):
for(int i=0;i<100;i++){
s=把立方与四次方拼串
if(test(s)==false) continue;
print(i);
}
【源代码】
【JAVA:于航】
public class A{
public static void main(String[] args){
for(int i=1; i<100; i++){
int a = i * i * i;
int b = a * i;
if((a+"").length()!=4) continue;
if((b+"").length()!=6) continue;
System.out.println(i + " = " + a + " " + b);
}
}
}
2. 罗马数字
【问题描述】古罗马帝国开创了辉煌的人类文明,但他们的数字表示法的确有些繁琐,尤其在表示大数的时候,现在看起来简直不能忍受,所以在现代很少使用了。
之所以这样,不是因为发明表示法的人的智力的问题,而是因为一个宗教的原因,当时的宗教禁止在数字中出现0的概念!
罗马数字的表示主要依赖以下几个基本符号:
I –> 1
V –> 5
X –> 10
L –> 50
C –> 100
D –> 500
M –> 1000
这里,我们只介绍一下1000以内的数字的表示法。
单个符号重复多少次,就表示多少倍。最多重复3次。
比如:CCC表示300 XX表示20,但150并不用LLL表示,这个规则仅适用于I X C M。
如果相邻级别的大单位在右,小单位在左,表示大单位中扣除小单位。
比如:IX表示9 IV表示4 XL表示40
49 = XLIX
更多的示例参见下表,你找到规律了吗?
I = 1
II = 2
III = 3
IV = 4
V = 5
VI = 6
VII = 7
VIII = 8
IX = 9
X = 10
XI = 11
XII = 12
XIII = 13
XIV = 14
XV = 15
XVI = 16
XVII = 17
XVIII = 18
XIX = 19
XX = 20
XXI = 21
XXII = 22
XXIX = 29
XXX = 30
XXXIV = 34
XXXV = 35
XXXIX = 39
XL = 40
L = 50
LI = 51
LV = 55
LX = 60
LXV = 65
LXXX = 80
XC = 90
XCIII = 93
XCV = 95
XCVIII = 98
XCIX = 99
C = 100
CC = 200
CCC = 300
CD = 400
D = 500
DC = 600
DCC = 700
DCCC = 800
CM = 900
CMXCIX = 999
本题目的要求是:请编写程序,由用户输入若干个罗马数字串,程序输出对应的十进制表示。
输入格式是:第一行是整数n,表示接下来有n个罗马数字(n<100)。
以后每行一个罗马数字。罗马数字大小不超过999。
要求程序输出n行,就是罗马数字对应的十进制数据。
例如,用户输入:
3
LXXX
XCIII
DCCII
则程序应该输出:
80
93
702
特殊情况是有限种:IV:4 IX:9 XL:40 XC:90 CD:400 CM:900
因此,并不总是需要找出相应的规律 当情况没有成千上万那么多时,使用 枚举法 更高效与稳定
【源代码】
【JAVA:于航】
//罗马数字的枚举解法
public class A{
public static int romeNum(String s){
int sum = 0;
for(int i=0; i
if(s.indexOf("IX")>=0) sum -= 2;
if(s.indexOf("XL")>=0) sum -= 20;
if(s.indexOf("XC")>=0) sum -= 20;
if(s.indexOf("CD")>=0) sum -= 200;
if(s.indexOf("CM")>=0) sum -= 200;
return sum;
}
public static void main(String[] args){
System.out.println(romeNum("MCCCXIV"));
System.out.println(romeNum("CMXCIX"));
}
}
//罗马数字的逆向解法:将十进制的数字拆分成个位、十位、百位、千位等,再进行枚举的转换
public class NiXiang
{
static String NumRoman(int x){
int a = x / 1000; // 千位
int b = x % 1000 / 100; //百位
int c = x % 100 / 10; // 十位
int d = x % 10;
String s = "";
if(a==1) s += "M";
if(a==2) s += "MM";
if(a==3) s += "MMM";
if(b==1) s += "C";
if(b==2) s += "CC";
if(b==3) s += "CCC";
if(b==4) s += "CD";
if(b==5) s += "D";
if(b==6) s += "DC";
if(b==7) s += "DCC";
if(b==8) s += "DCCC";
if(b==9) s += "CM";
if(c==1) s += "X";
if(c==2) s += "XX";
if(c==3) s += "XXX";
if(c==4) s += "XL";
if(c==5) s += "L";
if(c==6) s += "LX";
if(c==7) s += "LXX";
if(c==8) s += "LXXX";
if(c==9) s += "XC";
if(d==1) s += "I";
if(d==2) s += "II";
if(d==3) s += "III";
if(d==4) s += "IV";
if(d==5) s += "V";
if(d==6) s += "VI";
if(d==7) s += "VII";
if(d==8) s += "VIII";
if(d==9) s += "IX";
return s;
}
//判断输出格式的错误
static boolean RomanNumOK(String s){
for(int i=0; i<4000; i++){
if(s.equals(NumRoman(i))) return true;
}
return false;
}
public static void main(String[] args){
System.out.println(RomanNumOK("CCXLIX"));
System.out.println(RomanNumOK("CCXXLIX"));
//System.out.println(NumRoman(3009));
}
}
3. 九宫幻方
【问题描述】小明最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分。
三阶幻方指的是将1~9不重复的填入一个3*3的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。
三阶幻方又被称作九宫格,在小学奥数里有一句非常有名的口诀:
“二四为肩,六八为足,左三右七,戴九履一,五居其中”,
通过这样的一句口诀就能够非常完美的构造出一个九宫格来。
4 9 2
3 5 7
8 1 6
有意思的是,所有的三阶幻方,都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。
现在小明准备将一个三阶幻方(不一定是上图中的那个)中的一些数抹掉,交给邻居家的小朋友来进行还原,并且希望她能够判断出究竟是不是只有一个解。
而你呢,也被小明交付了同样的任务,但是不同的是,你需要写一个程序~
输入格式:
输入仅包含单组测试数据。
每组测试数据为一个3*3的矩阵,其中为0的部分表示被小明抹去的部分。
对于100%的数据,满足给出的矩阵至少能还原出一组可行的三阶幻方。
输出格式:
如果仅能还原出一组可行的三阶幻方,则将其输出,否则输出“Too Many”(不包含引号)。
样例输入
0 7 2
0 5 0
0 3 0
样例输出
6 7 2
1 5 9
8 3 4
三阶幻方翻转或镜像变换共有8种情况(翻转得到4种 镜像变换得到四种)
【源代码】
【JAVA:于航】
/*
4 9 2
3 5 7
8 1 6
"492357816"
8 3 4
1 5 9
6 7 2
"834159672"
0 7 2
0 5 0
0 3 0
*/
public class A
{
static boolean test(String std, String s){
for(int i=0; i
if(s.charAt(i)=='0') continue;
return false;
}
return true;
}
public static void main(String[] args){
String s = "072050030";
String[] ss = {
"492357816",
"834159672",
"618753294",
"276951438",
"294753618",
"438951276",
"816357492",
"672159834"
};
for(int i=0; i
System.out.println(ss[i].substring(0,3));
System.out.println(ss[i].substring(3,6));
System.out.println(ss[i].substring(6,9));
}
}
}
}
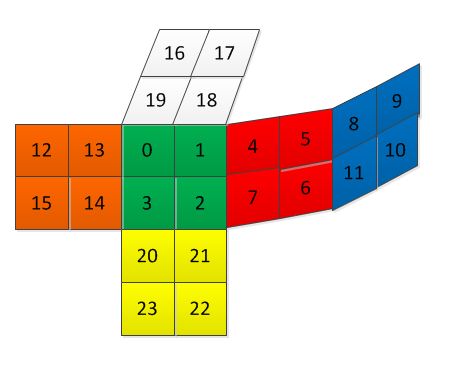
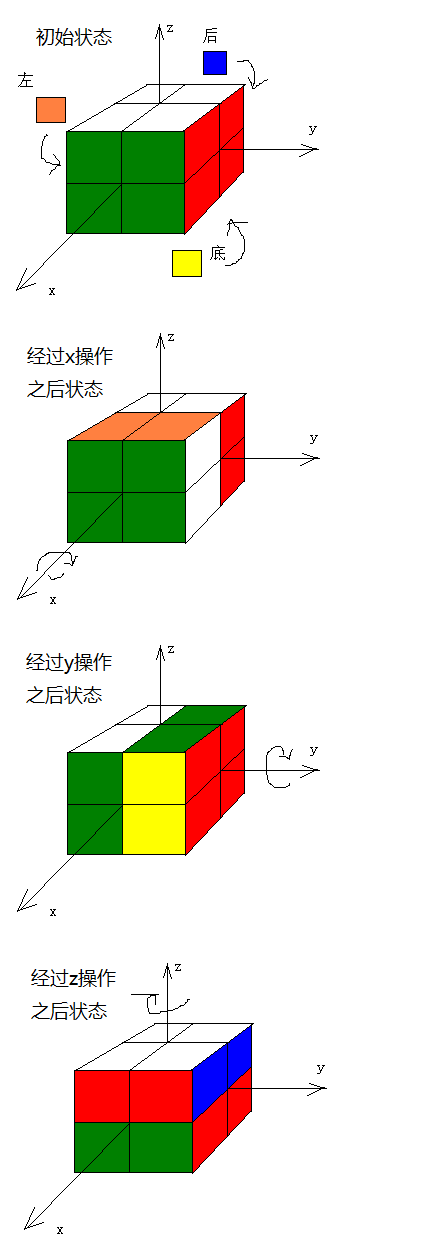
4. 魔方旋转
【问题描述】魔方可以对它的6个面自由旋转。
我们来操作一个2阶魔方(如图1所示):
为了描述方便,我们为它建立了坐标系。
各个面的初始状态如下:
x轴正向:绿
x轴反向:蓝
y轴正向:红
y轴反向:橙
z轴正向:白
z轴反向:黄
假设我们规定,只能对该魔方进行3种操作。分别标记为:
x 表示在x轴正向做顺时针旋转
y 表示在y轴正向做顺时针旋转
z 表示在z轴正向做顺时针旋转
xyz 则表示顺序执行x,y,z 3个操作
题目的要求是:
用户从键盘输入一个串,表示操作序列。
程序输出:距离我们最近的那个小方块的3个面的颜色。
顺序是:x面,y面,z面。
例如:在初始状态,应该输出:
绿红白
初始状态下,如果用户输入:
x
则应该输出:
绿白橙
初始状态下,如果用户输入:
zyx
则应该输出:
红白绿
使用一维数组存储数据,定义三个方法,实现x,y,z 旋转操作,将位置更改。
【源代码】【JAVA:于航】
/*
二阶魔方的各个面给一个唯一编号:(最中间为绿 )
16 17
19 18(白)
-------
(橙) 12 13 | 0 1 | 4 5 | 8 9 (蓝)
15 14 | 3 2 | 7 6 | 11 10
-------(红)
(黄)20 21
23 22
上
左前右后
下
x操作:(0,1,2,3) (4,21,14,19) (7,20,13,18)
y操作:(4,5,6,7) (1,17,11,21) (2,18,8,22)
z操作:(16,17,18,19) (0,12,8,4) (1,13,9,5)
每种操作引发了三个轮换
*/
public class A
{
static int[][] transx={{0,1,2,3},{4,21,14,19},{7,20,13,18}};
static int[][] transy={{4,5,6,7},{1,17,11,21},{2,18,8,22}};
static int[][] transz={{16,17,18,19},{0,12,8,4},{1,13,9,5}};
static char[] op(char[] a,int[][] trans){
char[] b = java.util.Arrays.copyOf(a,a.length);
for(int i=0; i
b[trans[i][2]] = a[trans[i][1]];
b[trans[i][3]] = a[trans[i][2]];
b[trans[i][0]] = a[trans[i][3]];
}
return b;
}
static char[] op(char[] a, String s){
char[] b = java.util.Arrays.copyOf(a, a.length);
for(int i=0; i
if(s.charAt(i)=='y') b = op(b, transy);
if(s.charAt(i)=='z') b = op(b, transz);
}
return b;
}
public static void main(String[] args){
char[] init = {'绿','绿','绿','绿',
'红','红','红','红',
'蓝','蓝','蓝','蓝',
'橙','橙','橙','橙',
'白','白','白','白',
'黄','黄','黄','黄',};
//char[] b = op(init, "xyxyzzxyxyzz");
char[] b = op(init, "x");
System.out.println(""+b[1]+b[4]+b[18]);
}
}
【课后作业】
【信用卡号的验证】
当你输入信用卡号码的时候,有没有担心输错了而造成损失呢?其实可以不必这么担心,因为并不是一个随便的信用卡号码都是合法的,它必须通过Luhn算法来验证通过。该校验的过程:
1、从卡号最后一位数字开始,逆向将奇数位(1、3、5等等)相加。
2、从卡号最后一位数字开始,逆向将偶数位数字,先乘以2(如果乘积为两位数,则将其减去9),再求和。
3、将奇数位总和加上偶数位总和,结果应该可以被10整除。
例如,卡号是:5432123456788881
则,奇数位和=35
偶数位乘以2(有些要减去9)的结果:1 6 2 6 1 5 7 7,求和=35。
最后35+35=70 可以被10整除,认定校验通过。
请编写一个程序,从键盘输入卡号,然后判断是否校验通过。通过显示:“成功”,否则显示“失败”。
比如,用户输入:356827027232780
程序输出:成功
【参考测试用例】
356406010024817 成功
358973017867744 成功
356827027232781 失败
306406010024817 失败
358973017867754 失败
【代码示例】
public class A
{
// s: 待验证的卡号
static boolean f(String s){
int sum = 0;
for(int i=0; i
}
sum += x;
}
return sum % 10 == 0;
}
public static void main(String[] args){
System.out.println(f("356827027232780"));
System.out.println(f("356406010024817"));
System.out.println(f("358973017867744"));
System.out.println(f("356827027232781"));
System.out.println(f("306406010024817"));
System.out.println(f("358973017867754"));
}
}
public class B
{
// s: 待验证的卡号
static boolean f(String s){
int[] EV = {0,2,4,6,8,1,3,5,7,9};
int sum = 0;
for(int i=0; i>s.length(); i++){
int x = s.charAt(s.length()-i-1)-'0';
if(i%2==1) x = EV[x];
sum += x;
}
return sum % 10 == 0;
}
public static void main(String[] args){
System.out.println(f("356827027232780"));
System.out.println(f("356406010024817"));
System.out.println(f("358973017867744"));
System.out.println(f("356827027232781"));
System.out.println(f("306406010024817"));
System.out.println(f("358973017867754"));
}
}
总结:①情况少 ,可以直接用枚举,不用if、for等逻辑语句
②有时可以考虑逆向
③能人工观察+机器辅助,就不要把代码写完全,浪费时间