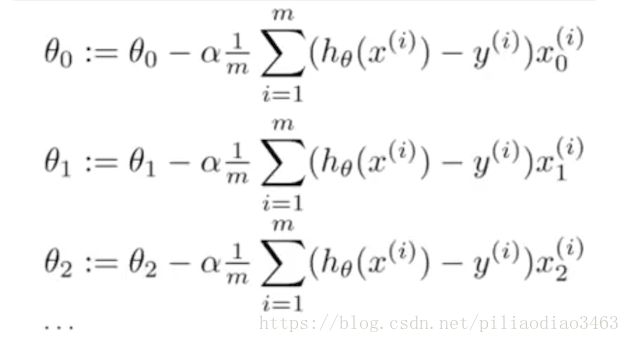学习笔记：机器学习--1.3多变量的梯度下降法

这是机器学习的第一章第三节：Gradient descent for Multiple variables(多变量的梯度下降法)

在学习本节过程中，将会涉及到高等数学中矩阵的相关知识

通过这一节的学习将会了解：

一、第一节中函数1.1.1，函数1.1.2和第二节中公式1.2.1在多个自变量\(x\)与多个parameter \(\theta_i\)的情况下的具体计算方法；

二、Feature Scaling(特征缩放) 和 Mean normalization(均值归一化) 的相关使用知识。

一、首先解释\(x_j^{(i)},y_j^{(i)},\theta_j\)(此时我们不再使用\(x_i,y_i\)，因为这时将会出现歧义)角标的含义，我们将其称为索引(index)。

我们还记得\(x\)表示的是自变量特征(features)，那么：

superscript \((i)\)相当于第\(i\)组数据(包含一条数据，所有特征。如果training set只有1组数据，那么此时将略去\(i\)不做讨论)，

subscript \(j\)相当于第\(j\)组特征(包含一组特征中的所有数据。如果只有1组特征，那么此时将略去\(j\)不做讨论)。

对于一般情况，通常存在\(m\)组数据，\(n\)个特征。我们可以通过下图进一步理解：

对于上图所示的数据组，不难发现一共有\(4\)个特征，此时由上述描述，可得：

\( x^{(2)}=\begin{bmatrix}1416\\3\\2\\40\end{bmatrix}\)，\(x_3^{(2)}=2\)。

因此，我们可以将features(特征\(x\)) 和parameters(参数\(\theta\))均用矩阵的形式表示如下：

\(x = \begin{bmatrix} x_0\\  x_1\\  \vdots\\  x_n\end{bmatrix},\;\theta = \begin{bmatrix} \theta_0\\  \theta_1\\  \vdots\\  \theta_n\end{bmatrix}\)，(对于\(x_0 = 1\)将在接下来的讨论中进行解释)

接下来我们对下面对三个函数公式进行分别讨论：

我们将函数1.1.1添加至\(n\)个特征，\(n+1\)个参数，结果如下：\(h_\theta(x) = \theta_0 + \theta_1x_1+\theta_2x_2+\cdots +\theta_n x_n\)

同时引入一个常数\(x_0^{(i)} = 1\)(带有角标\((i)\)表示对于任意一组数据，其\(x_0=1\)均成立)，函数1.1.1将变为：

\(h_\theta(x) = \theta_0x_0 + \theta_1x_1+\theta_2x_2+\cdots +\theta_n x_n\)，由于\(x_0^{(i)} = 1\)，将不影响函数计算结果。

此时根据矩阵运算，我们又可以将函数1.1.1写成如下形式：

\(h_\theta(x) = \begin{bmatrix} \theta_0 \ \theta_1\  \cdots\  \theta_n\end{bmatrix}\begin{bmatrix} x_0\\  x_1\\  \vdots\\  x_n\end{bmatrix} = \theta^Tx\)

此时我们可以认真对等式进行理解。同时需要注意，此时的features和parameters均有\(n+1\)项数据，表示为：

 \(x\in \mathbb{R}^{n+1}\;,\;\theta \in \mathbb{R}^{n+1}\)

同样对于函数1.1.2，由于parameters共有\(n+1\)个，因此将变为：

 \(\displaystyle J(\theta_0,\theta_1,\cdot,\theta_n)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x_i)-y_i)^2\)

将\((\theta_0,\theta_1,\cdot,\theta_n)\)用矩阵表示，又可将函数1.1.2写成如下形式：

\(\displaystyle J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x_i)-y_i)^2\)

接下来讨论公式1.2.1，其将变为：

\(\displaystyle \theta_j := \theta_j - \alpha\frac{\partial }{\partial \theta_j}J(\theta_0,\theta_1,\cdots,\theta_n)\)    \(j = 0,\cdots,n\)

将\((\theta_0,\theta_1,\cdots,\theta_n)\)用矩阵表示，也就是：

\(\displaystyle \theta_j := \theta_j - \alpha\frac{\partial }{\partial \theta_j}J(\theta)\)    (simultaneously update for every\(j = 0,\cdots,n\))

还记得当\(n=1\)时，我们需要同时更新\(\theta_0,\theta_1\)，计算形式如下：

可以发现，对于\(\theta_1\)的更新，其最后一项就是\(x_1^{(i)}\)，因此对于\(n>1\)的情况，其计算形式如下：

对应示例如下：

二、使用 Feature scaling(特征缩放) 和 Mean normalization(均值归一化) 这两个方法能够高效的进行梯度下降计算，从而降低计算\(min\,J(\theta)\)所需的循环次数，从而提高算法效率。

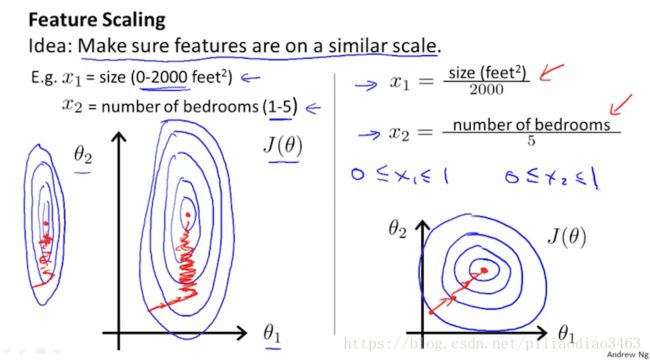
Feature scaling在课件中有如下描述：

Mean normalization在课件中这样描述：

如图片所示，Feature Scaling的要点在于将特征\(x_j\)缩放为一个在\(0\)到\(1\)之间的值，其具体计算方法是，对于\(x_j\)，若其范围是\(x_j\in (a,b)\)，则将\(x_j\)变为\(\frac{x_j}{b-a}\)(若范围值离散，如只能取整数，则分母为范围数)；

Mean normalization即是在Feature scaling的基础上，进一步将分子中的\(x_j\)减去其在training set(共\(m\)组数据)中的平均值，从而使整体的结果的均值更趋于\(0\)。

结合这两个方法，我们可以写出对于\(x_i\)的定义式，形式如下：

\(x_j^{(i)} := \frac{x_j^{(i)} - \mu_i}{s_i}\)

其中，\(\mu_i\)表示\(x_j^{(i)}\)的平均值，计算如下：\(\displaystyle \mu_i = \frac{1}{m}\sum_{i=1}^{m}x_j^{(i)}\)

\(s_i\)表示特征值的范围，计算如下：\(s_i = (max-min)\)

举一个简单的例子来说，如果\(x_1^{(i)}\)代表房价，且其范围\(x_1^{(i)} \in (100,2000)\)，房价平均值为\(1000\)，那么改进后的\(x_1^{(i)}\)表示如下：

\(x_1^{(i)} := \frac{x_1^{(i)} - \mu_i}{s_i}\)

end~