大数运算
大数运算(1)——大数存储
int (16位) -32768~32767
(注:现在大多数的编译器的int型是32位的 也就是说跟long型的大小一样)
long long或__int64(64位)
-9223372036854775808~9223372036854775807
float(32位) 精确到小数点后6~7位
double (64位) 精确到小数点后15~16位
(注:平时做题时 都把浮点型数据定义为double型 避免精度不够出错)
大数计算的数和结果精度一般是少则数十位,多则几万位。在C/C++语言中定义的类型中精度最多只有二十多位。一般我们称这种基本数据类型无法表示的整数为大整数。如何表示和存放大整数呢?基本的思想就是:用数组或字符串存放和表示大整数。一个数组或字符串元素,存放大整数中的一位。
例如:
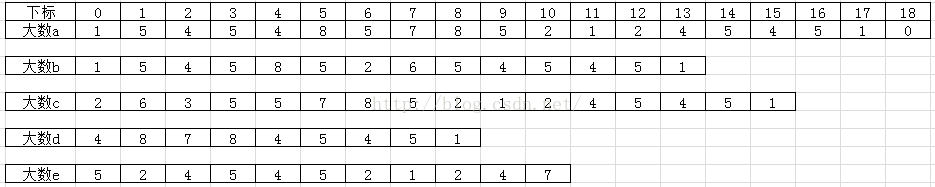
大数a:1545485785212454510
大数b:15458526545451
大数c:2635578521245451
大数d:487845451
大数e:52454521247
用字符串进行大数的储存后,若进行运算,可以根据ASCII表中字符串元素对应的ASCII值减去0的ASCII值进行运算。
例如:字符串中a[0]='4',其ASCII值是52,0的ASCII值是48,用52减去48正好是数字4。
大数运算(2)——大数加法
/*大数加法的中心思想就是:模拟人工列竖式算加法的方法。先从最低位开始相加,判断是否进1,一直到最高位。
例如:
求12545642233+278545的和,该怎么算?
是这样的:
3 3 2 2 4 6 5 4 5 2 1 0
+ 2 7 8 5 4 5 0 0 0 0 0 0
————————————————
5 //不进位,继续算下一位
0 //进位为1,并储存其各位数0
1 //2+8=10,10+1=11,同样,进位为1,并储存其各位数1
8 //不进位,继续算下一位
————————>
由低位向高位相加计算,注意判断是否进位!计算结束后,注意判断最后所得数组的长度,并去掉前导0。
下面是C语言代码实现:
#include
#include
int x[100]={0},y[100]={0},z[105]={0};//将数组元素全部初始化为0
int main()
{
char a[100],b[100];//通过字符串对大数进行输入并储存
int len1,len2,len;
while(scanf("%s %s",a,b))
{
int i,j=0,k=0;
len1=strlen(a);
len2=strlen(b);
for(i=len1-1;i>=0;i--)//将两个字符串中的字符转化为数字,并倒序储存到数组中,即字符串为123456,则数组为654321
{
x[j]=a[i]-'0';
j++;
}
for(i=len2-1;i>=0;i--)
{
y[k]=b[i]-'0';
k++;
}
if(len1>len2)
len=len1;
else
len=len2;
i=0;//从最低位(个位)开始进行计算
int m=0;
for(i=0;i=10)
m=1;
else
m=0;
}
if((x[i-1]+y[i-1]+m)>=10)//判断运算的最大位的和是否>=10
z[i]=1;
else
i=i-1;
for(;i>=0;i--)//到序输出数组
printf("%d",z[i]);
printf("\n");
}
return 0;
} 有时,你可能会遇到大数,但他是小数,例如125454521564564.56456132145645这样的,所以可以以小数点为界限,进行相加减。*/
大数运算(3)——大数减法
大数的减法与大数加法的方法有相似之处的,都是模拟人工运算的,从最低位开始运算,一直到最高位。
其方法是:
首先,要判断减数和被减数哪一个位数长,减数位数长是正常减;被减数位数长,则被减数减减数,最后还要加上负号;两数位数长度相等时,最好比较一下哪一个数字大,否则负号处理会很繁琐,用大的减去小的,最后加上负号;
其次,处理每一项时要,如果前一位相减有借位,就先减去上一位的借位,无则不减;再去判断是否能够减开被减数,如果减不开,就要借位后再去减,同时置借位为1,否则置借位为0。
结果可能会出现前面是一堆0的情况,要处理好,如当减数为112,而被减数为111时,会出现001 ,这时,需要将前面的0删除。
例如:13154-21213(同样,从最低位开始相减)
3 2 1 2 2
- 4 5 1 3 1
————————
9 //向前一位借1,则前一位的2变为1
6 // 2---->1向前一位借1,则前一位的1变为0
9 //1---->0向前一位借1,则前一位的2变为1
8 //2---->1向前一位借1,则前一位的2变为1
0 //不用借位。
9 6 9 8 0 //当然,输出时将0删除,并加上负号,即-9896
下面是C语言代码实现:
#include
#include
int x[100]={0},y[100]={0},z[105]={0};//将数组元素全部初始化为0
void sub(int x[],int y[],int len)
{
int i,j;
for(i=0;i=y[i])//如果x[i]>=y[i],不用向前一位借1,可直接减
z[i]=x[i]-y[i];
else //如果x[i]0;i--)//删除前缀0
{
if(z[i]==0)
len--;
else
break;
}
for(i=len-1;i>=0;i--) //倒序输出数组
printf("%d",z[i]);
printf("\n");
}
int main()
{
char a[100],b[100];//通过字符串对大数进行输入并储存
int len1,len2;
while(scanf("%s %s",a,b))
{
int i,j=0,k=0;
len1=strlen(a);
len2=strlen(b);
for(i=len1-1,j=0;i>=0;i--)//将两个字符串中的字符转化为数字,并倒序储存到数组中,即字符串为123456,则数组为654321
x[j++]=a[i]-'0';
for(i=len2-1,k=0;i>=0;i--)
y[k++]=b[i]-'0';
if(len1>len2) //若减数长度 > 被减数,正常减
sub(x,y,len1);
else if(len1=0;i--)//判断每一位两个数的大小
{
if(x[i]==y[i])
continue;
if(x[i]>y[i])//即减数大
{
sub(x,y,len1);
break;
}
if(x[i] 大数运算(4)——大数乘法
首先说一下乘法计算的算法:同样是模拟人工计算时的方法。
从低位向高位乘,在竖式计算中,我们是将乘数第一位与被乘数的每一位相乘,记录结果之后,用第二位相乘,记录结果并且左移一位,以此类推,直到计算完最后一位,再将各项结果相加,得出最后结果。
计算的过程基本上和小学生列竖式做乘法相同。为编程方便,并不急于处理进位,而将进位问题留待最后统一处理。
我们以125*53为例来说明计算过程:
1、先算125*3,3*5得到15个1,3*2得到6个10,3*1得到3个100;
![]()
2、接下来算125*5,5*5得到25个10,2*5得到10个100,5*1得到5个1000;
![]()
3、乘法过程完毕。接下来从 a[0]开始向高位逐位处理进位问题。a[0]留下5,把1 加到a[1]上,a[1]变为32 后,应留下2,把3 加到a[2]上……最终使得a里的每个元素都是1 位数,结果就算出来了
![]()
结果就是6625。
总结一个规律:即一个数的第i 位和另一个数的第j 位相乘所得的数,一定是要累加到结果的第i+j 位上。这里i, j 都是从右往左,从0 开始数。
即:ans[i+j] = a[i]*b[j];
另外进位时要处理,当前的值加上进位的值再看本位数字是否又有进位;前导清零。
下面是C语言代码实现:
#include
#include
#define MAX 100
char a[MAX],b[MAX];//用字符串进行数字的输入
int x[MAX+10],y[MAX+10],z[MAX*2+10];//积的位数最多是因数位数的两倍
int main()
{
int len1,len2,i,j;
while(~scanf("%s %s",a,b))
{
len1=strlen(a);
len2=strlen(b);
for(j=0,i=len1-1;i>=0;i--)//将字符串中字符转化为数字,并倒序储存
x[j++]=a[i]-'0';
for(j=0,i=len2-1;i>=0;i--)
y[j++]=b[i]-'0';
for(i=0;i=10) //若>=10
{
z[i+1]=z[i+1]+z[i]/10; //将十位上数字进位
z[i]=z[i]%10; //将个位上的数字留下
}
}
for(i=MAX*2;i>0;i--) //删除0的前缀
{
if(z[i]==0)
continue;
else
break;
}
for(;i>=0;i--) //倒序输出
printf("%d",z[i]);
printf("\n");
}
return 0;
} 大数运算(5)——大数除法(取模、取余)
有关于大数除法的运算可以大致分为两种:一种是求商(取模),另一种是求余数(取余)。
有两个大整数a和b,当a==b时,a/b==1,余数是0。(a!=0,b!=0)
当a>b时,a/b>=1,余数需要通过计算求得。
当a 而我们经常需要求的便是当a>b,这种情况我们该如何求商和余数呢? 其实基本的思想就是反复做减法,看看从被除数里最多能减去多少个除数,商就是多少。一个一个减显然太慢,如何减得更快一些呢? 以28536 除以23 为例来看一下:开始商为0。 先减去23 的1000 倍,就是23000,发现够减1 次,余下5536,于是商的值就增加1000; 然后用5536减去2300,发现够减2 次,余下936,于是商的值增加200,即1200; 再用936 减去230,够减4 次,余下16,于是商值增加40,即1240。 最后,发现余下的数比23小,即为余数,即28536 / 23 得1240余16。 这时,你会发现这其实就是咱们人工计算时相当于列的竖式。 另外,注意:我这里写的是有关大数除以大数的除法,同样适用于大数除以int类型范围的数,当然,也可以另写关于大数除以int的数。 这里写的全部是大整数,不包括小数。 下面是C语言代码实现: 第一种: lg(N!)=[lg(N*(N-1)*(N-2)*......*3*2*1)]+1 =[lgN+lg(N-1)+lg(N-2)+......+lg3+lg2+lg1]+1 用C语言实现: 第二种: 用Stirling公式计算n!结果的位数时,可以两边取对数, 得: log10(n!) = log10(2*PI*n)/2+n*log10(n/E); 对于大数来说,一个数的阶乘是非常大的,同样,一个int类型的整数,他的阶乘就有可能会很大。 就拿50来说,他的阶乘位数是65位,就已经远远超过了long long int类型的最大值。这时候,我们要通过字符串的方法,来进行阶乘的运算。 当然,需要注意的是: 我们所求一个数的阶乘,这个数是在int范围内的,5000的阶乘位数是16326位。 其方法是: 首先,我们是可以先求一定范围内的最大值的阶乘位数,以便于申请数组空间的确定。 对于大数问题,我们要有将大数与数组结合的思想,可以利用类似于人工求值的方法求出有关大数的问题。 对于大数阶乘来说,最重要的是如何将每个数的每位数与相对应的数组元素储存起来,就如算50的阶乘,我们要先从1开始乘: 1*2=2,将2存到a[0]中, 接下来是用a[0]*3; 2*3=6,将6储存在a[0]中, 接下来是用a[0]*4; 6*4=24,是两位数,那么24%10==4存到a[0]中,24/10==2存到a[1]中, 接下来是用a[0]*5;a[1]*5+num(如果前一位相乘结果位数是两位数,那么num就等于十位上的那个数字;如果是一位数,num==0) 24*5=120,是三位数,那么120%10==0存到a[0]中,120/10%10==2存到a[1]中,120/100==1存到a[2]中, 接下来是用a[0]*3;a[1]*6+num;a[2]*6+num; 120*6=720,那么720%10==0存到a[0]中,720/10%10==2存到a[1]中,720/100==7存到a[2]中, ................... 直到乘到50,将每一位数储存为止。 下面是C语言代码实现:#include大数运算(6)——大数阶乘(求位数)
#include
故n!的位数= log10(2*PI*n)/2+n*log10(n/E)+1(注意:当n=1时,算得的结果为0)
#include大数运算(7)——大数阶乘(求阶乘)
#include