J-linkage算法学习

原文：
【http://xueshu.baidu.com/s?wd=paperuri%3A%285cf06460732097a0248dce05c12126b0%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fwww.springerlink.com%2Fcontent%2Ff0310906x67884qv&ie=utf-8&sc_us=963783626136484965】
该算法的主要功能是拟合空间中的多个模型。多模型稳健估计。

一、论文解读
在introduction里提到了几种多模型估计的方法，简单说明一下。
1.RANSAC：原始的RANSAC是用于拟合数据中的单一模型的，后续提出的Sequential RANSAC可以用于拟合多个模型。Sequential RANSAC的主要思想是连续多次调用RANSAC，每次使用RANSAC拟合出一个模型之后，就将该模型确定的内点去掉，再使用RANSAC对剩余的点进行拟合。这种方法并不好，所以后续提出了multiple RANSAC[1]，如果模型之间不存在相交，那么该方法较为有效。但是该方法中，模型的数目需要人为指定，这在实际应用中并不方便。

另一种方法是随机霍夫变换（RHT）[2]，基于随机采样和投票，在参数空间内构造了一个直方图。随机选择一个最小样本集（MSS），其定义的唯一的模型的对应参数将会被存储到直方图内。直方图的峰值就对应着要找的模型。将其扩展到多模型也是很直观的：参数空间内的直方图的多个峰值。因此，RHT方法不需要事先知道模型的数目。但是，该方法受限于霍夫变换的经典缺陷，比如有限的精度以及较低的计算效率。同时，参数空间的选择和离散化至关重要。

[3]提出了一个用于估计多结构的算法，该算法基于个别点的残差分布的分析，这些个别点是与类RANSAC采样过程中产生的假设模型相关的。结果表明，残差分布的模式反映了模型的情况。该算法提出了一个新的视角：“与其研究每个假设模型的残差分布，不如去研究每个数据点的残差分布。”

每个数据点的残差都含有对应于真实模型的峰值，因为利用随机采样产生的假设模型会趋向于聚集在真实模型的附近，这也是RHT算法的基础。[3]中个提出的算法既能像RHT一样估计出模型的数目，又能做到像RANSAC一样高效。但是，我们的实验结果表明，搜索过程十分笨重。

基于RHT的思想和[3]中的算法，本文提出了J-linkage。但是和RHT的参数空间不同。

在对于数据中多个模型进行估计拟合的时候，噪声和离群点会产生很大的影响。本文基于随机采样和概念数据表示提出了该算法。对于数据中的每一个点，都采用与模型相关的特征函数来表示，那么，具有相同特征函数的点就可以之后利用J-linkage算法来进行聚类。该算法中，不需要指定模型的个数，参数调整也非必须。

算法概览：
首先进行随机采样。通过提取（draw）M个数据的最小集合，产生M个模型假设，这M个模型被称为最小样本集（MSS）。然后，每个模型的一致性集合（consensus set，CS，到该模型的距离小于一定阈值ε的点的集合）就可以计算出。【这边的逻辑我有点没搞清楚。既然已经得到了M个模型，难道不是通过对于点的聚类得到的吗？后面看下是否能解答】

构建一个NxM的矩阵，其中的每个元素e(i,j)表示点i和模型j的关系。如果i属于j，则e(i,j)置1，否则置0。该矩阵的每一列，对应于一个模型的一致性集合的特征函数（直译，我觉得应该是每一列对应于一个模型和数据中所有点的关系，属于该模型或不属于该模型）。每一行，反映了该点和哪个模型具有一致性，即该点属于哪个模型，也就是说，每一行表示的是一个点与所有模型的相关性，后面称之为某点的偏好集（preference set）。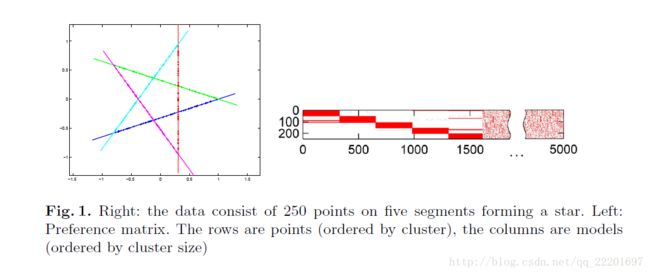

每个点的偏好集对应的特征函数实际上可以被看做该点的一个概念表示。属于同一个结构模型里的点应该具有相同的概念表示，换句话说，这些点应该聚集于（同样的）概念空间{0，1}^M。

2.1 随机采样
最小样本集（MSS）的构造是遵循下面的方式，即相邻的点具有更高的可能性被选中。也就是说，如果空间中一个点x_i已经被选中，那么点x_j被选中的概率遵循下面的计算法则：

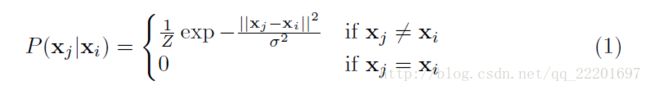
这里的Z是归一化系数，σ是试探地选出的。由上式看出，x_j和x_i相差越大，被选中的概率就越小。相等时，即为同一个点，也不会被选中。

然后，对于每一个点，它的偏好集就计算完成？？？？

由于论文写得很不清楚，下面从代码来学习该算法。

二、代码分析
代码的编写主要也是依据论文的结构来的。主要分为三个部分：
1.元素之间距离即采样概率的计算

[nearPtsTab] = calcNearPtsTab(log_oriP, 'exp', sigmaExp);

2.假设模型的生成（随机采样）

[totm, totd] = generateHypothesis(log_oriP, @getfn_plane, @distfn_plane, @degenfn_plane, 3, 4, 100,numberOfTrials, nearPtsTab);

3.利用J-linkage进行聚类

[T, Z, Y, totdbin] = clusterPoints(totd, inliersThreshold);

进入函数体分析。

第一个部分：元素之间距离即采样概率的计算。
这边利用的是指数分布，计算的是累计分布函数表，我有些不解。为什么要算累计分布？单纯两个元素（像素）之间的关系不就可以了吗？？？
进入函数[nearPtsTab] = calcNearPtsTab(log_oriP, 'exp', sigmaExp);
1）计算所有元素两两之间的欧几里得距离。K = pdist([Points]', 'euclidean');
2）将上一步得到的1*（N*（N-1）/2）的一维矢量转换成N*N的二维正方形矩阵。这边是很慢的，不可以直接计算得到该矩阵吗？为啥要分成两步。后面思考一下。
3）

[1]http://ieeexplore.ieee.org/abstract/document/1530351/
[2]http://xueshu.baidu.com/s?wd=paperuri%3A%28fbacdadbd62a80554389ba0d4150d31b%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fdl.acm.org%2Fcitation.cfm%3Fid%3D79420&ie=utf-8&sc_us=3656124035305645074
[3]http://xueshu.baidu.com/s?wd=paperuri%3A%2879c68d7d87d5b20e2f4e4ddd5f374339%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fsummary%3Fdoi%3D10.1.1.94.2093&ie=utf-8&sc_us=1531246600182632036