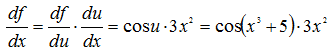【深度学习】神经网络(Neural Networks)基础之二——基于计算图理解神经网络的计算（前向传播，反向传播）

神经网络本质上就是一系列的 线性映射 与 非线性激活函数 交替组合而成的 复合运算。

神经网络的计算，都是按照前向传播（forward propagation）以及反向传播（back propagation）组织的【之所以叫做 “传播”，是因为计算其实就好比 “信号” 沿着一条 “管道”（pipeline）向前流动变化的过程】。

• 前向传播计算网络的输出
• 反向传播计算梯度，更新权重参数。

对于 复杂的，由多个函数组成的复合函数，我们可以利用 计算图（Computation Graph） 简单直观地表示其计算过程。

什么是计算图？

Computational Graph（计算图）

计算图是一种描述计算的 “语言”，它由节点（表示操作）和边（表示操作间流动的变量）组成。

用计算图描述计算

举个简单的例子，计算 $J=3(a+bc)$。

这个函数实际上可以 分解 成三个 基本计算：
$u=bc,v=a+u$ 和 $J=3v$。故可以 绘制成如下计算图的形式。

通过一个从左向右的过程（前向传播），我们可以计算出 $J$ 的值。

反过来，计算图上从右到左的过程（反向传播），便是用于计算导数最自然的方式。

反向传播

CS231n课程笔记翻译：反向传播笔记

反向传播是利用 链式法则 计算复合函数梯度的方法。

求导的链式法则 复合函数的导数等于其构成函数在相应点的导数的 乘积（微积分拾遗——链式法则），比如

$f(u)=sin(u)$

$u=x^3+5$

则

反向传播的具体做法

对于一个计算，在计算图中，每个门单元接受输入并计算两个东西：

1. 门单元的输出值
2. 输出值 关于 输入值 的 局部梯度。

门单元完成这两件事是完全独立的，即它不需要知道计算线路中的其他细节。

前向传播完毕，在反向传播的过程中，门单元将 回传的梯度 乘以 自身输出对于输入的局部梯度，从而获得 最终输出值 在 自己的输入值 上的梯度。

反向传播实战

假设有以下函数

这个函数是由多个门组成的。除了加法门，乘法门，还有下面这4种：

其中，sigmoid函数关于其输入的求导是可以简化的(使用了在分子上先加后减1的技巧)：

该神经元反向传播的代码实现如下：

w = [2,-3,-3] # 假设一些随机数据和权重
x = [-1, -2]

# 前向传播
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid函数

# 对神经元反向传播
ddot = (1 - f) * f # 点积变量的梯度, 使用sigmoid函数求导
dx = [w[0] * ddot, w[1] * ddot] # 回传到x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # 回传到w
# 完成！得到输入的梯度

反向传播的基本单元

在构建代码时创建了多个中间变量，每个都是比较简单的表达式，它们计算局部梯度的方法是已知的，这样计算反向传播就很简单了：

对于前向传播时产生每个变量(sigy, num, sigx, xpy, xpysqr, den, invden)进行回传，我们会有同样数量的变量，以d开头，用来存储对应变量的梯度。注意在反向传播的每一小块中都将包含了表达式的局部梯度，然后根据使用链式法则乘以上游梯度。对于每行代码，我们将指明其对应的是前向传播的哪部分。

# 回传 f = num * invden
dnum = invden # 分子的梯度                                         #(8)
dinvden = num                                                     #(8)
# 回传 invden = 1.0 / den 
dden = (-1.0 / (den**2)) * dinvden                                #(7)
# 回传 den = sigx + xpysqr
dsigx = (1) * dden                                                #(6)
dxpysqr = (1) * dden                                              #(6)
# 回传 xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# 回传 xpy = x + y
dx = (1) * dxpy                                                   #(4)
dy = (1) * dxpy                                                   #(4)
# 回传 sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # Notice += !! See notes below  #(3)
# 回传 num = x + sigy
dx += (1) * dnum                                                  #(2)
dsigy = (1) * dnum                                                #(2)
# 回传 sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy                                 #(1)

反向传播的注意细节：

1. 对前向传播变量进行缓存：在计算反向传播时，前向传播过程中得到的一些中间变量非常有用。在实际操作中，最好 对这些中间变量进行储存，这样在反向传播时可以直接使用，而不需要重新计算。
2. 在不同分支的梯度要相加：如果变量x，y在前向传播的表达式中出现多次，那么进行反向传播的时候就要非常小心，使用+=而不是=来累计这些变量的梯度（不然就会造成覆写）。这是遵循了在微积分中的多元链式法则，该法则指出如果变量在线路中分支走向不同的部分，那么 梯度在回传的时候，就应该进行累加。

---

神经网络的向量化计算

前向传播的向量化计算

以两层（一个隐藏层）神经网络为例。

其中，$x$表示输入特征，$a$表示每个神经元的输出，$W$表示特征的权重，上标 ${}^{[1]}$ 表示神经网络的层数（隐藏层为1），下标 ${}_1$ 表示该层的第几个神经元（神经网络的符号惯例）。

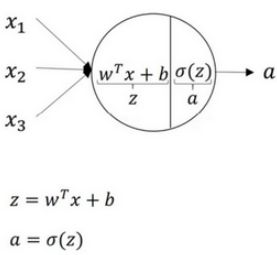
我们先简单考虑 单样本预测 的情况，从 单个神经元 开始。

一个神经元的计算分为两步，取隐藏层的第一个神经元为例：

1. 计算 $z_1^{[1]},z_1^{[1]}=w_1^{[1]T}x+b_1^{[1]}$。
2. 通过激活函数计算 $a_1^{[1]},a_1^{[1]}=\sigma (z_1^{[1]})$

隐藏层的第二个以及后面两个神经元的计算过程一样（一个神经网络，其实就只是进行了好多次重复的简单计算）。

$z_1^{[1]}=w_1^{[1]T}x+b_1^{[1]},a_1^{[1]}=\sigma (z_1^{[1]})$

$z_2^{[1]}=w_2^{[1]T}x+b_2^{[1]},a_2^{[1]}=\sigma (z_2^{[1]})$

$z_3^{[1]}=w_3^{[1]T}x+b_3^{[1]},a_3^{[1]}=\sigma (z_3^{[1]})$

$z_4^{[1]}=w_4^{[1]T}x+b_4^{[1]},a_4^{[1]}=\sigma (z_4^{[1]})$

向量化

下面我们将上述运算并行化向量化，依照以下规则：

• 竖直方向上，对应 一个网络层的不同节点。即竖直扫描，是索引到不同的隐藏单元。

我们 将样本的输入特征（$x_1,x_2$ 等） ，一层神经网络层的神经元参数 （$w_1^{[l]},w_2^{[l]}$ 等），线性映射值（$z_1,z_2$ 等）以及非线性激活值（$a_1,a_2$ 等）按行堆叠。


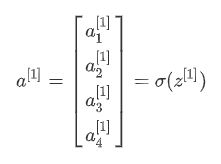
即每个神经网络层的 向量化计算公式 为，

$z^{[l]}=W^{[l]}{a}^{[l-1]}+b^{[l]}$（$x$可以看做$a^{[0]}$）

$a^{[l]}=g^{[l]}(z^{[l]})$

对于输入 $x$，可以表示为 $a^{[0]}$，对于网络最终的预测值 $\hat{y}$，$\hat{y}$ 即为最后一层的输出 $a^{[L]}$，其中 $L$ 表示网络的层数

多样本的向量化计算

我们通过多样本向量化，实现所有的训练样本同时进行计算，按照以下规则：

• 水平方向上，对应于 不同的样本。即水平扫描，是索引到不同的样本；

具体地，我们 将多个样本的输入（$x^{(1)},x^{(2)}$ 等），一层神经网络层对各个样本的线性映射值（$z_1^{(1)},z_2^{(2)}$ 等）以及非线性激活值（$a_1^{(1)},a_2^{(2)}$ 等）按列堆叠。

则每层神经网络层对多样本的向量化计算可以表示为大概下面这个样子

具体公式

$Z^{[l]}=W^{[l]}{A}^{[l-1]}+b^{[l]}$ ($X$ 可以看做 $A^{[0]}$ )

$A^{[l]}=\sigma (Z^{[l]})$

numpy代码

https://blog.csdn.net/u013733326/article/details/79702148

反向传播的向量化计算

http://www.ai-start.com/dl2017/html/lesson1-week3.html#header-n188

我们用一个简单例子来介绍神经网络反向传播的计算过程。

问题描述

使用一个单隐层神经网络来解决二分类任务。

网络参数有$W^{[1]},b^{[1]},W^{[2]},b^{[2]}$，$n_x$表示输入特征的个数，$n^{[1]}$表示隐藏单元个数，$n^{[2]}$表示输出单元个数。

我们使用二分交叉熵作为损失函数 loss function：

$L(\hat{y},y)=-ylog\hat{y}-(1-y)log(1-\hat{y})$

训练参数需要做梯度下降，每次梯度下降都会循环计算以下预测值：

$d{W}^{[1]}=\frac{dJ}{d{W}^{[1]}}$，$d{b}^{[1]}=\frac{dJ}{d{b}^{[1]}}$

$d{W}^{[2]}=\frac{dJ}{d{W}^{[2]}}$，$d{b}^{[2]}=\frac{dJ}{d{b}^{[2]}}$

然后基于梯度更新参数

$W^{[1]}⟹W^{[1]}-ad{W}^{[1]},b^{[1]}⟹b^{[1]}-ad{b}^{[1]}$

$W^{[2]}⟹W^{[2]}-\alpha \mathrm{d}{W}^{[2]},b^{[2]}⟹b^{[2]}-\alpha \mathrm{d}{b}^{[2]}$

则前向传播（forward propagation）方程如下：

(1) $Z^{[1]}=W^{[1]}X+b^{[1]}$

(2) $A^{[1]}=g^{[1]}(Z^{[1]})=\sigma (Z^{[n]})$

(3) $Z^{[2]}=W^{[2]}{A}^{[1]}+b^{[2]}$

(4) $[{\hat{y}}_1,{\hat{y}}_2,...,{\hat{y}}_m]=A^{[2]}=g^{[2]}(Z^{[2]})=\sigma (Z^{[2]})$

最终得到 loss function：

(5) $J(W^{[1]},b^{[1]},W^{[2]},b^{[2]})=\frac{1}{m}{\sum }_{i=1}^{m}L({\hat{y}}_i,y_i)=\frac{1}{m}{\sum }_{i=1}^m(-y_{i}log{\hat{y}}_i-(1-y_i)log(1-{\hat{y}}_i))$

根据前向传播倒推反向传播（back propagation）：

(1) $d{z}^{[2]}=A^{[2]}-Y,Y=\left[\begin{array}{cccc}{y}^{[1]}& y^{[2]}& \cdots & y^{[m]}\end{array}\right]$

(2) $d{W}^{[2]}=\frac{1}{m}d{z}^{[2]}{A}^{[1]T}$

(3) $\mathrm{d}{b}^{[2]}=\frac{1}{m}np.sum(d{z}^{[2]},axis=1,keepdims=True)$

(4) $d{z}^{[1]}=\underset{(n^{[1]},m)}{W^{[2]T}\mathrm{d}{z}^{[2]}}\ast \underset{activationfunctionofhiddenlayer}{{g^{[1]}}^{{}^{\prime }}}\ast \underset{(n^{[1]},m)}{(z^{[1]})}$

(5) $d{W}^{[1]}=\frac{1}{m}d{z}^{[1]}{x}^T$

(6) $\underset{(n^{[1]},1)}{d{b}^{[1]}}=\frac{1}{m}np.sum(d{z}^{[1]},axis=1,keepdims=True)$

关于反向传播的推导

吴恩达老师认为，反向传播的推导 是机器学习领域最难的数学推导之一，掌握不了其实也没大的关系，了解个大概就行，感兴趣的同学可以参考 这篇讲义。
（毕竟深度学习框架的反向传播操作可以自动进行的）

---

斯坦福 CS231n
吴恩达 deplearning.ai

神经网络(Neural Networks)基础系列笔记

【深度学习】神经网络(Neural Networks)基础之一——神经网络基本结构

【深度学习】神经网络(Neural Networks)基础之二——基于计算图理解神经网络的计算（前向传播，反向传播）