力扣高频|算法面试题汇总(十）：图论

力扣高频|算法面试题汇总(一）：开始之前
力扣高频|算法面试题汇总(二）：字符串
力扣高频|算法面试题汇总(三）：数组
力扣高频|算法面试题汇总(四）：堆、栈与队列
力扣高频|算法面试题汇总(五）：链表
力扣高频|算法面试题汇总(六）：哈希与映射
力扣高频|算法面试题汇总(七）：树
力扣高频|算法面试题汇总(八）：排序与检索
力扣高频|算法面试题汇总(九）：动态规划
力扣高频|算法面试题汇总(十）：图论
力扣高频|算法面试题汇总(十一）：数学&位运算

力扣高频|算法面试题汇总(十）：图论

力扣链接
目录：

• 1.单词接龙
• 2.岛屿数量
• 3.课程表
• 4.课程表 II

1.单词接龙

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典中的单词。
说明:
如果不存在这样的转换序列，返回 0。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的，且二者不相同。
示例 1:
输入:
beginWord = “hit”,
endWord = “cog”,
wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出: 5
解释: 一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”,
返回它的长度 5。

思路：
参考官方思路：广度优先搜索
用一个图来模拟整个流程，拥有一个 beginWord 和一个 endWord，分别表示图上的 start node 和 end node。中间节点是 wordList 给定的单词。对这个单词接龙每个步骤的唯一条件是相邻单词只可以改变一个字母。

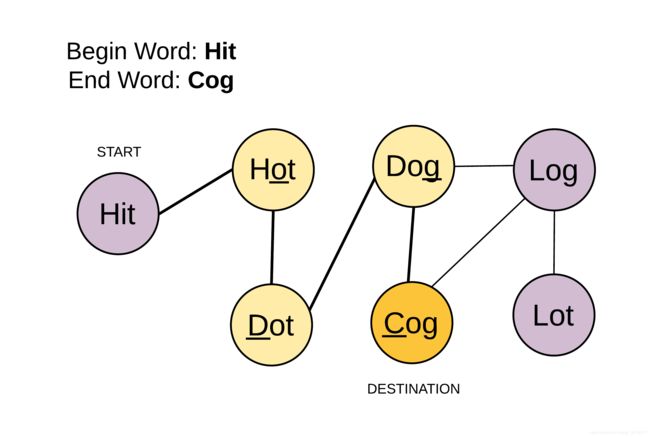
将问题抽象在一个无向无权图中，每个单词作为节点，差距只有一个字母的两个单词之间连一条边。问题变成找到从起点到终点的最短路径，如果存在的话。因此可以使用广度优先搜索方法。算法中最重要的步骤是找出相邻的节点，也就是只差一个字母的两个单词。为了快速的找到这些相邻节点，对给定的 wordList 做一个预处理，将单词中的某个字母用 * 代替

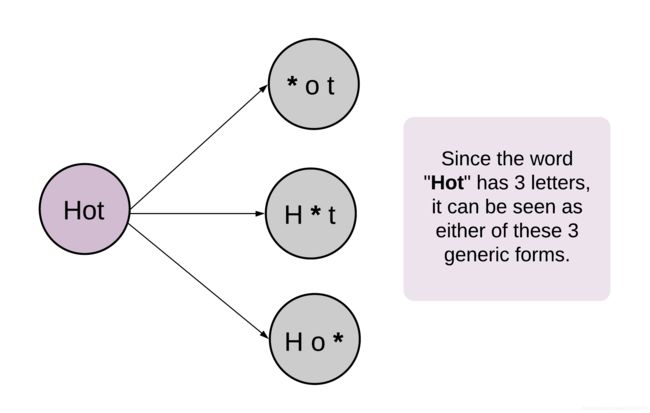
这个预处理构造了一个单词变换的通用状态。例如：Dog ----> D*g <---- Dig，Dog 和 Dig 都指向了一个通用状态 D*g。这步预处理找出了单词表中所有单词改变某个字母后的通用状态，并更方便也更快的找到相邻节点。否则，对于每个单词需要遍历整个字母表查看是否存在一个单词与它相差一个字母，这将花费很多时间。预处理操作在广度优先搜索之前高效的建立了邻接表。
在广搜时需要访问 Dug 的所有邻接点，可以先生成 Dug 的所有通用状态：

• 1.Dug => *ug
• 2.Dug => D*g
• 3.Dug => Du*

第二个变换 D*g 可以同时映射到 Dog 或者 Dig，因为他们都有相同的通用状态。拥有相同的通用状态意味着两个单词只相差一个字母，他们的节点是相连的。
算法步骤：

• 1.先对给定的wordList 进行预处理，将通用状态记录下来，键是通用状态，值是所有具有通用状态的单词。
• 2.将包含beginWord和1成对放入队列中，需要返回endWord 的层次也就是从beginWord 出发的最短距离。
• 3.使用visited记录访问的节点，避免重复访问，出现环。
• 4.当队列中有元素的时候，取出第一个元素，记为 current_word。
• 5.找到 current_word 的所有通用状态，并检查这些通用状态是否存在其它单词的映射，这一步通过检查 all_combo_dict 来实现。
• 6.从 all_combo_dict 获得的所有单词，都和 current_word 共有一个通用状态，所以都和 current_word 相连，因此将他们加入到队列中。
• 7.对于新获得的所有单词，向队列中加入元素 (word, level + 1) 其中 level 是 current_word 的层次。
• 8.最终到达期望的单词，对应的层次就是最短变换序列的长度。标准广度优先搜索的终止条件就是找到结束单词。

复杂度分析：
时间复杂度：$O(M\times N)$，其中 $M$ 是单词的长度 $N$ 是单词表中单词的总数。找到所有的变换需要对每个单词做 $M$ 次操作。同时，最坏情况下广度优先搜索也要访问所有的 $N$ 个单词。
空间复杂度：$O(M\times N)$，要在 all_combo_dict 字典中记录每个单词的 $M$ 个通用状态。访问数组的大小是 $N$。广搜队列最坏情况下需要存储 $N$ 个单词。

C++

class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        if(find(wordList.begin(), wordList.end(), endWord) == wordList.end()) return 0;
        // 可重复map 记录通用状态
        unordered_multimap<string, string> all_combo_dict;
        unordered_set<string> visited;
        for(auto word : wordList){
            string str = word;
            for(int i = 0; i < word.size(); ++i){
                str[i] = '*';
                all_combo_dict.emplace(str, word);
                str[i] = word[i];
            }
        }
        // 构造队列
        queue<string> wordQueue;
        wordQueue.push(beginWord); // 添加第一个元素
        int level = 1;
        while(!wordQueue.empty()){
            ++level;
            int length = wordQueue.size();
            while(length--){
                string cur = wordQueue.front(); // 获取队列中的第一个元素
                wordQueue.pop();
                for(int i = 0; i < cur.size(); ++i){
                    char tmp = cur[i];
                    cur[i] = '*'; // 修改成通用形式
                    // equal_range 返回范围[first,last)内等于指定值val的子范围的迭代器。
                    // 注意的是使用这个函数的前提是范围[first,last)内的元素是有序的。
                    // 同时注意函数的返回值类型，返回值是个pair对象，pair的first是左边界的迭代器，
                    // pair的second是右边界的迭代器。
                    // 区间是左闭右开的，[左边界，右边界)。
                    auto range = all_combo_dict.equal_range(cur);
                    for(auto itear = range.first; itear != range.second; ++itear){
                        if(visited.count(itear->second) == 0){ // 如果还没有访问
                            if(itear->second == endWord) return level; // 如果找到，返回结果
                            wordQueue.push(itear->second);
                            visited.emplace(itear->second);
                        }
                    }
                    cur[i] = tmp; // 还原
                }
            }
        }
        return 0;
    }
};

Python

# defaultdict构造有默认输出的字典
from collections import defaultdict
class Solution(object):
    def ladderLength(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: int
        """
        if not endWord in wordList or not beginWord or not endWord or not wordList:
            return 0
        # 获取单词的长度
        length = len(beginWord)
        # 字典用来存放任何给定单词的组合词。一次换一个字母
        all_combo_dict = defaultdict(list)
        for word in wordList:
            for i in range(length):
                # 键是通用词
                # 值是具有相同中间泛型单词的单词列表
                all_combo_dict[word[:i] + "*" + word[i+1:]].append(word)
        # 队列BFS
        queue = [(beginWord, 1)]
        # Visited以确保不会重复处理相同的字
        visited = {beginWord: True}
        while queue:
            current_word, level = queue.pop(0)
            for i in range(length):
                # 现在词的中间词
                intermediate_word = current_word[:i] + "*" + current_word[i+1:]
                # 下一个状态是所有中间状态相同的词。
                for word in all_combo_dict[intermediate_word]:
                    # 如果在任何时候，如果找到要找的东西，即结束词，可以返回答案。
                    if word == endWord:
                        return level + 1
                    # 否则，将其添加到BFS队列。也标志着它访问
                    if word not in visited:
                        visited[word] = True
                        queue.append((word, level + 1))
                all_combo_dict[intermediate_word] = [] # 有visited 这个可以不加
        return 0             

思路2：
参考官方思路：双向广度优先搜索
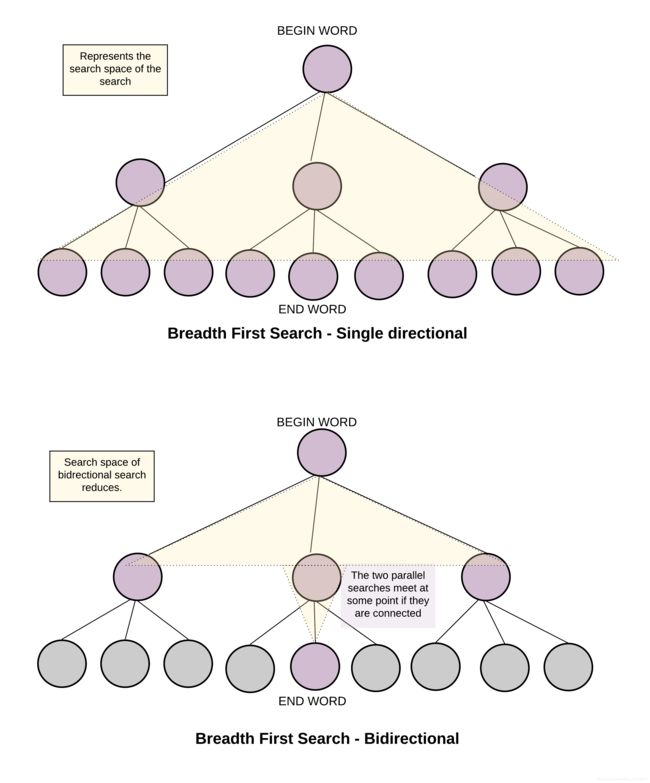
在思路1中，根据给定字典构造的图可能会很大，而广度优先搜索的搜索空间大小依赖于每层节点的分支数量。假如每个节点的分支数量相同，搜索空间会随着层数的增长指数级的增加。
如果使用两个同时进行的广搜可以有效地减少搜索空间。一边从 beginWord 开始，另一边从 endWord 开始。每次从两边各扩展一个节点，当发现某一时刻两边都访问了某一顶点时就停止搜索。这就是双向广度优先搜索，它可以可观地减少搜索空间大小，从而降低时间和空间复杂度。

算法步骤：

• 1.算法核心和思路1相似，不过从两个节点同时开始搜索，同时搜素的结束条件也有所变化。
• 2.使用两个访问数组，分别记录从对应的起点是否已经访问了该节点。
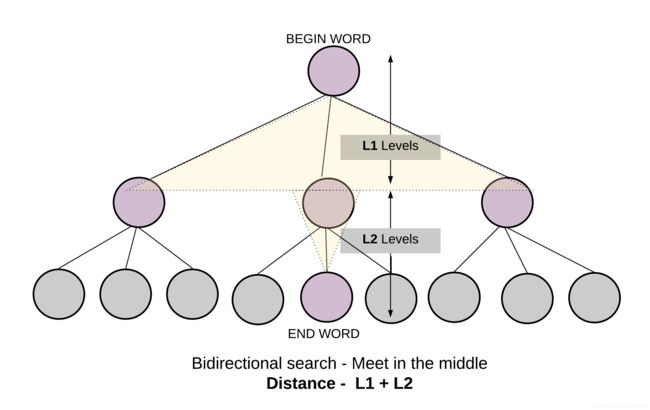
• 3.如果发现一个节点被两个搜索同时访问，就结束搜索过程。因为找到了双向搜索的交点。过程如同从中间相遇而不是沿着搜索路径一直走。双向搜索的结束条件是找到一个单词被两边搜索都访问过了。
• 4.最短变换序列的长度就是中间节点在两边的层次之和。因此可以在访问数组中记录节点的层次。
  
  复杂度分析：

时间复杂度：$O(M\times N)$，其中 $M$ 是单词的长度 $N$ 是单词表中单词的总数。找到所有的变换需要对每个单词做 $M$ 次操作。但是搜索时间会被缩小一半，因为两个搜索会在中间某处相遇。
空间复杂度：$O(M\times N)$，要在 all_combo_dict 字典中记录每个单词的 $M$ 个通用状态。访问数组的大小是 $N$。但是因为会在中间相遇，所以双向搜索的搜索空间变小。
C++

class Solution {
public:
    unordered_map<string, vector<string>> all_combo_dict;
    int length;
    int visitWordNode(queue<pair<string, int>>& que,
                      unordered_map<string, int>& visited,
                      unordered_map<string, int>& others_visited){
        string current_word = que.front().first;
        int level = que.front().second;
        que.pop();
        for(int i = 0; i < length; ++i){
            string index = current_word.substr(0, i)+"*"+current_word.substr(i+1, length);
            for(auto str : all_combo_dict[index]){
                if(others_visited[str])
                    return level + others_visited[str];
                if(!visited[str]){
                    que.push(make_pair(str, level+1));
                    visited[str] = level + 1;
                }
            }
        }
        return -1;
    }
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        if(find(wordList.begin(), wordList.end(), endWord) == wordList.end()) return 0;
        unordered_set<string> visited;
        for(auto word : wordList){ /*构造通用字典*/
            string str = word;
            for(int i = 0; i < word.size(); ++i){
                str[i] = '*';
                all_combo_dict[str].push_back(word);
                str[i] = word[i];
            }
        }
        length = beginWord.size();
        // 构造双向BFS队列
        queue<pair<string, int>> queue_beginWord; // BFS从beginWord开始
        queue_beginWord.push(make_pair(beginWord, 1));
        queue<pair<string, int>> queue_endWord;   // BFS从endWord开始
        queue_endWord.push(make_pair(endWord, 1));
        // visited标志，确保不会重复处理相同的字
        unordered_map<string, int> visited_begin;
        unordered_map<string, int> visited_end;
        visited_begin[beginWord] = 1;
        visited_end[endWord] = 1;
        int res;
        // 做一个双向搜索，从BFS从beginWord开始开始一个指针，
        // 从endWord开始一个指针。一个接一个地跳。
        while(!queue_beginWord.empty() && !queue_endWord.empty()){
            res = visitWordNode(queue_beginWord, visited_begin, visited_end);
            if(res != -1) return res;
            res = visitWordNode(queue_endWord, visited_end, visited_begin);
            if(res != -1) return res;
        }
        return 0;
    }
};

Python

# defaultdict构造有默认输出的字典
from collections import defaultdict
class Solution(object):
    # 初始化
    def __init__(self):
        self.length = 0 # 每个单词的长度
        # 字典用来存放任何给定单词的组合词。一次换一个字母。
        self.all_combo_dict = defaultdict(list)
    def ladderLength(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: int
        """ 
        if not endWord in wordList: return 0
        self.length = len(beginWord) # 因为所有单词的长度都是一样的。
        # 构建字典
        for word in wordList:
            for i in range(self.length):
                # 键是通用词
                # 值是具有相同中间泛型单词的单词列表
                self.all_combo_dict[word[:i] + '*' + word[i+1:]].append(word)
        # 双向BFS队列
        queue_begin = [(beginWord, 1)] # BFS从beginWord开始
        queue_end = [(endWord, 1)] # BFS从endWord开始
        # 访问标志，以确保不会重复处理相同的字
        visited_begin = {beginWord: 1}
        visited_end = {endWord: 1}
        ans = None
        # 做一个双向搜索，从BFS从beginWord开始开始一个指针，
        # 从endWord开始一个指针。一个接一个地跳。
        while queue_begin and queue_end:
            # 从begin word 开始
            ans = self.visitWordNode(queue_begin, visited_begin, visited_end)
            if ans:
                return ans
            # 从end word 开始
            ans = self.visitWordNode(queue_end, visited_end, visited_begin)
            if ans:
                return ans
            
        return 0
    def visitWordNode(self, queue, visited, other_visited):
        current_word, level = queue.pop(0)
        for i in range(self.length):
            # 现在词的中间词
            intermediate_word = current_word[:i] + "*" + current_word[i+1:] 
            # 下一个状态是所有中间状态相同的词。
            for word in self.all_combo_dict[intermediate_word]:
                # 如果中间状态/单词已经从另一个并行遍历访问过，这意味着找到了答案。
                if word in other_visited:
                    return level + other_visited[word]
                if word not in visited:
                    # 将level另存为字典的值，以节省跃点数。
                    visited[word] = level + 1
                    queue.append((word, level + 1))
        return None             

2.岛屿数量

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。
此外，你可以假设该网格的四条边均被水包围。
示例 :
输入:
11000
11000
00100
00011
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。

思路：
参考官方思路，深度优先遍历。
总结一下：

• 1.将二维网格看成一个无向图，竖直或水平相邻的 1之间有边相连。
• 2.扫面整个网络，如果网格值为1，则以此为起点进行深度优先遍历(上下左右)，并将遍历过的网格的值赋值为0。
• 3.有多少次遍历，就有多少个岛屿。

参考图示：

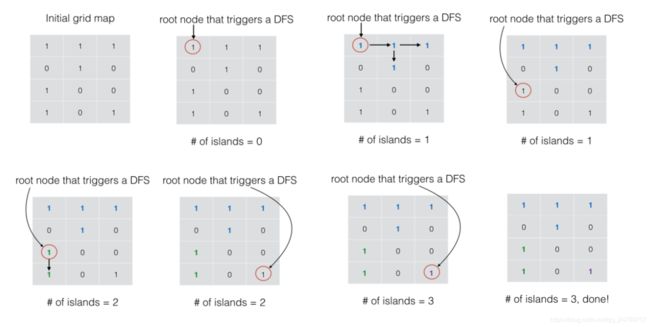
复杂度分析：
时间复杂度：$O(MN)$，其中 $M$ 和 $N$ 分别为行数和列数。
空间复杂度：$O(MN)$，在最坏情况下，整个网格均为陆地，深度优先搜索的深度达到 $MN$。

C++

class Solution {
public:
    void dfs(vector<vector<char>>& grid, int row, int col){
        int n_row = grid.size();
        int n_col = grid[0].size();

        // 先清0
        grid[row][col] = '0';
        // dfs遍历上下左右
        if(row - 1 >= 0 && grid[row-1][col] == '1') dfs(grid, row - 1, col);
        if(row + 1 < n_row && grid[row+1][col] == '1') dfs(grid, row + 1, col);
        if(col - 1 >= 0 && grid[row][col-1] == '1') dfs(grid, row, col - 1);
        if(col + 1 < n_col && grid[row][col+1] == '1') dfs(grid, row, col + 1);

    }
    int numIslands(vector<vector<char>>& grid) {
        int n_row = grid.size(); // 获取行数
        if(!n_row) return 0;
        int n_col = grid[0].size(); // 获取列数

        int num_islands = 0; // 岛屿数
        for(int row = 0; row < n_row; ++row){
            for(int col = 0; col < n_col; ++col)
                if(grid[row][col] == '1'){
                    ++num_islands; // 岛屿数加1
                    dfs(grid, row, col); // dfs遍历，把1变0
                }
        }
        return num_islands;
    }
};

Python：

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        n_row = len(grid)
        if n_row == 0: return 0
        n_col = len(grid[0])
        
        num_islands = 0
        for row in range(n_row):
            for col in range(n_col):
                if grid[row][col] == '1':
                    num_islands += 1
                    self.dfs(grid, row, col)
        return num_islands
    def dfs(self, grid, row, col):
        n_row = len(grid)
        n_col = len(grid[0])
        
        grid[row][col] = '0'
        if row - 1 >= 0 and grid[row-1][col] == '1': self.dfs(grid, row-1, col)
        if row + 1 < n_row and grid[row+1][col] == '1': self.dfs(grid, row+1, col)
        if col - 1 >= 0 and grid[row][col-1] == '1': self.dfs(grid, row, col-1)
        if col + 1 < n_col and grid[row][col+1] == '1': self.dfs(grid, row, col+1)

思路2：
参考官方思路，广度优先遍历。

和深度优先遍历类似，只不过把遍历方式转换成了广度优先遍历，遍历过的位置，会把1变成0。有多少次遍历，就有多少个岛屿。
复杂度分析
时间复杂度：$O(MN)$，其中 $M$ 和 $N$ 分别为行数和列数。
空间复杂度: $O(min(M,N))$，在最坏情况下，整个网格均为陆地，队列的大小可以达到 $min(M,N)$。

C++

class Solution {
public:

    int numIslands(vector<vector<char>>& grid) {
        int n_row = grid.size(); // 获取行数
        if(!n_row) return 0;
        int n_col = grid[0].size(); // 获取列数

        int num_islands = 0; // 岛屿数
        // 使用bfs搜素
        for(int row = 0; row < n_row; ++row){
            for(int col = 0; col < n_col; ++col){
                if(grid[row][col] == '1'){
                    ++num_islands;
                    grid[row][col] = '0';
                    // 新建队列进行广度搜素
                    queue<pair<int, int>> neighbors;
                    neighbors.push(make_pair(row, col));
                    while(!neighbors.empty()){
                        auto row_col = neighbors.front(); // 获取队列的第一个元素
                        neighbors.pop();
                        int cur_row = row_col.first;
                        int cur_col = row_col.second;
                        // 四个方向
                        if(cur_row - 1 >= 0 && grid[cur_row-1][cur_col] == '1'){
                            neighbors.push(make_pair(cur_row-1, cur_col));
                            grid[cur_row-1][cur_col] = '0';
                        }
                        if(cur_row + 1 < n_row && grid[cur_row+1][cur_col] == '1'){
                            neighbors.push(make_pair(cur_row+1, cur_col));
                            grid[cur_row+1][cur_col] = '0';                        
                        }
                        if(cur_col - 1 >= 0 && grid[cur_row][cur_col-1] == '1'){
                            neighbors.push(make_pair(cur_row, cur_col-1));
                            grid[cur_row][cur_col-1] = '0';                          
                        }
                        if(cur_col + 1 < n_col && grid[cur_row][cur_col+1] == '1'){
                            neighbors.push(make_pair(cur_row, cur_col+1));
                            grid[cur_row][cur_col+1] = '0';                          
                        }
                    }
                }

            }
        }
        return num_islands;
    }
};

Python:

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        n_row = len(grid)
        if n_row == 0: return 0
        n_col = len(grid[0])
        
        num_islands = 0
        for row in range(n_row):
            for col in range(n_col):
                if grid[row][col] == '1':
                    num_islands += 1
                    grid[row][col] = "0"
                    neighbors = collections.deque([(row, col)])
                    while neighbors:
                        cur_row, cur_col = neighbors.popleft() # 将最左边的元素取出
                        for x, y in [(cur_row-1, cur_col), (cur_row+1, cur_col), (cur_row, cur_col-1), (cur_row, cur_col+1)]:
                            if 0<=x<n_row and 0<=y<n_col and grid[x][y] == '1':
                                neighbors.append((x, y))
                                grid[x][y] = '0'                  
        return num_islands

3.课程表

你这个学期必须选修 numCourse 门课程，记为 0 到 numCourse-1 。
在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，用一个匹配来表示他们：[0,1]
给定课程总量以及它们的先决条件，请你判断是否可能完成所有课程的学习？
示例 1:
输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。
提示：
输入的先决条件是由 边缘列表 表示的图形，而不是 邻接矩阵 。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
1 <= numCourses <= 10^5

思路：
参考讲解：入度表(广度优先遍历)
首先本题可以转化为：课程安排图是否是有向无环图(DAG)。即课程间规定了前置条件，但不能构成任何环路，否则课程前置条件将不成立。通过 拓扑排序 判断此课程安排图是否是 有向无环图(DAG) 。通过题目条件numCourses，构建邻接表，以降低算法时间复杂度。
算法步骤：
1.构建邻接表adjList，以及记录每个节点的入度indegrees。
2.创建一个队列，把所有入度为0的节点入队。
3.进行BFS 拓扑排序: 将此节点对应的所有节点的入度-1，即indegrees[cur] -= 1，如果减一之后，对应的节点的入度为0，说明 cur 所有的前驱节点已经被 “删除”，则放入队列中。
4.在每次 pre 出队时，执行 numCourses--；若整个课程安排图是有向无环图（即可以安排），则所有节点一定都入队并出队过，即完成拓扑排序。换个角度说，若课程安排图中存在环，一定有节点的入度始终不为 0。因此，拓扑排序出队次数等于课程个数，返回 numCourses == 0 判断课程是否可以成功安排。、
参考图示：

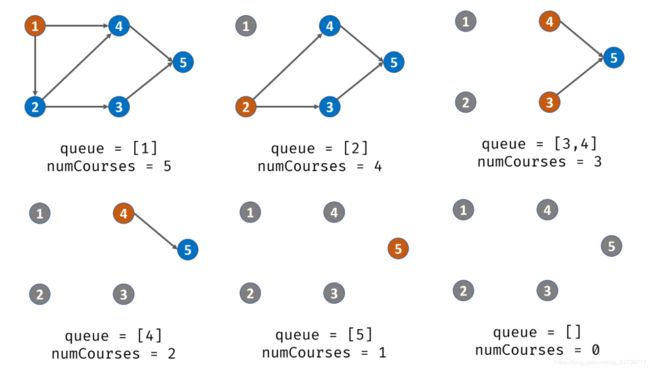
复杂度分析：
时间复杂度 $O(N+M)$： 遍历一个图需要访问所有节点和所有临边，$N$ 和 $M$ 分别为节点数量和临边数量；
空间复杂度 $O(N+M)$： 为建立邻接表所需额外空间，adjList 长度为 $N$，并存储 $M$ 条临边的数据。

C++

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<int> indegrees(numCourses);
        vector<vector<int>> adjList(numCourses);
        queue<int> nodes;
        // 获得每门课程入度和邻接表
        for(int i = 0; i < prerequisites.size(); ++i){
            ++indegrees[prerequisites[i][0]];
            adjList[prerequisites[i][1]].push_back(prerequisites[i][0]);
        }
        // 获得所有入度为0的课程
        for(int i = 0; i < numCourses; ++i){
            if(indegrees[i] == 0)
                nodes.push(i);
        }
        // BFS 拓扑排序
        while(!nodes.empty()){
            int pre = nodes.front();
            nodes.pop();
            --numCourses;
            for(int i = 0; i < adjList[pre].size(); ++i){
                --indegrees[adjList[pre][i]];
                if(indegrees[adjList[pre][i]] == 0) nodes.push(adjList[pre][i]);
            }
        }
        return numCourses == 0;
    }
};

Python

from collections import deque
class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        indegrees = [0 for _ in range(numCourses)] # 给每个节点分配入度
        adjList = [[] for _ in range(numCourses)]  # 构建邻接表
        queue = deque() # 新建队列
        # 获得每门课程入度和邻接表
        for cur, pre in prerequisites:
            indegrees[cur] += 1
            adjList[pre].append(cur)
        # 获得所有入度为0的课程    
        for i in range(numCourses):
            if indegrees[i] == 0: queue.append(i)
        # BFS 拓扑排序
        while queue:
            pre = queue.popleft() # 将最左边的元素取出
            numCourses -= 1       # 课程数量减一
            for cur in adjList[pre]: # 获取链接pre的所有节点
                indegrees[cur] -= 1  # 入度减一
                if indegrees[cur] == 0: queue.append(cur) # 如果入度为0，则加入队列
        
        return numCourses == 0

思路2：
参考讲解：深度优先遍历
1.借助一个标志列表 flags，用于判断每个节点 i （课程）的状态：

• 未被 DFS 访问：i == 0；
• 已被其他节点启动的 DFS 访问：i == -1；
• 已被当前节点启动的 DFS 访问：i == 1。

2.对 numCourses 个节点依次执行 DFS，判断每个节点起步 DFS 是否存在环，若存在环直接返回 False。DFS 流程；

• 终止条件：
  当 flag[i] == -1，说明当前访问节点已被其他节点启动的 DFS 访问，无需再重复搜索，直接返回 True。
  当 flag[i] == 1，说明在本轮 DFS 搜索中节点 i 被第 22 次访问，即 课程安排图有环 ，直接返回False。
• 将当前访问节点 i 对应 flag[i] 置 1，即标记其被本轮 DFS 访问过；
• 递归访问当前节点 i 的所有邻接节点 j，当发现环直接返回 False；
• 当前节点所有邻接节点已被遍历，并没有发现环，则将当前节点 flag 置为 -1并返回 True。

3.若整个图 DFS 结束并未发现环，返回 True。

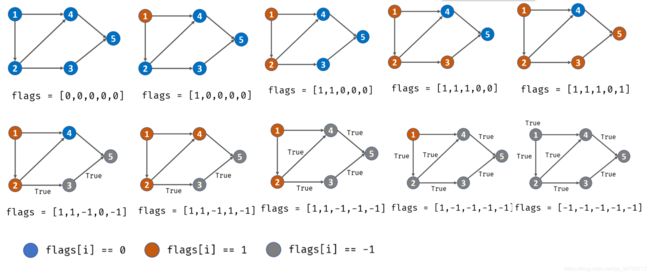
C++

class Solution {
public:
    bool dfs(int idNode, vector<vector<int>>& adjList, vector<int>& flags){
        if(flags[idNode] == 1) return false;
        if(flags[idNode] == -1) return true;
        flags[idNode] = 1;
        for(int i = 0; i < adjList[idNode].size(); ++i)
            if(!dfs(adjList[idNode][i], adjList, flags)) return false;
        flags[idNode] = -1;
        return true;
    }
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<int> flags(numCourses);
        vector<vector<int>> adjList(numCourses);
        for(int i = 0; i < prerequisites.size(); ++i){
            adjList[prerequisites[i][1]].push_back(prerequisites[i][0]);
        }
        for(int i = 0; i < numCourses; ++i){
            if(!dfs(i, adjList, flags)) return false;
        }
        return true;
    }
};

Python

from collections import deque
class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        def dfs(idNode, adjList, flags):
            # 在本轮 DFS 搜索中节点 i 被第 2次访问，即 课程安排图有环 
            if flags[idNode] == 1: return False
            # 当前访问节点已被其他节点启动的 DFS 访问，无需再重复搜索
            if flags[idNode] == -1: return True
            flags[idNode] = 1 # 已被当前节点启动的 DFS 访问
            for nextNode in adjList[idNode]:
                if not dfs(nextNode, adjList, flags): return False
            flags[idNode] = -1 # 记为-1，避免重复搜索
            
            return True
            
        adjList = [[] for _ in range(numCourses)] # 构建邻接表
        flags = [0 for _ in range(numCourses)]  # 访问标志
        for cur, pre in prerequisites:
            adjList[pre].append(cur) # 创建邻接表
        for i in range(numCourses): # 从0 ~ numCourses-1 出发遍历
            if not dfs(i, adjList, flags): return False
        return True

4.课程表 II

现在你总共有 n 门课需要选，记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。
示例 :
输入: 4, [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
说明:
输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
提示:
这个问题相当于查找一个循环是否存在于有向图中。如果存在循环，则不存在拓扑排序，因此不可能选取所有课程进行学习。
通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程（21分钟），介绍拓扑排序的基本概念。
拓扑排序也可以通过 BFS 完成。

思路：
参考官方思路:深度优先搜索。
可以将本题建模成一个求拓扑排序的问题了：

• 将每一门课看成一个节点；
• 如果想要学习课程 A 之前必须完成课程 B，那么从 B 到 A 连接一条有向边。这样以来，在拓扑排序中，B 一定出现在 A的前面。

可以将深度优先搜索的流程与拓扑排序的求解联系起来，用一个栈来存储所有已经搜索完成的节点。
对于一个节点 u，如果它的所有相邻节点都已经搜索完成，那么在搜索回溯到 u的时候，u本身也会变成一个已经搜索完成的节点。这里的「相邻节点」指的是从 u 出发通过一条有向边可以到达的所有节点。
算法步骤：
对于图中的任意一个节点，它在搜索的过程中有三种状态，即：

• 未搜索：还没有搜索到这个节点；
• 搜索中：搜索过这个节点，但还没有回溯到该节点，即该节点还没有入栈，还有相邻的节点没有搜索完成）；
• 已完成：搜索过并且回溯过这个节点，即该节点已经入栈，并且所有该节点的相邻节点都出现在栈的更底部的位置，满足拓扑排序的要求

通过上述的三种状态，可以给出使用深度优先搜索得到拓扑排序的算法流程，在每一轮的搜索搜索开始时，任取一个未搜索的节点开始进行深度优先搜索。
将当前搜索的节点 u 标记为搜索中，遍历该节点的每一个相邻节点 v：

• 如果 v 为未搜索，那么开始搜索 v，待搜索完成回溯到 u；
• 如果 v 为搜索中，那么就找到了图中的一个环，因此是不存在拓扑排序的；
• 如果 v为已完成，那么说明 v 已经在栈中了，而 u还不在栈中，因此 u 无论何时入栈都不会影响到 (u, v)之前的拓扑关系，以及不用进行任何操作

u 的所有相邻节点都为已完成时，将 u 放入栈中，并将其标记为已完成。
在整个深度优先搜索的过程结束后，如果没有找到图中的环，那么栈中存储这所有的 nn 个节点，从栈顶到栈底的顺序即为一种拓扑排序。参考图示：图中的「白色」「黄色」「绿色」节点分别表示「未搜索」「搜索中」「已完成」的状态。



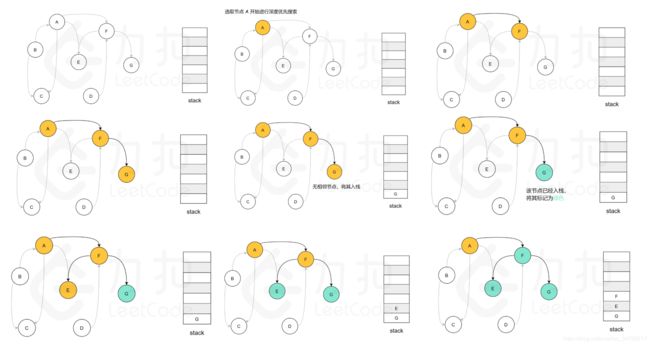
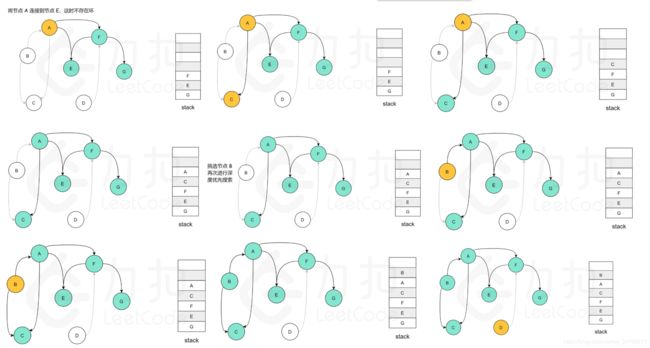
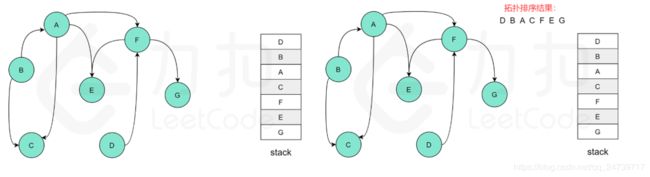
复杂度分析:
时间复杂度: $O(n+m)$，其中 $n$为课程数，$m$ 为先修课程的要求数。这其实就是对图进行深度优先搜索的时间复杂度。
空间复杂度: $O(n+m)$。题目中是以列表形式给出的先修课程关系，为了对图进行深度优先搜索，需要存储成邻接表的形式，空间复杂度为 $O(m)$。在深度优先搜索的过程中，需要最多 $O(n)$ 的栈空间（递归）进行深度优先搜索，并且还需要若干个 $O(n)$的空间存储节点状态、最终答案等。

C++

class Solution {
private:
    vector<vector<int>> edges; /*存储有向图的每一条边*/
    vector<int> visited; /*存储每个节点的访问状态， 0=未搜索，1=搜索中，2=已完成*/
    vector<int> res; /*用数组来模拟栈，下标0为栈底*/
    bool invalid; /*判断有向图中是否有环*/
public:
    void dfs(int node){
        visited[node] = 1;/*将节点标记为 搜索中*/
        // 搜索其相邻节点
        // 只要发现有环，立刻停止搜索
        for(int v : edges[node]){
            // 如果「未搜索」那么搜索相邻节点
            if(visited[v] == 0){
                dfs(v);
                if(invalid) return;
            }// 如果「搜索中」说明找到了环
            else if(visited[v] == 1){
                invalid = true;
                return;
            }           
        }
        // 将节点标记为「已完成」
        visited[node] = 2;
        // 将节点入栈
        res.push_back(node);
    }
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        edges.resize(numCourses); /*初始化*/
        visited.resize(numCourses);
        // 创建有向图
        for (const auto& info: prerequisites) {
            edges[info[1]].push_back(info[0]);
        }
        // 每次挑选一个 未搜索 的节点，开始进行深度优先搜索
        for(int i = 0; i < numCourses && !invalid; ++i){
            if(!visited[i]) dfs(i); /*如果还未访问，则进行深度优先遍历*/
        }
        if(invalid) return {}; /*如果有环，则返回空列表*/
        // 如果没有环，那么就有拓扑排序
        // 注意下标 0 为栈底，因此需要将数组反序输出
        reverse(res.begin(), res.end());
        return res;
    }
};

Python

class Solution:
    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        # 存储有向图
        edges = collections.defaultdict(list)
        # 标记每个节点的状态：0=未搜索，1=搜索中，2=已完成
        visited = [0] * numCourses
        # 用数组来模拟栈，下标 0 为栈底，n-1 为栈顶
        res = list()
        # 判断有向图中是否有环
        invalid = False
        
        for info in prerequisites:
            edges[info[1]].append(info[0])
        
        def dfs(node):
            nonlocal invalid
            # 将节点标记为 搜索中
            visited[node] = 1
            for v in edges[node]:
                # 如果 未搜索 ，那么搜索相邻节点
                if visited[v] == 0:
                    dfs(v)
                    if invalid:
                        return
                # 如果 搜索中 说明找到了环
                elif visited[v] == 1:
                    invalid = True
                    return
            # 将节点标记为 已完成
            visited[node] = 2
            # 将节点入栈
            res.append(node)
        # 每次挑选一个 未搜索 的节点，开始进行深度优先搜索
        for i in range(numCourses):
            if not invalid and not visited[i]:
                dfs(i)
        if invalid:
            return []
        # 如果没有环，那么就有拓扑排序
        # 注意下标 0 为栈底，因此需要将数组反序输出
        return res[::-1]

思路2:
参考官方思路:广度优先搜索。
思路一的深度优先搜索是一种「逆向思维」：最先被放入栈中的节点是在拓扑排序中最后面的节点。也可以使用正向思维，顺序地生成拓扑排序，这种方法也更加直观。
考虑拓扑排序中最前面的节点，该节点一定不会有任何入边，也就是它没有任何的先修课程要求。当将一个节点加入答案中后，就可以移除它的所有出边，代表着它的相邻节点少了一门先修课程的要求。如果某个相邻节点变成了「没有任何入边的节点」，那么就代表着这门课可以开始学习了。按照这样的流程，不断地将没有入边的节点加入答案，直到答案中包含所有的节点（得到了一种拓扑排序）或者不存在没有入边的节点（图中包含环）。
上面的想法类似于广度优先搜索，因此可以将广度优先搜索的流程与拓扑排序的求解联系起来。

算法步骤：
使用一个队列来进行广度优先搜索。初始时，所有入度为 $0$ 的节点都被放入队列中，它们就是可以作为拓扑排序最前面的节点，并且它们之间的相对顺序是无关紧要的。

在广度优先搜索的每一步中，取出队首的节点 $u$：

• 将 $u$放入答案中；
• 移除 $u$ 的所有出边，也就是将 $u$ 的所有相邻节点的入度减少 $1$。如果某个相邻节点 $v$ 的入度变为 $0$，那么就将 $v$放入队列中。

在广度优先搜索的过程结束后。如果答案中包含了这 $n$ 个节点，那么就找到了一种拓扑排序，否则说明图中存在环，也就不存在拓扑排序了。

参考图示:




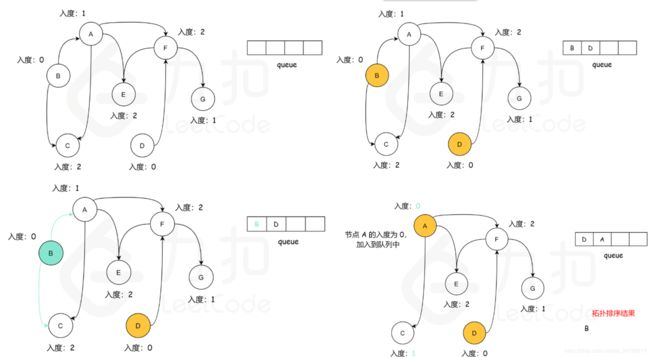
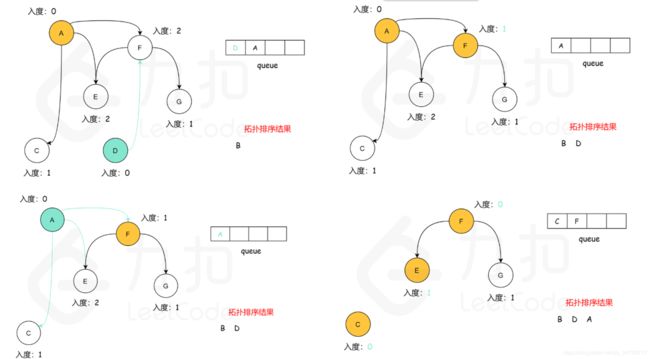
复杂度分析:
时间复杂度: $O(n+m)$，其中 $n$ 为课程数，$m$ 为先修课程的要求数。这其实就是对图进行广度优先搜索的时间复杂度。
空间复杂度: $O(n+m)$。题目中是以列表形式给出的先修课程关系，为了对图进行广度优先搜索，需要存储成邻接表的形式，空间复杂度为 $O(m)$。在广度优先搜索的过程中，需要最多 $O(n)$ 的队列空间（迭代）进行广度优先搜索，并且还需要若干个 $O(n)$ 的空间存储节点入度、最终答案等。

C++

class Solution {
private:
    vector<vector<int>> edges; // 存储有向图
    vector<int> indeg; // 存储每个节点的入度
    vector<int> res; // 存储答案
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        edges.resize(numCourses); // 初始化
        indeg.resize(numCourses);
        for( auto& info : prerequisites){
            edges[info[1]].push_back(info[0]); // 创建图
            ++indeg[info[0]]; // 入度加1
        }
        queue<int> q_node; // 节点队列
        // 将所有入度为0的节点放入队列中
        for(int i = 0; i < numCourses; ++i){
            if(indeg[i]==0) q_node.push(i);
        }
        // BFS遍历查找
        while(!q_node.empty()){
            int u = q_node.front(); // 队首取出一个元素
            q_node.pop(); 
            res.push_back(u); // 放入答案
            for(auto v : edges[u]){
                --indeg[v]; // 入度减一
                // 如果相邻节点 v 的入度为 0，就可以选 v 对应的课程了
                if(indeg[v] == 0) q_node.push(v);
            }
        }
        if(res.size() != numCourses) return {}; // 有环
        
        return res;
        
    }
};

Python:

class Solution:
    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        edges = collections.defaultdict(list) # 存储有向图
        indeg = [0] * numCourses # 存储每个节点的入度
        res = [] # 存储答案
        
        for info in prerequisites:
            edges[info[1]].append(info[0]) # 创建有向图
            indeg[info[0]] += 1 # 入度加1
        # 将所有入度为 0 的节点放入队列中
        q = collections.deque([u for u in range(numCourses) if indeg[u] == 0]) 
        
        while q:
            u = q.popleft() # 从队首取出一个节点
            res.append(u)  # 放入答案中
            
            for v in edges[u]:
                indeg[v] -= 1
                # 如果相邻节点 v 的入度为 0，就可以选 v 对应的课程了
                if indeg[v] == 0:
                    q.append(v)
        
        if len(res) != numCourses: return [] # 有环
        
        return res