斯坦福机器学习笔记（七）——高斯混合模型与EM算法

前记

博客的PDF资源已经上传CSDN，如有需要移步：GMM与EM算法 。GMM模型的Python代码请移步：利用Python实现高斯混合模型（GMM）

---

一 高斯混合模型

我们给定一个训练集$\left\{x^{\left(1\right)},\cdots ,x^{\left(m\right)}\right\}$ ，由于是高斯混合模型（Mixtures of Gaussians ，GMM）属于无监督算法，因此训练集中不会出现任何标签。

我们希望通过指定联合分布$p\left(x^{\left(i\right)},z^{\left(i\right)}\right)=p\left(x^{\left(i\right)}|z^{\left(i\right)}\right)p\left(z^{\left(i\right)}\right)$来对数据进行建模。在这里我们假定$z^{\left(i\right)}\sim Multinomial\left(\varphi \right)$ ，即 $z^{\left(i\right)}$ 服从多项式分布，${\varphi }_j\ge 0$ ，${\sum }_{j=1}^k{\varphi }_j=1$ ，并且参数 能够推导出 ，同时我们假设 ，在上叙述中， 代表 的种类数。因此，我们的模型假定每个 是通过从 中随机选择 而生成的，然后 也是来自依赖于 的 个高斯分布。那么上述模型被称为高斯混合模型。在这里， 是隐式随机变量，这也将我们估计问题变得非常困难。

那么对于给定的数据集$\left\{x^{\left(1\right)},\cdots ,x^{\left(m\right)}\right\}$ ，高斯混合模型的对数似然函数如下：
$$\begin{array}{rl}\ell (\varphi ,\mu ,\Sigma )& =\sum _{i=1}^m\log p\left(x^{(i)}|z^{(i)};\varphi ,\mu ,\Sigma \right)\\ & =\sum _{i=1}^m\log p\left(x^{(i)}|z^{(i)};\mu ,\Sigma \right)p\left(z^{(i)};\varphi \right)\end{array}$$
然而，如果我们令上述函数的偏导数为0的话，那么在封闭区域内，我们无法直接解决这个问题。

随机变量$z^{\left(i\right)}$ 表示每个$x^{\left(i\right)}$ 属于$k$ 个高斯分布的概率大小。请注意，如果我们知道$z^{\left(i\right)}$ 是多少，那么最大似然问题就很容易了。 具体来说，我们可以将对数似然函数写成：
$$\begin{array}{r}\ell \left(\varphi ,\mu ,\Sigma \right)=\sum _{i=1}^m\log p\left(x^{\left(i\right)}|z^{\left(i\right)};\mu ,\Sigma \right)\text{+}\log p\left(z^{\left(i\right)};\varphi \right)\end{array}$$
由于$z^{\left(i\right)}\sim Multinomial\left(\varphi \right)$ ，那么我们有 :
$$\begin{array}{r}p\left(z^{\left(i\right)};\varphi \right)=\prod _{j=1}^{k}p\left(z^{\left(i\right)}=j;\varphi \right)=\prod _{j=1}^k{\varphi }_j^{1\left\{z^{\left(i\right)}=j\right\}}\end{array}$$
同理，因为$x^{\left(i\right)}|z^{\left(i\right)}\text{= }j\sim \mathcal{N}\left({\mu }_j{\Sigma }_j\right)$，那么我们有：
$$\begin{array}{rl}& p\left(x^{\left(i\right)}|z^{\left(i\right)};\mu ,\Sigma \right)=\prod _{j=1}^{k}p\left(x^{\left(i\right)}|z^{\left(i\right)}=j;\mu ,\Sigma \right)\\ & \begin{array}{ccccc}& & & & \end{array}=\prod _{j=1}^k{\left\{\frac{1}{{\left(2\pi \right)}^{\frac{n}{2}}{\left|{\Sigma }_j\right|}^{\frac{1}{2}}}\exp \left(\text{-}\frac{1}{2}{\left(x^{\left(i\right)}-u_j\right)}^T{\Sigma }^{-1}\left(x^{\left(i\right)}-u_j\right)\right)\right\}}^{1\left\{z^{\left(i\right)}=j\right\}}\end{array}$$
因此，对数似然函数可以写成：
$$\begin{array}{rl}\ell (\varphi ,\mu ,\Sigma )& =\sum _{i=1}^m\log p\left(x^{(i)};\mu ,\Sigma \right)+\log p\left(z^{(i)};\varphi \right)\\ & =\sum _{i=1}^m(\sum _{j=1}^{k}1\left\{z^{(i)}=j\right\}\left\{-\frac{1}{2}{\left(x^{(i)}-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x^{(i)}-{\mu }_j\right)-\frac{n}{2}\log 2\pi -\frac{1}{2}\log \left|{\Sigma }_j\right|\right\}\\ & =\sum _{i=1}^{k}1\left\{z^{(i)}=j\right\}\log {\varphi }_j\end{array}$$
那么，对${\mu }_j$ 求偏导有：
$$\begin{array}{r}\frac{\partial \ell }{\partial {\mu }_j}=\sum _{i=1}^{m}1\left\{z^{\left(i\right)}=j\right\}{\Sigma }_j^{-1}\left(x^{\left(i\right)}-{\mu }_j\right)=0\end{array}$$
由于${\Sigma }_j$是矩阵，那么：
$$\frac{\partial \ell }{\partial {\mu }_j}=\sum _{i=1}^{m}1\left\{z^{(i)}=j\right\}{\Sigma }_j^{-1}\left(x^{(i)}-{\mu }_j\right)=0$$
同理，对${\Sigma }_j$ 求偏导有：
$${\mu }_j=\frac{{\sum }_{i=1}^{m}1\left\{z^{(i)}=j\right\}{x}^{(i)}}{{\sum }_{i=1}^{m}1\left\{z^{(i)}=j\right\}}$$
其中用到了如下矩阵求导公式：
$$\frac{\partial \ell }{\partial {\Sigma }_j}=\sum _{i=1}^{m}1\left\{z^{(i)}=j\right\}\left\{\frac{1}{2}\left(x^{(i)}-{\mu }_j\right){\left(x^{(i)}-{\mu }_j\right)}^T{\Sigma }_j^{-2}-\frac{1}{2}{\Sigma }_j^{-1}\right\}=0$$
因此，
$$\{\begin{array}{l}\frac{\partial |\Sigma |}{\partial \Sigma }=|\Sigma |{\Sigma }^{-1}\\ \frac{\partial {\Sigma }^{-1}}{\partial \Sigma }={\Sigma }^{-2}\end{array}$$
由于${\sum }_{j=1}^k{\varphi }_j=1$ ，那么我们必须利用拉格朗日乘数法来求解 。因此构造如下函数：
$${\Sigma }_j=\frac{{\sum }_{i=1}^{m}1\left\{z^{(i)}=j\right\}\left(x^{(i)}-u_j\right){\left(x^{(i)}-u_j\right)}^T}{{\sum }_{i=1}^m{1}^{\prime }{z}^{(i)}=j\}}$$
那么分别对${\varphi }_j,\alpha$ 求偏导有:
$$f(z;\varphi ,\alpha )=\sum _{i=1}^m\sum _{j=1}^{k}1\left\{z^{(i)}=j\right\}\log {\varphi }_j+\alpha \left(1-\sum _{j=1}^k{\varphi }_j\right)$$
那么我们可以得到：
$$\{\begin{array}{c}\frac{\partial f}{\partial {\varphi }_j}={\sum }_{i=1}^m\frac{1\left\{z^{(i)}=j\right\}}{{\varphi }_j}-\alpha =0\\ \frac{\partial f}{\partial \alpha }=1-{\sum }_{j=1}^k{\varphi }_j=0\end{array}$$
带入上式有：
$${\varphi }_j=\frac{1}{\alpha }\sum _{i=1}^{m}1\left\{z^{(i)}=j\right\}$$
那么有：
$$\sum _{j=1}^k{\varphi }_j=\sum _{j=1}^k\frac{1}{\alpha }\sum _{i=1}^{m}1\left\{z^{(i)}=j\right\}=\frac{1}{\alpha }\sum _{i=1}^m\sum _{j=1}^{k}1\left\{z^{(i)}=j\right\}=\frac{1}{\alpha }\sum _{i=1}^{m}1=\frac{m}{\alpha }=1$$
那么有：
$$\{\begin{array}{c}\alpha =m\\ {\varphi }_j=\frac{1}{m}{\sum }_{i=1}^{m}1\left\{z^{(i)}=j\right\}\end{array}$$
实际上，我们可以从上得知，如果$z^{\left(i\right)}$ 是已知的，那么高斯混合模型的最大似然估计变得几乎与我们在估计高斯判别分析模型的参数时所具有的相同，除了这里$z^{\left(i\right)}$正在起到类标签的作用。

然而，在我们的密度估计问题中， $z^{\left(i\right)}$是未知的。我们可以做什么？

EM算法是一种迭代算法，有两个主要步骤。 应用于我们的问题，在E步骤中，它试图“猜测$z^{\left(i\right)}$ 的值。在M步骤中，它根据我们的猜测更新模型的参数。 由于在M步骤中我们假设第一部分中的猜测是正确的，因此最大化变得容易。 下面是高斯混合模型的EM算法的伪代码：

在E步骤中，给定 $x^{\left(i\right)}$并使用当前设置的参数最后结合贝叶斯准则，我们计算得到参数$z^{\left(i\right)}$ 的后验概率：
$$\begin{array}{r}p\left(z^{\left(i\right)}=j|x^{\left(i\right)},;\varphi ,\mu ,\Sigma \right)=\frac{p\left(x^{\left(i\right)}|z^{\left(i\right)}=j;\mu ,\Sigma \right)p\left(z^{\left(i\right)}=j;\varphi \right)}{\sum _{l=1}^{k}p\left(x^{\left(i\right)}|z^{\left(i\right)}=l;\mu ,\Sigma \right)p\left(z^{\left(i\right)}=l;\varphi \right)}\end{array}$$

在这里，$p\left(x^{\left(i\right)}|z^{\left(i\right)}=j;\mu ,\Sigma \right)$ 由样本$x^{\left(i\right)}$在均值为${\mu }_j$ ，协方差矩阵为${\Sigma }_j$ 的高斯分布上的概率给出；同时， $p\left(z^{\left(i\right)}=j;\varphi \right)$由${\varphi }_j$给出。在E步骤中计算的$w_j^{\left(i\right)}$的值表示我们对$z^{\left(i\right)}$ 的“软”猜测。

此外，通过将M步骤中的参数更新与我们确切知道$z^{\left(i\right)}$ 时的公式进行对比，你可以发现它们是相同的，除了没有表明每个数据点来自哪个高斯分布的指示函数$1\left\{z^{\left(i\right)}=j\right\}$ ，而我们现在将其改为

---

二 Jessen不等式

为了更好地理解EM算法的原理，我们必须对子EM算法中运用广泛的Jessen不等式进行详细推导。

设$f$ 是一个定义域为实数集的函数。回想一下，如果$\forall x\in R,f^{\prime \prime }\left(x\right)\ge 0$ ，那么$f$ 是一个凸函数。当对于$f$ 的向量输入，这是广义的条件，它的海森$H$（hessian）矩阵 是半正定，即$H\ge 0$ 。如果$\forall x\in R,f^{\prime \prime }\left(x\right)>0$ ，那么我们说$f$是严格凸函数(在向量值情况下，相应的表述为$H$必须是严格的半正定的，记为$H>0$ 。

那么Jessen不等式可以这样表述为： $f$是凸函数，即$\forall x\in R,f^{\prime \prime }\left(x\right)>0$ ，假定$X$ 是随机变量，那么有$E\left[f\left(X\right)\right]\ge f\left(EX\right)$ 。而且，如果$f$是严格凸函数时，那么当且仅当$p\left(X=E\left[X\right]\right)=1$ 时， $E\left[f\left(X\right)\right]\ge f\left(EX\right)$ (即当$X$ 是常数时)，其中， $E\left(X\right)$代表随机变量 的数学期望。其实这是Jessen不等式的一般形式，Jessen不等式的加权形式为：$\forall x\in R,f^{\prime \prime }\left(x\right)\ge 0,q_1,\cdots ,q_n\in {\mathbb{R}}^{+},\sum _{i=1}^n{q}_n=1$ ，那么$\sum _{i=1}^n{q}_{i}f\left(x_i\right)\ge f\left(\sum _{i=1}^n{q}_i{x}_i\right)$ 恒成立。同理，如果当$f$是个凹函数时，Jessen不等式的一般形式为：$\forall x\in R,f^{\prime \prime }\left(x\right)\le 0$ ，假定$X$ 是随机变量，那么有$E\left[f\left(X\right)\right]\le f\left(EX\right)$ 。其加权形式为：$\forall x\in R,f^{\prime \prime }\left(x\right)\le 0,q_1,\cdots ,q_n\in {\mathbb{R}}^{+},\sum _{i=1}^n{q}_n=1$ ，那么$\sum _{i=1}^n{q}_{i}f\left(x_i\right)\le f\left(\sum _{i=1}^n{q}_i{x}_i\right)$ 恒成立。下面对利用数学归纳法来证明Jessen不等式。

我们以$f$是凸函数为例来证明Jessen不等式的加权形式。证明过程如下：

1. 当$n=1$时，$q_1=1$，那么$q_{1}f\left(x_1\right)=f\left(x_1\right)=f\left(q_1{x}_1\right)$ 恒成立。
2. 当$n=2$时，$q_1+q_2=1$ ，由于$f^{\prime \prime }\left(x\right)\ge 0$ ，那么根据不等式性质我们有: $q_{1}f\left(x_1\right)\text{+}{q}_{2}f\left(x_2\right)\ge f\left(q_1{x}_1+q_2{x}_2\right)$恒成立。
3. 当$n\ge 3$时，假设当 $n=k$时 $\sum _{i=1}^k{q}_{i}f\left(x_i\right)\le f\left(\sum _{i=1}^n{q}_i{x}_i\right)$恒成立，那么只需证明，当 $n=k+1$ 时，$\sum _{i=1}^{k+1}{q}_{i}f\left(x_i\right)\le f\left(\sum _{i=1}^n{q}_i{x}_i\right)$ 。那么$\forall x\in R,f^{\prime \prime }\left(x\right)\ge 0,q_1,\cdots ,q_{k+1}\in {\mathbb{R}}^{+},\sum _{i=1}^{k+1}{q}_n=1$ 时，显然有：
   $$\begin{array}{rl}& \sum _{i=1}^{k+1}{q}_{i}f\left(x_i\right)\text{=}{q}_{k+1}f\left(x_{k\text{+}1}\right)\text{+}\sum _{i=1}^k{q}_{i}f\left(x_i\right)\text{=}{q}_{k+1}f\left(x_{k\text{+}1}\right)\text{+}{\text{z}}_k\sum _{i=1}^k\frac{q_i}{{\text{z}}_k}f\left(x_i\right)\left(z_k=\sum _{i=1}^k{q}_i\right)\\ & \begin{array}{cccc}& & & \ge q_{k+1}f\left(x_{k\text{+}1}\right)\end{array}+{\text{z}}_{k}f\left(\sum _{i=1}^k\frac{q_i}{{\text{z}}_k}{x}_i\right)\\ & \begin{array}{cccc}& & & \ge \end{array}f\left(q_{k+1}{x}_{k\text{+}1}+{\text{z}}_k\sum _{i=1}^k\frac{q_i}{{\text{z}}_k}{x}_i\right)=f\left(\sum _{i=1}^{k+1}{q}_i{x}_i\right)\end{array}$$
   综合1)、2)、3)有，Jessen不等式恒成立。同理可证$f$ 是凹函数时的Jessen不等式恒成立。
   

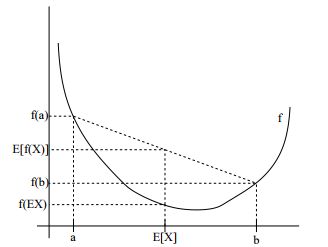
为了更好地理解Jessen不等式，我们来看上面的函数图。在图中，$f$是由实线表示的凸函数。 $X$是随机变量，各有0.5的概率取得变量$a$和变量$b$。因此，$X$的期望值由$a$和$b$之间的中点给出。我们还可以看到$f\left(a\right)$ ，$f\left(b\right)$和$f\left(E\left[X\right]\right)$在$y$轴上的值。 $E\left[f\left(X\right)\right]$现在是$f\left(a\right)$和$f\left(b\right)$ 之间的中点。从我们的例子中,我们看到，因为$f$是凸函数， $E\left[f\left(X\right)\right]\ge f\left(EX\right)$恒成立。

因此，Jessen不等式也可以这样理解，当指定函数是凸函数时，函数值的加权平均大于等于自变量的加权平均后对应的函数值；当指定函数是凹函数时，函数值的加权平均小于等于自变量的加权平均后对应的函数值。

---

三 EM算法

假设我们有一个评估问题，其中有一个训练集$\left\{x^{\left(i\right)},\cdots ,x^{\left(m\right)}\right\}$ 由$m$个独立的样本组成。我们希望利用数据来你拟合模型$p\left(x,z\right)$ 的参数，其中似然函数为：
$$\begin{array}{r}\ell \left(\theta \right)=\sum _{i=1}^m\log p\left(x;\theta \right)=\sum _{i=1}^m\log \sum p\left(x,z;\theta \right)\end{array}$$
但是，明显寻找参数$\theta $ 极大似然估计是困难的。这里$z^{\left(i\right)}$ 是隐式随机变量；通常情况下，若果知道了$z^{\left(i\right)}$ ，那么极大似然估计就会很容易。

在这种情况下，EM算法给出了一种有效的估计最大值似然的方法.最大化 $\ell \left(\theta \right)$明显可能很困难，我们的策略是重复构造一个上确界(E-step)，然后优化这个上下限(M-step)。

对于每一个 ，令$Q_i$是$z$的函数，且有 ${\sum }_z{Q}_i\left(z\right)=1$，$Q_i\left(z\right)\ge 0$ 。那么根据Jessen不等式，我们有：
$$\begin{array}{rl}\sum _i\log p\left(x^{(i)};\theta \right)& =\sum _i\log \sum p\left(x^{(i)},z;\theta \right)\\ & =\sum _i\log \sum _{z^{\prime \prime }}{Q}_i\left(z^{(i)}\right)\frac{p\left(x^{(i)},z^{(i)};\theta \right)}{Q_i\left(z^{(i)}\right)}\\ & \ge \sum _i\sum _{z^{\prime }}{Q}_i\left(z^{(i)}\right)\log \frac{p\left(x^{(i)},z^{(i)};\theta \right)}{Q_i\left(z^{(i)}\right)}\end{array}$$
具体地说, $f\left(x\right)=\log x=\ln x$是凹函数,因为$\forall x\in {\mathbb{R}}^{+},f^{\prime \prime }\left(x\right)=\text{-}\frac{1}{x^2}<0$ 。

现在，对于任何一组分布$Q_i$ ，公式(3)为$\ell \left(\theta \right)$ 给出了一个下界。 $Q_i$ 有很多可能的选择。我们应该用哪一种？如果我们有一些目前想猜测的参数 $\theta$，很自然地让似然函数在$\theta$ 处的下界变小是我们的目标。即我们将使上面的不等式在$\theta$ 处等号成立。

为了一个特殊$\theta$ 是的上界变小，我们的推动过程中需要涉及Jessen不等式去等的条件。为了使等号成立，我们知道期望是常变量时将会带来高效率。即我们要求：
$$\begin{array}{r}\frac{p\left(x^{\left(i\right)},z^{\left(i\right)};\theta \right)}{Q_i\left(z^{\left(i\right)}\right)}\text{=}c\end{array}$$
对于不依赖于$z^{\left(i\right)}$ 的常数$c$ ，只要满足$Q_i\left(z^{\left(i\right)}\right)\propto p\left(x^{\left(i\right)},z^{\left(i\right)};\theta \right)$如下条件即可。实际上，由于${\sum }_z{Q}_i\left(z^{\left(i\right)}\right)=1$ ，那么我们有：
$$\begin{array}{rl}{Q}_i\left(z^{(i)}\right)& =\frac{p\left(x^{(i)},z^{(i)};\theta \right)}{{\sum }_{z}p\left(x^{(i)},z;\theta \right)}=\frac{p\left(x^{(i)},z^{(i)};\theta \right)}{p\left(x^{(i)};\theta \right)}\\ & =p\left(z^{(i)}|x^{(i)};\theta \right)\end{array}$$
因此，我们只是将$Q_i$设置为$z^{\left(i\right)}$ 的后验分布，$z^{\left(i\right)}$是$x^{\left(i\right)}$ 的条件概率，且被$\theta $ 参数化。

现在，对于$Q_i$ 的选择，式(1)给出了我们试图最大化的对数似然的下界，这是E步骤。算法的M步骤中，最大化式(1)的参数$\theta$ ，从而获得一个新参数 。反复执行这两个步骤。上述就是EM算法的两个过程，具体流程如下所示：

$$\begin{array}{rl}& Repeatuntilconvergence\{\\ & \begin{array}{ccc}& & \end{array}\left(E\text{-}Step\right)Foreachi,set\\ & \begin{array}{cccc}& & & \end{array}\begin{array}{cccc}& & & \end{array}{Q}_i\left(z^{\left(i\right)}\right)=p\left(z^{\left(i\right)}|x^{\left(i\right)};\theta \right)\\ & \begin{array}{ccc}& & \end{array}\left(M-step\right)Set\\ & \begin{array}{cccc}\begin{array}{cccc}& & & \end{array}& & & \end{array}\theta :=arg\underset{\theta }{\max }\sum _i\sum _{z^{\left(i\right)}}{Q}_i\left(z^{\left(i\right)}\right)\log \frac{p\left(x^{\left(i\right)},z^{\left(i\right)};\theta \right)}{Q_i\left(z^{\left(i\right)}\right)}\\ & \end{array}$$

我们怎么知道EM是否收敛？假设${\theta }^{\left(t\right)}$ 和${\theta }^{\left(t+1\right)}$ 连续两次迭代的参数。接下来我们将证明$\ell \left({\theta }^{\left(t\right)}\right)\le \ell \left({\theta }^{\left(t+1\right)}\right)$，这也将解释EM为什么总是单调提高对数似函数。这个结果的关键在于我们对${{Q}_{i}}$的选择。具体来说，在EM算法的迭代过程中，参数将从开始${\theta }^{\left(t\right)}$ ，那么我们令$Q_i^{\left(t\right)}\left(z^{\left(i\right)}\right)=p\left(z^{\left(i\right)}|x^{\left(i\right)};{\theta }^{\left(t\right)}\right)$ 。我们在前面看到，这个选择确保了Jensen不等式能够取等。因此：

$$\begin{array}{rl}& \ell \left({\theta }^{\left(t+1\right)}\right)\ge \sum _i\sum _{z^{\left(i\right)}}{Q}_i^{\left(t\right)}\left(z^{\left(i\right)}\right)\log \frac{p\left(x^{\left(i\right)},z^{\left(i\right)};{\theta }^{\left(t+1\right)}\right)}{Q_i^{\left(t\right)}\left(z^{\left(i\right)}\right)}\\ & \begin{array}{ccc}& & \ge \end{array}\sum _i\sum _{z^{\left(i\right)}}{Q}_i^{\left(t\right)}\left(z^{\left(i\right)}\right)\log \frac{p\left(x^{\left(i\right)},z^{\left(i\right)};{\theta }^{\left(t\right)}\right)}{Q_i^{\left(t\right)}\left(z^{\left(i\right)}\right)}\\ & \begin{array}{ccc}& & =\end{array}\ell \left({\theta }^{\left(t\right)}\right)\end{array}$$

那么，令$Q_i\text{=}{Q}_i^{\left(t\right)}$ ，$\theta \text{=}{\theta }^{\left(t\text{+}1\right)}$。为了得到式(2)，我们令
$$\begin{array}{r}{\theta }^{\left(t\text{+}1\right)}\text{=}arg\underset{\theta }{\max }\sum _i\sum _{z^{\left(i\right)}}{Q}_i\left(z^{\left(i\right)}\right)\log \frac{p\left(x^{\left(i\right)},z^{\left(i\right)};\theta \right)}{Q_i\left(z^{\left(i\right)}\right)}\end{array}$$
因此，在$\theta \text{=}{\theta }^{\left(t\text{+}1\right)}$ 处，该公式必须等于或大于在${\theta }^{\left(t\right)}$ 处的。

因此，EM是的似然函数单调收敛。在我们的EM算法的编写，我们说我们运行它直到收敛。鉴于我们刚刚展示的结果，一个合理的收敛性测试检查是连续迭代之间 $\ell \left(\theta \right)$之间的误差是否小于一些容差参数，如果 $\ell \left(\theta \right)$改进过慢，那么我们说EM算法收敛。
那么如果我们定义如下函数：
$$\begin{array}{r}J\left(Q,\theta \right)=\sum _i\sum _{z^{\left(i\right)}}{Q}_i\left(z^{\left(i\right)}\right)\log \frac{p\left(x^{\left(i\right)},z^{\left(i\right)};\theta \right)}{Q_i\left(z^{\left(i\right)}\right)}\end{array}$$

从之前推导可以得知$\ell \left(\theta \right)\ge J\left(Q,\theta \right)$ 。那么EM算法也可以看成通过不断迭代， $J\left(Q,\theta \right)$不断逼近$\ell \left(\theta \right)$ 的过程，其中E步骤是最大化$Q$（自我检查），然后M步骤就是最大化$\theta$ 。具体示意图如下所示。

---

四 再看高斯混合模型

根据我们对EM算法的一般定义，让我们回到我们在高斯混合中拟合参数 $\varphi$，$\mu$和$\Sigma$的旧例子上。
E步骤很简单。按照上面的算法推导，我们简单地令，
$$\begin{array}{r}{w}_j^{\left(i\right)}=Q_i\left(z^{\left(i\right)}=j\right)=p\left(z^{\left(i\right)}=j|x^{\left(i\right)};\varphi ,\mu ,\Sigma \right)\end{array}$$
这里，$Q_i\left(z^{\left(i\right)}=j\right)$表示在分布$Q_i$下$z^{\left(i\right)}=j$的概率。
接下来是M步骤，我们需要最大化参数 $\varphi$ ，$\mu$和$\Sigma$。首先我们化简似然函数。其过程如下：
$$\begin{array}{rl}& \ell \left(\varphi ,\mu ,\Sigma \right)=\sum _{i=1}^m\sum _{z^{\left(i\right)}}{Q}_i\left(z^{\left(i\right)}\right)\log \frac{p\left(x^{\left(i\right)},z^{\left(i\right)};\varphi ,\mu ,\Sigma \right)}{Q_i\left(z^{\left(i\right)}\right)}\\ & \begin{array}{cc}& \end{array}=\sum _{i=1}^m\sum _{j=1}^k{Q}_i\left(z^{\left(i\right)}=j\right)\log \frac{p\left(x^{\left(i\right)}|z^{\left(i\right)}=j;\mu ,\Sigma \right)p\left(z^{\left(i\right)}=j;\varphi \right)}{Q_i\left(z^{\left(i\right)}=j\right)}\\ & \begin{array}{cc}& \end{array}=\sum _{i=1}^m\sum _{j=1}^k{w}_j^{\left(i\right)}\log \frac{\frac{1}{{\left(2\pi \right)}^{\frac{n}{2}}{|{\Sigma }_j|}^{\frac{1}{2}}}\exp \left(\text{-}\frac{1}{2}{\left(x^{\left(i\right)}-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x^{\left(i\right)}-{\mu }_j\right)\right){\varphi }_j}{w_j^{\left(i\right)}}\\ & \begin{array}{cc}& \end{array}\text{=}\sum _{i=1}^m\sum _{j=1}^k{w}_j^{\left(i\right)}\left(\text{-}\frac{n}{2}\log 2\pi -\frac{1}{2}\log \left|{\Sigma }_j\right|+\log {\varphi }_j-\log w_j^{\left(i\right)}-\frac{1}{2}{\left(x^{\left(i\right)}-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x^{\left(i\right)}-{\mu }_j\right)\right)\end{array}$$

那么首先最大化${\mu }_j$，$\ell \left(\varphi ,\mu ,\Sigma \right)$对${\mu }_j$求偏导有：
$$\begin{array}{rl}& \frac{\partial \ell }{\partial {\mu }_j}=\frac{\partial }{\partial {\mu }_j}\sum _{i=1}^m\sum _{j=1}^k{w}_j^{\left(i\right)}\left(\text{-}\frac{n}{2}\log 2\pi -\frac{1}{2}\log \left|{\Sigma }_j\right|+\log {\varphi }_j-\log w_j^{\left(i\right)}-\frac{1}{2}{\left(x^{\left(i\right)}-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x^{\left(i\right)}-{\mu }_j\right)\right)\\ & \begin{array}{cc}& \end{array}=-\sum _{i=1}^m\frac{1}{2}{w}_j^{\left(i\right)}{\left(x^{\left(i\right)}-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x^{\left(i\right)}-{\mu }_j\right)\\ & \begin{array}{cc}& \end{array}=\sum _{i=1}^m{w}_j^{\left(i\right)}{\Sigma }_j^{-1}\left(x^{\left(i\right)}-{\mu }_j\right)\end{array}$$
那么令上式等于0有：
$$\begin{array}{r}{\mu }_j=\frac{\sum _{i=1}^m{w}_j^{\left(i\right)}{x}^{\left(i\right)}}{\sum _{i=1}^m{w}_j^{\left(i\right)}}\end{array}$$
同理，接下来最大化${\Sigma }_j$，$\ell \left(\varphi ,\mu ,\Sigma \right)$对${\Sigma }_j$求偏导有：
$$\begin{array}{rl}& \frac{\partial \ell }{\partial {\Sigma }_j}=\frac{\partial }{\partial {\Sigma }_j}\sum _{i=1}^m\sum _{j=1}^k{w}_j^{\left(i\right)}\left(\text{-}\frac{n}{2}\log 2\pi -\frac{1}{2}\log \left|{\Sigma }_j\right|+\log {\varphi }_j-\log w_j^{\left(i\right)}-\frac{1}{2}{\left(x^{\left(i\right)}-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x^{\left(i\right)}-{\mu }_j\right)\right)\\ & \begin{array}{cc}& \end{array}=-\sum _{i=1}^m\frac{1}{2}{w}_j^{\left(i\right)}{\left(x^{\left(i\right)}-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x^{\left(i\right)}-{\mu }_j\right)-\sum _{i=1}^m\frac{1}{2}\log \left|{\Sigma }_j\right|\\ & \begin{array}{cc}& \end{array}=-\frac{1}{2}\sum _{i=1}^m{w}_j^{\left(i\right)}\left[{\Sigma }_j^{-1}-{\Sigma }_j^{-2}\left(x^{\left(i\right)}-{\mu }_j\right){\left(x^{\left(i\right)}-{\mu }_j\right)}^T\right]\end{array}$$
那么令上式等于0，我们有：
$$\begin{array}{r}{\Sigma }_j=\frac{\sum _{i=1}^m{w}_j^{\left(i\right)}\left(x^{\left(i\right)}-{\mu }_j\right){\left(x^{\left(i\right)}-{\mu }_j\right)}^T}{\sum _{=1}^m{w}_j^{\left(i\right)}}\end{array}$$
最后我们利用拉格朗日乘数法来最大化${\varphi }_j$。由于$\sum _{j=1}^k{\varphi }_j=1$，那么我们根据上述似然函数构造如下函数：
$$\begin{array}{r}\mathcal{L}\left(\varphi \right)=\sum _{i=1}^m\sum _{j=1}^k{w}_j^{\left(i\right)}\log {\varphi }_j+\beta \left(1-\sum _{j=1}^k{\varphi }_j\right)\end{array}$$
因此我们有：
$$\begin{array}{rl}& \frac{\partial \mathcal{L}}{\partial {\varphi }_j}=\sum _{i=1}^m\frac{w_j^{\left(i\right)}}{{\varphi }_j}-\beta =0\\ & \frac{\partial \mathcal{L}}{\partial \beta }=1-\sum _{j=1}^k{\varphi }_j=0\end{array}$$
由于$\sum _{j=1}^k{w}_j^{\left(i\right)}=1$，那么可以求得：
$$\begin{array}{r}{\varphi }_j=\frac{1}{m}\sum _{i=1}^m{w}_j^{\left(i\right)}\end{array}$$

---

对于高斯混合模型(GMM)的个人理解：GMM就是首先假设 个分类，且每个分类服从于不同的高斯分布，且这 个不同的高斯分布的协方差矩阵完全相同。并且给这些高斯分布不同的初始概率（权重）。之后通过EM算法进行跟新模型的所有参数直至似然函数收敛。最终每组数据的 个不同分类的概率，去除概率最大对应的类别作为预测分类。